since 2003 イレコナビ　サイトマップ
	< 学問 >
		< 活動報告 >
			< 学会発表 >
				< 日本物理学会2013年春季大会 >
					日本物理学会2013年春季大会での私の発表は、文法物理学についての27pRD-2「新文法版シュレディンガー方程式の古典力学描像」だけだった。 物理教育の会場での発表は、今回は、しなかった。 発表旅行中に撮影した写真は、私の写メール投稿ブログ「即達」の2013年03月部分に掲載されています。 私の発表についてのご意見ご感想はWooder!掲示板にお寄せ下さい。 今回は、忘れずに、ジュニアセッションを見学した。 会場で、私が、一瞬非常に不機嫌な表情に成ってしまったら、近くに居た人が、それを察知して、発表の仕方に注文を付けたのではないか、と思われる事があった。 普通に考えると、そんなのは気のせいなはずだが、私の場合、あながち、そういう事があっても不思議ではない、と思わせる様な事が、身の回りで色々と起こる。 私の意識は、大体いつも、外界に50%、内面に50%という風に向けられているので、表情は、外界に対する物ではない事が多い。 その時も、非常に腹立たしい事を白日夢の様に思い出してしまっていた。 発表に対して不満を持ったのではないので、発表した人には安心して欲しい。 発表に対しては、非常に優秀だ、と感じた。 その年齢だった頃の私よりも良く発達している部分を、発表した皆さんは持っている、と思った。 オリジナリティについては、良く分かりませんでしたし、もちろん要求してはいけないのですが、大人が発表したら認められるけど同じ事を子供が発表したら認められない、という事は、あってはいけないのだ、と思います。 心霊写真の原因が複屈折だ、というのは、発表を見るまで、私は知りませんでした。 コジツケてなくて非常に歯切れの良い説明だった、と思います。 発表者は、カメラの説明書には書かれていなかった、と発表していました。 私も、テレビで心霊写真が紹介された時に、複屈折の話を聞いた事はありません。 物理学としてのオリジナリティは無いかもしれませんが、しかし、それなら、私が子供の頃に耳目を集めた人工ヒトダマは物理学者による研究として何故あれだけ取り上げられたのか、という疑問が生じます。 その辺は、どうなのでしょうか？ RD会場は、広島大学東広島キャンパス理学研究科E棟2階E208教室だった。 自分の発表では、セッション開始前に鈴木さんと雑談しながら待機している時に、部屋の様子を見に来た座長さんに、寒いが暖房は入れてもらえないか訊くと、このセッションは30分間のセッションなので暖房は入れない、との事だった。 発言タイミング 発言内容 注釈 ohp13sp-sr-1 宜しくお願いします。 www.GrammaticalPhysics.acの宇田雄一です。 新文法版シュレディンガー方程式の古典力学描像について発表します。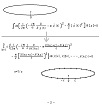 www.GrammaticalPhysics.ac www.GrammaticalPhysics.ac > Products of Grammatical Physics > Theory of Quantum History Entangled in Time-like Direction > Cartoon of the Equation ohp13sp-sr-2 新文法版シュレディンガー方程式というのは、日本物理学会2011年秋の大会の16pSC-2で私が発表した物で、その中の時間を円環時間にして、ポテンシャルの部分をゼロに置いた物が(ohp13sp-sr-2の最初の式を指して)これなんですが、この方程式を、どういう方程式なのか、こう見ても、ちょっと分かり難い、分かり難いと言っても、その時発表したのは、(ohp13sp-sr-2の最初の式中のmdχ(t)/dtを指して)ここがベクトルポテンシャルみたいだと、で、(ohp13sp-sr-2の最初の式中の-(m/2)[dχ(t)/dt]2を指して)ここが電磁場のスカラーポテンシャルみたいだ、(ohp13sp-sr-2の最初の式中のmdχ(t)/dtを指して)ここが電磁場のベクトルポテンシャルみたいな、そういう格好をしている、という事ですねえ。 エネルギー固有値ゼロの定常状態のシュレディンガー方程式みたいな形をしているけれど、もう少しちょっと具体的に分からないものか、という事で、この方程式の内容を漫画に描いてみたい、という、そういう発想なんですが、そのためにですねえ、まずはですねえ、(ohp13sp-sr-2の冒頭の図を指して)この時間を、連続の時間から(ohp13sp-sr-2の下の図を指して)離散の時間に変えてですね、ε刻みでの離散的な時間を考えます。 するとですねえ、(ohp13sp-sr-2の灰色の矢印の下の式を指して)この様にまあ書く事が出来るでしょう、という事ですねえ。 (ohp13sp-sr-2の最初の式中の積分記号のdtを指して)dtの部分を(ohp13sp-sr-2の灰色の矢印の下の式中のΣ記号の右隣のεを指して)εにしてですね、n個に分割した、という事ですねえ。 (ohp13sp-sr-2の最初の式中のδ/δχ(t)を指して)この汎関数微分の部分は、(ohp13sp-sr-2の灰色の矢印の下の式中の∂/∂χ(kε)を指して)偏微分に成ります。 (ohp13sp-sr-2の最初の式中のdχ(t)/dtを指して)この時間での微分の部分というのは、これは、(ohp13sp-sr-2の灰色の矢印の下の式中の[χ(kε+ε)-χ(kε)]/εを指して)時間の部分をε進めてεで割っておけば時間での微分みたいなもんでしょう、という事でね、そういう風にしました。 で、(ohp13sp-sr-2の最初の式中のΦを指して)これは、Φというのは、これは汎関数ですが、χという関数の汎関数ですが、この時間を離散化するとですね、χの定義域は、(ohp13sp-sr-2の冒頭の図を指して)この連続的な時間だったわけですが、時間を離散化すると、(ohp13sp-sr-2の最初の式中のΦを指して)このΦというのが、汎関数ではなくて、(ohp13sp-sr-2の灰色の矢印の下の式中のΦを指して)この様なn変数関数と考える事が出来るでしょう、という事なんですね。 そして、これの漫画を描いて行きたい、という事なんですが、 日本物理学会2011年秋季大会＠学会発表＠活動報告 円環時間については、日本物理学会2009年秋季大会＠学会発表＠活動報告に、書かれています。 「時間の部分をε進めてεで割っておけば」は少し間違った言い方です。 「時間の部分をε進めて差を取ってεで割っておけば」と言うべきでした。 ohp13sp-sr-3 漫画という事で、かなり乱暴なんですがn, 分割する個数、を3にまで減らしてしまいました。 すると、さっきの方程式は、(ohp13sp-sr-3の冒頭の式を指して)この様に、かなり短く成ります。 と言っても、まあ、シグマを使って書いてるから、ほとんど短くは成ってないんですが。 これを具体的に書くとですね、(ohp13sp-sr-3の後半の式を指して)この様に、nが3だったら、分割する個数が3だったら、何とか書けてしまう。 これが、講演概要に書いてある式です。 - ohp13sp-sr-4 で、この式は何かと言いますとですねえ、(ohp13sp-sr-4の3行目の式を指して)mεα2をMと書いて、mをQと書いて、Mが質量でQが電荷の様に見ると、さらにですね、(ohp13sp-sr-4の2行目の式を指して)この変数をですね、χ(ε)とかχ(2ε),χ(3ε)をx1,x2,x3と置く事にしました。 これちょっとχ1,χ2,χ3に成っておりますが、x1,x2,x3と書きたかったんですけど、間違ってχに成っております。 でですねえ、円環時間だから、(ohp13sp-sr-4の2行目のχ(ε)とχ(4ε)を指して)このχ(ε)とχ(4ε)は同じです。 という事で、3次元空間中の荷電粒子の量子力学みたいな物に成ります。 (ohp13sp-sr-4の4行目の式を指して)偏微分は、これはまあ、初等的な量子力学に出て来る運動量演算子の座標表示と同じですから、(ohp13sp-sr-4の2行目から4行目までの式を指して)変数の置き方、x1,x2,x3,M,Qそれからp1,p2,p3というものを、この様に置いて、さらに、(ohp13sp-sr-4の5行目から8行目までの式を指して)このA1,A2,A3という関数とφという関数を、この様に書くと、そうすると、今4ページ目ですが、3ページ目に書いてあった、講演概要に出てる式はこれです、と言った物は、4ページ目の一番上の、(ohp13sp-sr-4の1行目の式を指して)この式に、まとまります。 で、これは、初等的な量子力学のハミルトニアンですねえ。 という事でですねえ、最初に出て来た、この方程式の漫画を描きたい、という漫画は何かと言うと、(ohp13sp-sr-4の1行目の式を指して)この方程式が量子力学のハミルトニアンである様な系の古典力学なんですが、それを最初に出て来た方程式の漫画と思いましょう、という事で。 そうすると、その古典力学系というのはどんな物か、と言いますと、ベクトルポテンシャルが(ohp13sp-sr-4の5行目から7行目までの式を指して)こうでスカラーポテンシャルが(ohp13sp-sr-4の8行目の式を指して)こうである様な電磁場中を運動する(ohp13sp-sr-4の3行目の式を指して)電荷がQ, 質量がMの荷電粒子である、という事に成ります。 で、ベクトルポテンシャルが(ohp13sp-sr-4の5行目から7行目までの式を指して)これでスカラーポテンシャルが(ohp13sp-sr-4の8行目の式を指して)こうだと、磁場の方が(ohp13sp-sr-4の9行目から11行目までの左半分の式を指して)こうで、電場の方が(ohp13sp-sr-4の9行目から11行目までの右半分の式を指して)こうです。 (ohp13sp-sr-4の9行目から11行目までの左半分の式を指して)これは、まあ、磁場と言わずに磁束密度と言うのか知らないけど、こう成りましてですね。 講演概要にもχ1,χ2,χ3と書いています。 これでは間違いだ、というわけではありません。 初等的な量子力学という表現の「初等的な」は余計だった。 新文法版の量子力学や相対論的量子力学や場の量子論との区別が念頭にあったからだと思うが、既存の量子力学、ないし、既存の非相対論的量子力学、と言えばよかった。 「・・・磁束密度と言うのか知らないけど」については、知らない事はないのだけど、それは磁場ではなくて磁束密度だ！という風にメクジラを立てるタイプの価値観に対する皮肉を込めて、そんな事どっちでも良いじゃないか、という価値観を表現するために、「知らないけど」という言い方をしました。 ohp13sp-sr-5 で、これを書き直すとですねえ、先ほどの、要するに、(ohp13sp-sr-4を再掲して)これは成分で書いたものですが、ベクトルポテンシャル、(ohp13sp-sr-4の5行目から7行目までの式を指して)これを∇×Aにすると、(ohp13sp-sr-4の9行目から11行目までの左半分の式を指して)このBが出て来ると、で、(ohp13sp-sr-4の8行目の式を指して)これをgradientを取ると(ohp13sp-sr-4の9行目から11行目までの右半分の式を指して)これが出て来る、という事ですが、これは成分で書いておりますが、これを、3次元ベクトルの記号で書くと、(ohp13sp-sr-5を掲示して)この様に成ります。 (ohp13sp-sr-5の1行目を指して)磁場がですねえ、i+j+kという方向を向いている一定の磁場です。 で、電場はですねえ、(ohp13sp-sr-5の2行目を指して)こんなに成るんですが、(ohp13sp-sr-5の3行目の左の式を指して)この単位ベクトルnと、(ohp13sp-sr-5の3行目の右の式を指して)これは位置ベクトルrというものを、これを使うとですねえ、(ohp13sp-sr-5の赤枠内の式を指して)この様に、電場の方も簡単に書けます。 で、(ohp13sp-sr-5の赤枠内の右の式を指して)これは何かと言うとですねえ、nという方向に対して垂直に成ってる、これは、高校数学のベクトルを考えれば良いと思いますが、これは、rというベクトルからnというベクトルに垂線を下ろした、その足からrの先端に向かう様なベクトルに成っておりますので、nというベクトルに垂直にnから発散する様な形の向きを向いている電場ですねえ、こっちはねえ。 そいで、(ohp13sp-sr-5の赤枠内の左の式を指して)こっちは、磁場は、nという方向に沿った磁場に成っております。 で、この中を運動する、具体的に質量M, さっきの(ohp13sp-sr-4の3行目の式を指して)これとですね、それから電荷Qを使って、古典力学の計算をすると、(ohp13sp-sr-5の赤枠内の式を指して)この磁場この電場の中を運動する荷電粒子は、どの様な運動が出て来たかと言うと、(ohp13sp-sr-5の赤枠の下の日本語の文章を指しながら)以下の運動に、z軸の方向をn軸の方向に重ねる様な回転を、(ohp13sp-sr-5の最後の3行の式を指して)この運動に施して得られる様な運動、だからまあ、(ohp13sp-sr-5の最後の3行の式を指して)この運動と向きだけ違う様な運動が、出て来ます。 で、この運動は何かと言うと、要するに、(ohp13sp-sr-5の最後の行の式を指して)z軸の方向に対しては等速運動で、z軸に垂直な方向に対しては、これはですねえ、(ohp13sp-sr-5の青色の矢印によって指示されている部分を指して)ここの符号がありますが、これがプラスかマイナスかによって、渦巻き状にz軸から(ジェスチャーを交えて)どんどんどんどんこう離れて行く様な物と、へぇから、遠くから来て(ジェスチャーを交えて)渦巻き状にz軸にどんどんどんどん近付いて行く様なものの、2種類に成ります。 で、一般には、この2つの線形結合が一般解に成るはずですので、とすると、(ジェスチャーを交えて)無限遠から来てz軸に近付いた後また無限遠に去って行く、というのが一般解だろう、という事です。 まあ、一応そういう事でねえ、で、それ以上ちょっとどう解釈したら良いのか分かりませんが、せめてもの救いはですねえ、一般には無限遠に去ってしまいますが、特殊解としては、(ジェスチャーを交えて)どんどんどんどんz軸に近付き続ける、時間が幾ら経っても(ジェスチャーを交えて)z軸から永遠に離れて飛び去ってしまわないと、そういう解も一応ある、というのが、まあ、せめてもの救いで。 そこに救いを求めなくても、別にこれで良いじゃないか、という様な理解の仕方も、あるのかもしれませんが、ちょっとそこまでは思い至っておりません。 それでですねえ、これがまあ結局結論ですね、まあ、(ohp13sp-sr-5の最後の3行の式を指して)これとか(ohp13sp-sr-5の赤枠内の式を指して)これがですね、結論という事なんですが、 「そいで」は「それで」の砕けた表現です。 「へぇから」は「それから」の方言です。 こう言ったのは、地元の広島県での発表だったからではないか、と思います。 特殊解でも束縛解があれば、この系を量子力学で扱った時に束縛状態がある、と言えそうな事に、後で気付いた。 また、元に成る方程式(ohp13sp-sr-2)は、エネルギー固有値ゼロの定常状態を決める式の形をしているので、束縛古典解の力学的エネルギーがゼロであるか否かも確認すべきだ。 ohp13sp-sr-2 チョッとポイントを言いますと、最小作用の原理という物が、こう、まあ作用が最小化される、という物がですねえ、そのメカニズムに例えられる様な物を考えてみますと、(ジェスチャーを交えて)こう作用の谷という物があって、作用がポテンシャルに成っていて、そのポテンシャルの谷にこう束縛される、という様な形で作用が最小化されるんではなくて、この場合、ポテンシャルは、作用×(-1)に成っております。 ポテンシャルは、(ohp13sp-sr-2の冒頭の式中の-(m/2)[dχ(t)/dt]2を指して)これ、作用×(-1)なんですねえ。 なので、作用はむしろ斥力、作用が最小化しない様に斥力を及ぼしてるんですね、作用はねえ。 それに対して磁場がそれを引き留めている、という形なんです。 あ、磁場に例えられる物が。 引き留めている事によって、まあ、作用が最小化される、という、そういう形に成ってるなあ、という事ですねえ。 それから、今回のは、これチョット、あれおかしいぞ、と思うのは、たぶん円環時間を使ったからだ、と思うんですが、古典解がですねえ、χ1=χ2=χ3という1個だけに、成ってます。 古典解というのは普通は無数にあるはずなんですが、何故か1個だけに成ってるので、あれおかしいぞ、と思う所があって、それがどういう事なのか分かりませんが、致命的な欠点でなければ良いんですけど。 後はですねえ、これ、nが3じゃなくて、もっと沢山の場合に、拡張できれば良いですねえ、技術的な問題に成りますが。 磁場に例えられるものは古典運動量です。 解が1個だけでいけない、と言ってしまったが、これは誤りで、ちゃんと無限個出ている。 しかし速度ゼロに固定されている分だけ解の個数が不足だ。 ohp13sp-sr-5 後ですねえ、これは、漫画できました、といって、ちょっと注意深く見れば絶対誤解するはずは無いんですが、(ohp13sp-sr-5の最後の3つの式の左辺のτを指して)ここ、たとえばこれ、時間のtを使わずにτを一応使ってるんですが、これ、普通の意味での時間じゃあないんですねえ。 普通の意味での時間というのは、(ohp13sp-sr-5の最後の3つの式の左辺の添え字1,2,3を指して)この1,2,3ですから。 一番最初に言ったか、まあ実質上言ってる事ですが、時間を1,2,3にこう離散化したわけですね、これね。 - ohp13sp-sr-4 1,2,3というのは、そもそも、(ohp13sp-sr-4を掲示して)ここですねえ。 この1,2,3というのは、(ohp13sp-sr-4の2行目の添え字1,2,3を指して)これですから、これは(ohp13sp-sr-4の2行目の時刻ε,4ε,2ε,3εを指して)ε,4ε,2ε,3εという事ですねえ。 これは何かと言うと、 - ohp13sp-sr-2 (ohp13sp-sr-2の下端の図を指して)一番最初の、この時間軸上の、この点の事ですから。 - ohp13sp-sr-5 だから、あれですねえ、時間、普通の意味での時間というのは、(ohp13sp-sr-5の最後の3つの式の左辺の添え字1,2,3を指して)この1,2,3なんですよ。 じゃあ、(ohp13sp-sr-5の最後の3つの式の左辺のτを指して)このτは何かと言うと、これは、私はまあメタ時間と呼ぶんですけれど、これは普通の意味での時間ではなくて、意味不明、まだ何の事やら良く分からない。 で、ここで考えてる、τに伴うx1,x2,x3の変化という意味での運動、というのは、これは抽象的な運動であって、普通の意味での運動じゃあないですね、ええ。 - - という事で、はい、後ですねえ、私は、高校時代は広大付属福山高校に通ってました。 広大付属福山高校の出身でですね、これは正式名称が広島大学教育学部附属福山高等学校といって、教育学部付属でですねえ、悪口を言う人は、あそこに行くとモルモットにされるぞ、という様な、そういう悪口を言う人も居たんですが、まあ私はそこで非人間的な扱いを受けた事は全くありませんが、今日なんかも、歩く教育資料がこう帰って来た、と思って頂けると良い、と思うんですけど。 そんなとこですかねえ。 はい、以上です。 「歩く教育資料」と言ったが、この高校が教育についての実験を行なう事に着目しての発言だったから、「歩く研究資料」か「歩く教育研究資料」と言うべきだった。 その意味でも、今回は、とても良い発表が出来た(第1級の研究データを提示できた)と思い、鼻高々だ。 今回の私の発表内容は、作用汎関数に対する理解を深める、という意味で、ネーターの定理に匹敵するだろう。 研究対象がそういう予後を示す事には、幾ら狙っても遭遇できないはずだ。 広大付属福山高校は、私が今まで通った教育機関の中で、このページの後半に書かれている様な問題に関して、最も潔癖だった。 この高校以外では、ある程度以上優れた事をすると意外で不条理な事に必ず負の反応が返って来たが、この高校では、言動は優れていればいるほどプラスに評価された。 特に、加藤先生の数学の機微に触れ配慮の行き届いた授業が、印象に残っている。 私は、この授業によって数学の当該期分の学力を最大限伸ばされた、という風に、今でも感じている。 その時の私の学力に丁度合っていた。 それは、今回の発表の為に必要と成った能力にも、不可欠の一角を為す形で、寄与している。 その後の学習指導要領の改変に私が批判的なのは、この授業の良い印象が残っているからでもある。 画像をクリックすると拡大します。 講演概要 27pRD-2 日本物理学会講演概要集・第68巻・第1号・第1分冊・13ページより。 OHP OHP-sr-1 OHP-sr-2 OHP-sr-3 OHP-sr-4 OHP-sr-5 2013年03月27日撮影分＠学会発表の実況＠動画 質疑応答時間には、鈴木貞吉さんと私の間で、以下の様な問答が行われた。 発言者 発言内容 注釈 鈴木 その文法なんですけどもね、そこのエックス1乗、2乗、3乗は、例えば矢野先生のリーマン幾何学の参考書を見ると、x軸、y軸、z軸だと。 いわゆるテンソルなわけですよね。 矢野健太郎著「リーマン幾何学入門」森北出版の事だろうか？ 宇田 テンソル？ - 鈴木 うん。 だから、僕の場合は、テンソルと、まあ解析とですね代数との間にある矛盾て言うか、それが、1が0に等しいという、そういう矛盾を持ってると、まあ、そういう事を、まあ、説いたわけですよね。 だから、文法という、そういう概念の中に、そういった、まあ、テンソルを微分でもって、テンソルというのは微分でもって完全に表す事が出来るんだ、という事をね、文法にしたいのか、まあ、そういう所が良く分からないんですよね。 何が文法を言ってるのかね。 まあ何度も私、まあ質問して申し訳ないんですけれども、そこん所の意味合いって言うかね、それを是非説明してもらいたい、こう思うんですけどね。 - 宇田 ちょっと仰る意味が良く分からないんですが、でもまあ推測で言うと、テンソルを微分で表せるという事が言いたいのか、という質問が含まれてますよねえ、鈴木さんの今の、何かそう仰った。 それは、私は多分、だから、テンソルを微分で表せるという事が私は多分言いたいんじゃないだろう、多分違うだろう、と思います。 それから、まあ、細かい事ですが、あれ、エックス1乗、2乗、3乗じゃなくて、あれ、エックス1、エックス2、エックス3で、冪の1,2,3じゃないです、あれは。 「仰る意味が良く分からない」という言い方は、相手の意見を否定する時には、私にとって使いたくない表現です。 何故なら、しらばくれる際に用いられる事が多いからだ。 相手の言ってる事の意味が良く分からないが、その意味を推測して、その推測に基づいて答える、という不自然に積極的な態度を私が取ったのは、そのためだ。 物理学正典 > 初等力学正典 > TEC-0-1-7の補足説明欄に、8行目についての補足説明として、添え字の説明が書かれています。 鈴木 うん。 だから、それだとね、矢野先生は、だから、エックスの1乗はx軸なんだと、こういう風に書かれてるわけですよ。 テンソル解析って言うか、あれの中にね。 だから、まあ結局、使ってるのは微分だ、と思うんですよね。 微分を使って、こう、やってると思うんですよね。 スカラー場の導関数がベクトル場(1階テンソル場)に成る、とか、ベクトル場の微分が2階テンソル場に成る、という知識に基づく発言だろうか？ 宇田 ちょっと分かりません、意味が。 鈴木さんの質問が上記の意味だとすると、私の発表内容は、そういう事を主張する物では、全くありません。 鈴木 だから、そこん所がねえ、何を狙ってるのかね、良く分からない。 文法というね、文法というからには、何かそういう一般概念的なね、ものを目指してる、という意味がある、と思うんですよね。 - 宇田 そうですねえ、はい。 - 鈴木 その意味が良く分からない。 - 宇田 ああ、そうですか、う～ん。 これは今まで何回にも渡って少しずつお話して来た事なので、今回のだけ、という事に成ると、ちょっと、その前提抜きだと、分かり難い面がある、と思います。 今回のは、私の言ってる文法とは何か、という話じゃないので、もっとその文法の話を特別なこういう場合について適用してみると、という様な話に成っておりますので、今回の話からその文法というのは、ちょっと、文法一般というのは何か、というのは、ちょっと分かり難いでしょうねえ。 今まで何回にも渡って少しずつして来た説明を、いずれの回にも、鈴木さんは、出席して聞いていた。 鈴木 だから、時間が、こう、リング状にね、循環するというのは、それは当たり前なわけですよね。 - 宇田 いや、そんな事ない、と思います。 循環する時間は、私以前に既出だが、当たり前ではない。 宇宙論にそういう宇宙モデルがあったかな、と思うが、宇宙は当然そう成っているだろう、とは考えられていない。 また、私の発表は、いずれの回においても、円環時間というアイデア自体の独自性を主張するものではない。 日本物理学会2009年秋季大会での私の発表の独自性は、文法物理学の問題への円環時間の活用であって、円環時間自体ではない。 鈴木 例えば、時間を質量でもって表す事が出来る、とかね。 - 宇田 いや、それも聞いた事ないですねえ。 時間を質量で表す事は出来ないだろう、と思う。 ohp13sp-sr-4のM=mεα2が、鈴木さんには時間を質量で表す式に見えたのだろうか、と想像するが、この式は、そういう式ではない。 座長 あ、すみません、時間超過しておりますので。 で、今日午後のセッションはこれで終わりたいと思います。 どうも有難う御座いました。 - 以上。 理学研究科棟で発表した事で、分かる人が聞いていたなら良いなあ、そして今後の他人の研究動向に影響が出れば良いなあ、と思った。 自分の発表を終えた後で、BA会場の「ダイバーシティー(多様性)と物理」セッションに途中から参加した。 参加してみて、私が日頃から特に心頭に発するまで怒っている問題がテーマらしい、と分かり、ここで是非ひとこと言っておかねば、と考えて発言した。 この問題については、普段の生活では、自分の意見の中のその場で腹が立った事に該当する部分、が思い出され、しかし、自分の意見の全体を一度に思い出す事は無かった、そういう自分の意見の全体が、今回は一度に頭の中に出て来た感がある。 私のこの意見は、感覚としては、かなり子供の頃から一貫して揺るぎ無く全体的にまとまっていたが、言葉にはまとまっていなかった。 言葉にまとめるのは困難だったからだ。 そして、機会の平等の成立を隠然と妨害する者は、その様な説明の困難性を良い事に詭弁を弄し、もつれた糸を目の前に放り投げて、解けるものなら解いてみろ、解けるまではそれが糸である事は認めん、といった態度に似た、間違ってると言うんだったらどこが間違ってるか言ってみろ、というシラバックレた態度の一点張りで通し、発語障害者の感じるであろう苦しみを、被害者に味わわせ続けて来た。 道理で、下記の私の見解の全体を即時会話でスラスラと答える事は今までは不可能だったろうし、この見解の局部をアッチを取ったりコッチを取ったりして逃げ回れば、それ自体としては正しいんだが、と評価される事だけを言いながら、批判者につかみ所を与えず、ずるずると何時までも批判から免れ続ける事が出来ただろう。 私自身、書き出してみるまでは、こんなに込み入っている、とは思わなかった。 会場では私は「この問題には詳しくない」と断った上で発言したが、「このセッションには詳しくない」と言うべきだった。 私以外の人々による議論には私の目に見て指摘すべき点がたくさんあった、という事は、結局この問題について私は詳しかった様だ。 何と、この問題は、私が渦中の人である所の問題だったのだ。 当日帰路携帯電話から自分のPCにメール送信したメモを、とりあえず以下に掲載し、その後で、それを加筆・修正した。 とにかく一刻も早く皆さんにお見せしたかった、からだ。 後で書き足して行くと、書くべき事が際限無く思い出し足されて収拾が付かなく成ったので、これでは大意の読み取れない文章に成ってしまう、と思い、途中からは推敲のみとし、書き残した事は相対正義論や宇田経済学のページに書く事にした。 ダイヴァーシティのセッションに参加して、発言した。 発言しなかった部分まで含めて、機会の平等と結果の平等の対立の問題について、私の見解をまとめる。 生来固有の属性は性別だけではない。 ---↓勘違いだった↓--- 異なる属性間の該当人数の相関関係が、ある属性を基準にして結果の平等が成立していれば別のある属性を基準にすれば必ず結果が不平等に成る事、を保証する。 そう成らないのは、相関が全く無い場合だけだ。 しかし、実際には相関は有るだろう。 よって結果の平等は、それ自体が不可能である。 ---↑勘違いだった↑--- 各属性の全体における含有比率がどの部分集団においても再現されている様にする事は、組み合わせとしては可能らしい、と気付いた。 例えば、血液型については、A型の人数が全人口の10%, B型の人数が全人口の20%, O型の人数が全人口の30%, AB型の人数が全人口の40%だとし、性別については、男の人数が全人口の51%, 女の人数が全人口の49%だとすると、大抵の職位や大抵の学籍の各々について、それに所属している人数の10%が血液型A型で、20%が血液型B型で、30%が血液型O型で、40%が血液型AB型で、51%が男性で、49%が女性だ、という風に成っていなければいけない、血液型と性別以外のあらゆる生来固有の属性についても、そう成っていなくてはいけない、という平等観念は、内部矛盾を含まない。 これは結構魅力的な考え方だと思う。 これを、先天形質均等ブレンド方式と呼ぶ事にする。 結果の不平等は機会の不平等の存在の証拠とは成らない。 この理由としては、フェアな競争の結果が生来固有の属性の各々について均等に分布する事は保証されない、という事だけでも十分である。 フェアな競争の結果が生来固有の属性の各々について均等に分布する事なんて(論理的な不可能事ではないが実際には確率的に非常に起り難いだろうという意味で)有るわけない、と思う。 しかし、結果の不平等は、その実態が、機会の不平等の存在を強く示唆している場合がある。 結果の不平等のこの様な特徴を根拠にアファーマティブアクションを行なう事、には私は肯定的である。 しかし、これは、機会の平等が成り立っていた場合に生じたであろう結果を手動で復元しようとするものであり、大いに誤り得る(不正の温床に成る)ので、全面的に賛成、ではない。 機会の平等が正しく、結果の平等はそれと両立し得ないので間違っている、というのが、私の持論だ。 もっと正確に言うと、私の意見は、公正な競争の結果がたまたま平等に成っている事を、結果の平等だからいけない、と言って批判する意見ではない。 私が批判するのは、結果の如何(格差等)を理由にしての、結果の事後的な取り消しや、結果が平等に成る様に競争の条件を調節(特に事後的に変更)する行為だ。 「結果の如何を理由にしての」というのは、ルールの欠陥やルール違反を理由にしてのではない、という意味だ。 私は、競争の公正さの観点からなら、結果の事後的な取り消しや、競争の条件を調節(事後的な変更も)する行為を、如何なる場合でも例外なく不当だ、とは考えない。 私は、絶対的貧困等の絶対的に不幸過ぎる結果については、‘結果の事後的な取り消し’や‘結果を理由にしての競争条件の調節’に反対する自分の持論に固執しないが、現行の社会保障の考え方でこの問題が完全に解けている、とも思わない。 社会保障は、それが存在しない場合の統計に対しては妥当でも、それが存在するという知識に基づいて人々が行動する場合の統計は、それとは異なるからだ。 機会の平等が成り立っていてもなお生じる結果の不平等については、これを平滑化しようとするアファーマティブアクションには、私は強く反対する。 それは、もうこのぐらいでいいじゃないか、などという贅沢な理由によってではなく、機会の平等に反するからだ。 その種のアファーマティブアクションが機会の平等に反する、というのは、それがフェアに競争したら勝ったであろう人から結果を奪う、という事であり、これは競争の機会を奪う事に等しい、という意味だ。 ゴリ押しで「この人を入れろ」と要求する事は、他の誰かに「お前、降りろ」と要求する事と表裏一体だ。 実力の首位者が地位の首位に就かない様に、という配慮が感じられる。 弱きを助け強きを挫く、という標語の真の意味は、ここにあるのかも知れない。 それは、言葉だけではなく密かに守り行われている可能性がある。 強い者が勝つのではいけない、という標語の真の意味もこれか？ 女生徒に将来像を見せるために女性教授が居るべき、という発表者の見解は、女性がその職種に向いているという考えの根拠、に分類されると思う。 また、教育の内容の事まで言うならば、女生徒に与えられる‘教育を受ける機会’が男生徒に与えられる‘教育を受ける機会’に等しく成る様にそうすべき、という考えだと考える事も出来る。 したがって、この意見は、機会の平等が成り立っている場合の結果の手動復元を超えての結果への介入を主張するものとは直ちには言えないが、もっと突っ込んで考えると、そういう内容を含んでいる気配を感じたので、会場で私は確認しようとした。 この問題は、非線形系の時間発展の見地から考える事も出来よう。 女性教授が居なければ女生徒が女性教授を目指さない、女生徒が女性教授を目指さなければ女性教授は居なくなる、というポジティブフィードバックの問題としてだ。 この問題意識は、会場で発表者によって述べられるのを聞くまで、私は知らなかった。 この事は、貧富の格差については、格差が再生産される、という言葉でよく耳にする。 非線形系は初期条件の偏りを何時までも記憶するので、長時間経過後の偏りにも有意性は無い、という言い方が出来よう。 これは、自由市場競争が最適値を自動的に算出するだろう、という楽観的な予想への有効な批判だと思う。 しかし、機会の平等に対しては妥当する批判だが、適材適所を論駁するには至らない。 なぜなら、この批判は、機会の平等は適材適所や結果の平等を達成する手段として不完全である、という指摘であって、適材適所の欠点や結果の平等の必要性を指摘するものではないからだ。 私が大学生だった頃は、実力主義という言葉が、適材適所と同じ意味で、肯定されるべき価値を表すために、良く使われていた。 近年、この実力主義という言葉が聞かれなく成った事にも、私は不審を感じる。 会場では、アファーマティブアクションは多様性実現の手段だとされ、適材適所実現の手段だとされるのは聞かなかった。 だから、これは良からぬ事である気配が濃厚だ。 機会の平等の保障は、適材適所達成の実際的な手段であるが、達成率100%の適材適所を保証するものではない。 と言うのは、機会の平等に基づく公正な競争は確率過程であって、これによっても、適材が100%決定論的に適所に配されるわけではないからだ。 また、先述した非線形系の時間発展の性質も、機会の平等が適材適所を保証しない事の理由と成る。 機会の平等への侵害は、女は男に勝つな、とか、年下の男は年上の男に勝つな、という不正な圧力によって隠然と存在する。 隠然とである事と‘勝つな’という要求内容は、勝った者はそれ相応に処遇しなければいけないという競争原理と機会の平等を侵害者自身が肯定している事、の証である。 この不正な圧力とは、女なのに男に勝ったり、年下なのに年上の男に勝ったりしたら、その勝った人に対して、悪い事をした犯罪者である、との倒錯した闇の判決が下り、その凶悪残忍な実態を不当にも歪めて嫌がらせなる穏やかな言葉で世間では言い表されている手法によって、暴力の結果と同等の結果を必ずや生じさせる事のみを最終目的とする攻撃が、生意気にも処罰の名目で発動され、この最も暴力しか信じない暴力主義者の手先が、暴力はいけません、と唱えながら押し寄せて来る、という行動版屁理屈、それ自体が慈悲や猶予を一切含まない処罰の対象と成って然るべき犯罪行為と、それへの依頼・協力の事であり、この不正な圧力は、俺は偉いんだ→偉いから俺には勝つな→誰も俺に勝てなかったから俺は偉いんだ、という循環論法に属する詭弁の、実証を頑なに拒む無限ループ、を回そうとする者達によって運営されている。 それは、あたかも、私は嘘つきではない、したがってこれは嘘ではない、故に私は嘘つきではない、と言うかの如くだ。 他人を評価しない口実として、実験物理学は健全で理論物理学は不健全だ、という偏見を盾に取る人に、その様な‘実証を頑なに拒む人’が多い事は皮肉だ。 現代においては、物理学の根幹を進歩させるイニシアチブを取ろうと本気で考える時には、理論的手法に頼る方が見込みがあり、実験的手法に頼ってもほとんど見込みが無い、という見通しに対して、顧みるに足る反論は存在しないはずだ。 上記の偏見は、この事に対するシラバックレであり、実は、それ自体を取っても、不誠実の証拠と見なせすらする。 劣った学者が、自分の無能ぶりやライバルの有能ぶりを素人の目から隠す、のに使う詐術の類だ。 ただし私は、女の方が男より上等だと言っているのでも、年下の男の方が年上の男より上等だと言っているのでもない。 年上の男に見られる年下の男に対する曲がった態度という物は、学生時代に私が、自分と同じ学年の学生の私に対する態度の中に見た、フライパンの焦げ付きの様にシツコイ曲がった態度と、本質的には同じだ。 この事から、年上の男の年下の男に対する、自分は先輩だから、お前は後輩だから、という言い分は単なる口実であって、その実は、もとから曲がっていた者が成長できずに曲がったまま年長に至っているに過ぎない、というのが真相だ、と分かる。 また、女の采配の下でその采配の曲がっているのを実感した事、もある。 女性は常に、セクシャルハラスメントのセクシャルの部分を他のありとあらゆる概念に取り換えて、自分を律するべきである。 セクシャルな物だけ言うのはフェアではない。 性別年齢にかかわらず、曲がっている事は有りがちな事であり、曲がっていない事は希である。 大人は子供を馬鹿にするが大人はやり方が巧妙に成っているだけでやってる事は小学生と同じだ、という意味の事を私は、非難と軽蔑の意味を込めて言った事がある。 独り言でだけだったかもしれないが、言ったのは確かだ。 全ての大人が、というわけでもないし、小学生の中にも性質の善い人も居るので、その点については、語弊がある発言だったと思うが、大筋においては今でもその通りだと思っている。 それは、こちらが嫌だなあ、と思う事に誘っておいて、こっちが勝ちそうに成ると、誘った本人が、もうやめようよ、と言い出したり、こっちの勝ちで終わる事をこっちの勝ち逃げだズルいと言い掛かって罵り始める様な小学生のズルい態度である。 この態度は、結果の平等主義者の態度と質的に良く似ている。 人生経験として、1つの種目で(スゴロクに例えて)上がりそうに成ると他の種目を勧められる事が多い、と私は実感している。 暴力主義と正義の違いは、暴力を禁止するか許可するかの違いではない。 正義では暴力を最後の(＝最も避けるべき)手段と考えるのに対して、暴力主義では最初の(＝必ず用いる)手段と考える、それだけだ。 正義も暴力を完全否定はしない。 暴力主義者は、間に非暴力攻撃を挿入して相手に暴力を振るわせ、それを口実に暴力を振るうが、暴力はどんなに遠回しに行使しても暴力である。 暴力主義者は、言葉にも暴力は有る、として、言葉で為された事に対して暴力で報復するが、そんなのは言い訳であって、本当は、暴力の方が言葉よりも痛いから暴力を用いる、言葉での攻撃では満足できないから暴力を用いる、甘えた奴に過ぎない。 これは、暴力主義者が、言葉は暴力に満たない事、を知っている証拠だ。 不正な圧力については、それじゃあこれから改めます、という態度すら私は、もう許すつもりは無い。 私が特に怒っているのは、不正な圧力を行使する者が逆に私に対して怒っている事、に対してだ。 怒る、というのは、正しい者が間違った者に対して取る態度だ。 間違った者が正しい者に対して怒る事は、生理的に不可能であり、‘怒った振り’であり、それは‘笑って誤魔化す’ならぬ‘怒って誤魔化す’である。 あくまで怒る者の主観での正しいか間違いかだから、しらばっくれる余地はあるが、先述した様に、不正の隠然性が、それはシラバクレに過ぎない事、を証している。 本人が正しいと思ってるんだったら表沙汰にするはずだ、からだ。 また、私が受けようとしている評価を、他の人が受ける事に対しては批判しないが、私が受ける事に対しては批判する、宇田雄一だからいけない、という考え方が感じられる時にも腹が立つ。 これは、宇田雄一は勝つな、という形態での、機会の平等への侵害と見なされる。 つまり、女性差別や人種差別ならぬ宇田雄一差別である。 この様な個人差別の甚だしく間違っている様子は、漫画「ドラえもん」で、「のび太のくせに生意気だぞ」というジャイアンの台詞によって浮き彫りにされ、からかわれている。 ----↓枝葉末節↓---- 物理学会での発表においても、私が発表している、という事自体に対して筋違いな恨みを持っている、易きに従って老い難きに阻まれて学は成らなかった(老害もまた言い訳)が塩漬けにしておいた自分の学問株を取り出してみれば思いの外上がっている事に味を占めた鈍くて自惚れの強い生意気な年上の男先生、が例外的にではなく居る事を、何年にも渡る観察を通して私はハッキリと確認している。 ある回には、座長が火が付いた様に食って掛かって来た。 あれは、ハッキリと不当な脅迫だ。 また別のある回には、慣性力についての私の発表内容を間違いだと誤解した人の表情に、その事がありありと表れていた。 間違ってるだけなら怒るはずがない。 ある回には「誰にでも発表する権利はあるんだけど」と言いながら、発表するな、という事をほのめかして来た老先生も居る。 私の発表内容の貧しさを口実にしていたが、その人の発表内容を見て、それはやはり口実に過ぎない、と分かった。 また、ある時期以降は、何故か、そういう類の人と同じ会場に同席する事が無く成った。 この事にも、私は、負の配慮を、感じている。 ある回には、空き時間に会場で、年上のある男性参加者と対話している途中に、私が相手の話を聞いた上で、いざ自分が話そうという瞬間に、老年の男性参加者が、それを妨げる目的で、話に割って入って来た。 それでも、結果的には私は何とか妨害をかわして自分の意見を言ったが、妨害された事、妨害をかわすのに必要な能力が私以外の人には普通は備わっていないだろうレベルに達していた事、その分、その能力の発揮に必要な精神集中と、妨害をかわす行為の成功の不確かさが、大きく、ストレスを感じさせられた。 この老年男性は、その後、別の空き時間に、私をポスターセッション会場に誘って、その道すがら、自分は応用物理学会に所属していて、そこでは、入会してから最初の20年間は発表しない風習がまかり通っている、という事を、肯定的とも否定的とも取れない口調で私に語った。 若造は発表するな、ポスターセッションにしておけ、という事を私に遠回しに言ったのだな、と今では思っている。 肯定的とも否定的とも取れない口調であったのは、一つには、発表するなと要求はしてないと主張するためのアリバイ作り、である事が考えられ、もう一つには、私に是非をコメントさせないための工夫だったのではないか、と考えられる。 肯定的か否定的か、どちらかの口調で言うと、私が「それは無いんじゃないですか」とか「とんでもない事ですねえ」という風にコメントする可能性がある。 これを言わせない事によって、私が黙認した、という風に事態を曲解しようと狙われた可能性がある。 私は、もともとは、ある論文をJPSJに投稿して、それが却下された際に、送り返されて来た封筒に入っていた文書に、学会で発表なら出来ます、と書かれていたのがキッカケで、学会発表をする様に成った者だから、発表を自粛しろ、という態度(要求されてすればもはや自粛ではないが)が感じられた時には、無性に腹が立つ。 また別のある回には、ある有名な先生がエレベーターで私をセクハラ罠に掛けようと狙っている、のに気付き、階段で降りた事もあった。 降りると空襲警報の様なサイレンが鳴り出したが、それはまるで私が罠に掛からなかった事に対してである様だった。 不愉快極まりない。 セクハラ罠は少なくともセクハラと同程度の処罰を受けるべき犯罪であるから、早くそうして欲しい。 インターネット掲示板でも、私について意見交換が行われている最中に、学会で発表したという事実は発表した人の能力について何らの証明にも成らない、という意味のメッセージが投稿されて来る事が、良くありました。 これは、事情をよく知らない人が、宇田雄一は学会で発表したのでこの人の学力は折り紙付きだ、という風に誤解するのを防ぐためのもの、と思われ、内容的には間違っていません。 これなんかも、私が何か目立つ事をして騒ぎに成ると、「ああ、なんでもない、なんでもない、なんでもないんですってば。こいつは、なんでもないやつなんです、ほんと」という風に揉み消しに来るものとして、私の目には映っています。 新装開店の店の前でライバル店の回し者が、これはなんでもないんです、って言ったら、これはもう立派な営業妨害である。 近年、公道を通行中に、私に対して、自動車、自転車、歩行者、あらゆる形態で、危険運転、迷惑運転、交通事故を引き起こそうとする行為が、ものすごい多頻度で仕掛けられて来ますが、これも、上記と無関係ではない気がします。 物理学関係では、私のウェブサイト物理学正典が談合の壁を突破して既存の権威の相対的評価を低下させている事との関係性を最も疑っていますが。 また、この事は、ネット上での私への攻撃がそれらのネット版であった事、を物語っています。 物理学正典は、既存権威が出した物理学解説サイト、よりも、ユーザーの信頼を勝ち得つつある、という風に私の目には映っています。 既存権威がタッグを組んで腕にヨリをかけSEO的にも翼賛体制が敷かれているあのサイト、を見ても、案の定、轍風だった。 やっぱりな、であった。 それは、当然そうだろう、と思う。 私は、それを悪い事だ、とは全く思わない。 そういうコンテンツの存在を理由にして、お前は余計な事をするな、と言ってさえいなければ、逆に、余計な事をするな、と言われる筋合いが無いのも同様である。 私がした、という事は、宇田がしなくても他の人ので足りる、という批判の不当性が私には正覚裡に判明した、という事である。 私がした、というのは、そういう事である。 唯一アイツだけが非権威系だが、アイツの正体は談合系ガチンコだろう、と私は睨んでいるし、内容でも大差を付けているつもりだ。 この他に、Googleに対する法的な手法での攻撃や、2ちゃんねる閉鎖話も、私は、私の競争力を低下させる目的で行われている可能性がある、という風に睨んでいます。 Googleの機能を低下させる事は、t****erやF****ookにユーザーを囲い込む事と対を為す、と私は考えています。 2ちゃんねる閉鎖は、証拠隠滅を狙ったものだ、と思っています。 ユーザーを囲い込む方は失敗に終わるでしょうけど。 ユーザーを囲い込む、というのは、インターネットの中に小領域を作り、その外には普通は誰も出ないものだ、という文化を醸成する事で、セキュリティ上の脅威の増加も、これに一役買っている。 Googleの機能を低下させ、談合会員が運営するサービスにユーザーを囲い込むと、何が出来るか？ 非談合会員の成功をコントロールできる。 非談合会員が、談合会員が運営するサービスの枠内で自分のコンテンツを構築すると、まず、スタートを出遅らせる事が出来る。 まずは、そこで一旦、そこまでの非談合員の富の蓄積をリセットする。 出遅れても挽回した場合には、誠に勝手ながら、と言って、サービスを終了すればよい。 言い訳の為にデータ継承ツールを提供しても、コンテンツの価値をかなり減ずる事が出来る。 そうやって、非談合会員の勝手な富の蓄積をリセットする事が出来てしまう。 私は、この観点から、クラウドについても警戒が必要だ、と思っている。 手元にバックアップを残して、自分のクラウドが閉鎖されても、コピペ程度の手間で他のクラウドに乗り換えたり、オフライン作業に切り替えたり出来るのでなければ、かなり怪しいと思う。 旧来の談合勢力は、囲い込み以前の問題として、そもそもインターネット自体を不都合だと感じている様だ。 その事は、インターネット上での出来事を「ヴァーチャル」という言葉で表す所に表れている。 電話での会話を「ヴァーチャル会話」と言うだろうか？ 言わない。 電話でしようが、対面してしようが、会話は会話だ。 同様に、ウェブページに書こうが、紙出版をしようが、著作は著作だ。 それをヴァーチャルと言うのは、インターネットを駆使して作られた事実を事実として認めたくない、という見苦しい逃避だ。 タイヤに縞々状に泥が付いた状態で自動車が走行した場合に出るザッザッザッ・・・という断続的な音で、現実の出来事ではない、という事をある映画が表現しようとしている、と感じた時にも、その表現を、私に関する事実に対する同種の逃避だ、と思った。 私の自宅の前を、同じ内容を表意する目的で、この音を出しながら自動車で走った者も居る。 この走行音については、読者には伝わらないだろう、とは思うが。 もっと言うと、インターネットの爆発的普及による紙書籍からウェブサイトへの土俵の切り替えという物が、そもそも、私が紙書籍「古典物理学」を完成させた事への、ガンディーの発言機会に彼を多数者の中の一人の状態にして彼の発言を目立たなくしたとされるイギリスのやり方と同様の、対処だろう、と私は見ている。 土俵を紙書籍からウェブサイトへ切り替えると同時に談合系ガチンコを1人立て、私の出遅れを無駄にしない、という事まで行なわれている。 これだけの不利な条件を私は今では全て跳ね返して見せた。 すると今度は、実空間での暴力がやって来た。 これは、犯人が尻尾を出した、という物だ。 ----↑枝葉末節↑---- 会場で私は、年齢は生来固有の性質ではないので年齢による差別という概念は存立し得ない事を、18才未満飲酒喫煙禁止という規則を差別とは言わない事を指摘する事によって、説明した。 この他にも、20才未満には選挙権が与えられない事や、25才未満には被選挙権が与えられない事も、指摘できよう。 年齢は生来固有の属性ではないので、年齢を理由にした権利の制限というものは一般には間違っていないが、勝つな、と要求する事は、間違っている。 勝った場合にも何歳に成るまではコレコレのポストは待ってくれ、という要求なら、正しい場合もある。 勝つな、とは言えないものだから、尊敬しろ、と言う。 言えない言わないという事が、‘勝つな’と要求する事は不当である事を‘尊敬しろ’と言っている者自身が自覚している、事の証拠である。 恐喝者が、金を出せ、とは言えないものだから、誠意を見せろ、と言うのと同じである。 ----↓枝葉末節↓---- 天才とは、生まれながらにして本質に於いては長老よりも長じている事、である。 その事情は、ある分野の初心者が、その分野の読み終わったばかりの本(人生という名の書物)について、それをまだ読んでいないその分野の第一人者に、読んだ上で意見を聞かせろ、と言って指導を仰ぐ際に、まだ読んでいない第一人者の方がもう読み終わった初心者よりもその本の内容について本質においては長じている事、に例えられる。 いくら第一人者でも読む前から分かるはずがない事と、初心者が読んでも分からない事、の両方がある。 ----↑枝葉末節↑---- 勝つ、という意志決定は存在しない。 出来るだけ勝つ様に努める、という意志決定なら有る。 従って、勝つな、負けろ、という要求は、勝たない様に努めろ、という要求だと理解するしか無い。 勝たない様に努める、という事についても、深く考えるならば、そうしようがすまいが事実のレベルでは勝敗は変わらない。 と言うのは、手加減して格好上負けた事は本当の意味での負けではなく、手加減させて格好上勝った事の方が本当の意味では負けだからだ。 したがって、そういう意味では、勝たない様に努める、という事も本当は不可能である。 従って、勝つな、負けろ、という要求は、格好上勝たない様に努めろ、格好上負ける様に努めろ、という意味に解するしかない。 しかし、この要求は本質的には演劇において劣役に強要される事であり、この様な強要が許容されるのは、特定の劇団の様な不参加が任意の小さな集団の演劇活動に限定される話であり、その様な小集団でも団員の私生活にまでは妥当しないし、不参加の任意性が小さい職場においては、さらにその分だけ、そういう強要の許容性は、小さく成る。 ましてや、生来終身常時参加不可避の母集団のルールとしては、そういう強要が許容される余地は皆無である。 社会の大前提にその様な強要が存在する事は、人権の平等に対する直接的な否定に他ならないからだ。 年齢は生来固有の性質ではないが、年齢が違っても人権は同じでなくてはいけない。 血液型がB型である若者に対して、長老といえども「いや、お前はA型だ」という認定を押し着せる事は、人権の否定の域に達しているので論外である。 自分がどういう人であるかの事実について、そうではない、という認定を押し着せる権利が他の誰かにある、と考える事は、異なる個人の人権の間に差を設ける事であり、これは人権の平等に反する。 人権の平等に反する考え、とは、分かり易く言うと、私は人だがお前は人ではない、という驕った考えである。 こう言えば、年齢や社会的地位もこの道理を歪める正当な理由には成らない事、が良く分かろう。 年齢や社会的地位に基づく処遇は、基部としての人権に基づく平等な扱いにオプションの如く付け足される形でのみ、許容・奨励されるものであり、人権に基づく平等な扱いを侵食する形で許容・奨励されるものではない。 どういう人であるかの事実には、能力はどれだけか、知識はどれだけか、善良さはどれだけか、という事も含まれる。 相手の事実を否定や歪曲しない事は、相手を尊敬する事よりも基本的な道義、相手を尊敬する事の第一歩であるから、相手の事実を否定しておきながら‘俺を尊敬しろ’と要求する態度は、倒錯した不当な態度であり、逆に、自分の事実を否定する相手に対して敬意を欠く態度を取る事は全く正当である。 優秀さの表出を、内容が優秀であるから、という理由で制限する事が不当な事は、また、他人の面目によって自由を制限する事はあまりに自由を制限し過ぎて不当だ、という風に根拠付ける事も出来よう。 つまり、そういう制限は、ほとんど自由という概念全体の否定であり、それでは一体何なら自由なのか、という批判を免れない。 他の誰かよりも勝(まさ)っている、という理由は、行為を制限する理由としては優先順位が最下位の理由であり、自由主義とは、これを正当理由として認めない正義感だ、と私は理解している。 勝負の指し示す範囲が、将棋やテニスの様に、特定の相手との対戦であるなら、その人とは勝負するな、という要求は限定的だが、単独行為に自然に付随する評判についての競争なら、勝負するな、という要求は、指し示す範囲が広く成り過ぎて、何も自由に出来なくなってしまう。 後者についての‘勝負するな’という要求は、誰も俺より賢い事を言うな、とか、誰も俺よりカッコいい事をするな、という、ほとんど未熟者のカンシャクにおいてしか見られない様な、する事が恥である様な、要求を誰かがする、という事であるから、その事によって要求した人の名誉が守られる、という事は有り得ない。 将棋に例えると、人権は歩(ふ)であり、オプションの如く付け足された権利は飛車(ひしゃ)や角(かく)である。 将棋でも、実力に著しい差があれば、飛車角落とし(ハンディキャップの一種で最初から自分の飛車と角を盤外に外しておく事)て勝つ、という離れ業が可能であるのと同様に、実社会のルールも、極めて順当にも、そう成っている。 これは、権力の濫用に対して権力無しで勝てる様に成っている、という意味ではない。 濫用をルールは肯定しないからだ。 上司がこなすべき仕事を部下がこなす、という事でもない。 上司の上司としての業績よりも部下の部下としての業績の方が顕著である状況、などを思い浮かべると良いのではないか。 上司の劣った采配を部下の服従の優秀さがカバーしている状況とか。 あるいは、演劇で主役と脇役の実力差が大き過ぎて主役の状態がほとんど顔ハメ記念撮影だった、という状況とか。 これは実際に起こり得る事で、松本清張原作の「点と線」という有り難～い推理小説の映画版の一つで、映画監督として名を為した演劇以外の分野の出身のある高名なタレントさんの演じた主役の状態が、顔ハメ記念撮影だった、と私は思っている。 勝つな、という要求の不当性に話を戻すと、こちらが勝負しない様に努めていても、相手が勝負を仕掛けて来る事がある。 将棋やテニスなら、断る事も出来よう。 (ちなみに、私は、将棋もテニスも弱いので、自分の方が勝つから断る、という事は無い。) しかし、こちらの意志とは無関係に、相手の意志だけで勝手に始まってしまう勝負もある。 これは正当防衛の論理に成るだろうけど、そういう場合についてまで、勝つな、とは要求できないはずだ。 例えば、自分が勝負のつもりは無く既に言ってしまった事に対して、誰かから「それは間違っている」と言われたらどうするか？ 間違っていなければ、間違っていない事を証明するのは当然の権利だ。 しかし、それをすると、相手が負けてしまう。 この負けは、相手の身から出た錆であり、相手の自業自得である。 もう一つ例を挙げれば、ある人が自分の事を馬鹿だ馬鹿だと言いふらしている事に気付いたので、みんなに良く見える様に賢い事をして見せたら、それを見たみんなに、な～んだ賢いじゃん、という事が分かってしまい、自分の事を馬鹿だ馬鹿だと言いふらした人の信用は失墜して、今度はその人が笑い者に成る、というケースが考えられる。 これも、言いふらした人の、身から出た錆であり、自業自得である。 このケースの場合には、その人を打ち負かした行為は、単に許容されるだけでなく、賞賛される様な事である。 そういう場合に勝たない様にする事は、優しさの問題としてはあるかもしれないが、優しさは義務以上の事だから優しさなのである。 従って、勝ったという事を呵責する態度という物は、優しくない事よりも、もっと呵責されるべき事である。 他者に全く介入する事なく自分の身の振り方だけで優劣に関する濡れ衣を晴らす、という、この飛車角落として勝つ見本の如き態度についてまで、傷付き易いからそうするんだ、というケチを付ける者が居るが、それは傷付き易さの相場に対する吹っ掛けである。 それを傷付き易いと言うんだったら、それじゃあ、誰も俺より賢い事を言うな、とか、誰も俺よりカッコいい事をするな、という要求を発するカンシャク野郎は、一体何なんだ？ 傷付かな難い、か？ 正確には、傷付く、というのとは感情の種類が違う。 自分の身の振り方だけで優劣に関する濡れ衣を晴らす、という態度の動機は、それに対するカンシャクの動機から筋違いな成分を除去して得られる感情を何分の1にか希釈した様な感情である。 また、もっと深く考えると、諸事実の無矛盾の連鎖というものは、その波及範囲も関係の強さも不測であるので、自分の意見は正しいのに、目の前の相手が可哀そうだからといって、それを曲げたら、別の何処の誰がどんな不利益を被るか分からない。 この意味で、そういうのは、真の優しさではない、と言える。 それは、遠くの誰かから奪い取った物を目の前の人に与えて、私はこんなに良い人です、という風に表現する類の偽善である。 目の前の人に優しくすると自分の居心地が良く成り、遠くの人に嘘をついても自分の居心地は悪く成らないので、それは本質的には、優しさではなく利己主義である。 そして、近接2者間の配慮(面と向かっての言い難さ)を利用して言葉を曲げさせる事によって第3者を侵略してやろう、という目論見は実際に存在している様に感じられる。 第3者への配慮という観点は、物理学などの学問上の真理についての論争においては、その必要性がハッキリしていて分かり易く、その分だけ負けたくない気持ちが強く成るが、負けただけなら恥で済むが、曲げると非難の対象に成るので、他人に挑戦する場合には、負けた場合に軟着陸できるような挑戦の仕方をするのが、身の程を知っている、という事だ。 無謀な挑戦の仕方をしても、大恥に耐える覚悟があるなら、相手に失礼という事を除いては、それでも良いが、耐えられなく成って曲げる方に逃げたら、それはもう、自分のした選択の結果に責任を持てていない、という事である。 これは、学問の場合には、学者の責任感という物に含まれるだろう。 この場合の自分のした選択とは例えば、「あなたの言う事にちょっと分からない部分があるんですけど」と問いかけるか「あなたの言ってる事は間違っている」という風に断定するか、の選択であり、大きく勝つために後者を選択した、という事です。 負けた場合に軟着陸できるような挑戦の仕方とは、前者の事です。 もちろん、実際に相手の言う事が間違っていたなら、断定で構わず、その分大きく勝てますが、相手の言う事が間違っていなかったら、断定した分だけ自分が大きく負け(どの面提げて、といった状況に成り)ます。 間違った非難とも成ると、単なる間違った断定よりも、もっと悪い。 つまり、これは賭博と同じであって、大きく賭ければ、勝ったら大きいけれど負けても大きい。 小さく賭ければ、勝っても小さいけれど、負けても小さくて済むわけです。 小さく賭けて軟着陸というのは、具体的に言うと、刑事コロンボがやっている様に、「いやあ、実によく分かりました、さすがですねえ、恐れ入った、あはははは」で済ませる、という事です。 逆に、常に勝ち続けるならば死ぬまで終始一貫して不遜な態度で通す傲岸街道一直線、というのも十分に‘有り’です。 この態度への賛美は、「荒野の七人」という西部劇映画の中でユル・ブリンナーに対してホルスト・ブッフホルツが福音史家的に述べる賛辞に、見る事が出来る。 (この映画の基に成ったとされる日本の時代劇映画「七人の侍」に、同様の表現が含まれているかどうかは、知らない) つまり、傲岸街道一直線は、‘有り’どころか、誰もが、出来るものならそう在りたい、と考える模範、理想であり、小さく賭けて軟着陸するやり方は、そう出来ないから仕方なくする次善策に過ぎない。 因みに私は両者の折衷様式です。 該当する負けが無い人を不遜だからという理由で攻撃する事は、ルール違反に該当し、不遜である事よりももっと悪い事です。 何も間違えず何も謝らない人は悪で、何か間違えてそれを謝る人は善だ、なんて、そんな本末転倒な正義は無い。 間違えないに越した事は無いが、間違えて謝るのでも構わないよ、と考えるのが正しい順序だ。 そうでなければ、そもそも、間違いが間違いではない、ではないか。 自分には出来ないからといって、出来ない方が良いんだ、と考えるに留めるなら、それも慰めの論理として許されようが、だから出来てした人を罰するのだ、という所まで来ると、負け惜しみも大概にしろ、との非難を免れない。 これは、公正な自由競争全てに通じる事で、結果の平等が如何に正義に反するか、を良く表しています。 間違い、というものは、出来るだけ間違えない様にして下さい、という風に暗黙裡に要請されている事項であるので、出来るだけ間違えない様に努力するのは当然の事である。 この時点で、まず、間違えない様に努力した事を非難する事は不当だ、という事が言える。 その様に努力しても全く間違えないのは困難だが、もし結果的に全く間違えなかったならば、間違えなかったので謝る必要は全く無い、のも当然である。 謝罪は間違いや間違えない様にする努力を怠った事に対しての物だからだ。 何も間違えず何も謝らない人は悪だ、とする事は、少しぐらいは間違えろ、と要請したり、間違えなくても謝れ、と要請する事と等価である。 間違えなくても謝れ、と要求する態度は単純理不尽であるし、少しぐらいは間違える様にしたら、その結果生じた間違いを捉えられて、謝れ、と言われるに決まっている。 間違えろ、と言われて間違えた事に対して謝罪を要求されるのも理不尽であるので、これで、何も間違えず何も謝らない人は悪だ、とする態度は理不尽な態度である、という事が、言えた事に成る。 要請が暗黙である分だけ、それを自主的に汲んで行動すれば、その要請が存在しない事を前提とした批判を自分が受ける危険があり、その事から身を守るために、ますます、間違えない様に努力する権利があるのも、当然である。 出来るだけ間違える様にして下さい、とか、少しぐらいは間違えるようにして下さい、という風に要請されたならば、その要請に応えた間違いという物は、(要請した者に対する)間違いではない。 上記の「間違いが間違いではない」とは、こういう意味です。 それを「間違い」と言うとしても、その間違いは、要請した者に謝る類の物ではないので、その間違いもそれを謝らない事も、悪ではない。 要請した人以外の人に迷惑が掛かる様な間違いという物については、間違え、と要請されても、それに応じる事は、出来ない相談である。 つまり、何も間違えず何も謝らない事を悪だとする主張は、誰かが自分に勝った、という事実を、その人が自分に悪い事をした、という風に捻じ曲げようとする道具に過ぎず、無効である。 御覧の様に、どこをどう曲げても、正を誤にしたり、誤を正にしたりは出来ない。 正からは正が、誤からは誤が、導き出されるのみである。 この様に自分の意志とは無関係に始まってしまう勝負については、勝たない様に努力する義務は有り得ないし、勝たない様に努力してはいけない場合もある。 従って、勝つな、という要求は、従う事が不可能であり、不可能であるから不当である。 まず最初に、勝負する権利があるからそれは不当であり、百歩譲っても従う事が不可能だから不当である。 本人以外には、本人にとって有利な事実を否定する権利は、無い。 裁判が良い例だ。 自慢は、格好悪いだけで、悪ではない。 天才が、それ以下だと認識されている状況は、犯罪を犯していない者が犯罪を犯した者として認識されている状況と同様である。 後者を非難版(善悪版)の濡れ衣と呼ぶならば、前者は侮辱版(優劣版)の濡れ衣だと言える。 非難版の濡れ衣を着せられた者が、自分の身の潔白を証明する際に、それが証明される事によって他の誰かの面目が潰れる事をかえりみる必要は、全く無い。 (この観点については、19日＠2012年07月＠日記にも、書かれています。) して見せなければ(それが自分には出来るんだという事を)信じてもらえない様な事を出来る能力を持つ者が、して見せる事によって自分の能力を証明する際に、それが証明される事によって他の誰かの面目が潰れる事をかえりみる必要が微塵も無い事は、これと同様である。 モーツァルトが悪でサリエリが善、という表現は見た事が無い。 そういう表現が無いのは、モーツァルトが悪でサリエリが善、という認識が間違っているからだ。 念のために言っておくが、これからそういうもの(モーツァルトが悪でサリエリが善、という認識を表現する映画)を作っても、言い訳でしかないぞ。 あれ程までの屈辱を味わわされてもサリエリにはモーツァルトに何かを止めさせる権利は全く無い、それが正義である。 そして、私を含めて多くの人は、そういう正義観に好感を持ち、サリエリに対してはザマアミロぐらいにしか思わない、それが人の健康な感じ方である。 犯罪の才能を犯罪の実行によって証明する事は、してはいけない事だが、これとて、犯罪だからいけないのであって、それが証明される事によって誰かの面目が潰れるからいけない、のではない。 事実の否定に立脚した正義、というものは存在しない。 事実と真実は異なる、という事情も、これを覆すものではない。 ここまで、隠然とした不正な圧力の不当性について、詳しく述べて来ました。 この不正な圧力は、アファーマティヴアクションを肯定する向きにも働いているし、否定する向きにも働いています。 競争の不公正を是正するアファーマティヴアクションに対しては、不正な圧力は、それを否定する向きに働いているし、表面的な結果の平等をゴリ押しするアファーマティブアクションに対しては、不正な圧力は、それを肯定する向きに働いています。 ----↓枝葉末節↓---- 私の成し遂げた事(文法物理学の樹立)は、やって見せるまでは信じてもらえない様な事であり、して見せる前にそれがどんな内容かを説明する事、すら出来なかった物だ。 知ってる人に対しては「ご覧の通り」と言いたい。 (予見的には説明できなかったために、「自分探し」とか言う何かわけの分からない事を私がしている、という濡れ衣を着せられていた気配を感じるが、私は、20才頃以降は、常にマッシグラであって、自分探しなんてした事は一度も無い。) 私の能力は、そういう事が出来る能力であり、私の才能は、そういう能力に達し得る可能性だ。 20才頃には私は、自分がソレダケノモンである事、を確認し終わっていたので、そういう生き方は、私にとって権利と義務の両方である様に、感じられた。 才能は生まれつきのものである。 自分の才能を私は子供の頃から自他の対照観察によって薄々知っており、大学卒業時点ではハッキリと自覚していた。 子供の頃は「自分は天才だ」という自覚によって生じる考えを公言し、大学卒業後はそれを無責任な放言として反省して、黙ってやってみせる方針に変えた。 しかし、黙って結果だけを出していると、いつまでも惚け(しらばくれ)続けられる事が分かった。 その結果、また言う様に成ったので、実際に黙っていた期間は短い。 言う様に成ったのは、自分に対する態度を改めさせるためではない。 しらばくれる手段として、私に直接接する人は、私の能力の、世界談合協同組合の天井を突き破って屋根の上に出ている部分、を見てもそうと分らない人だけに成る様に、人選されている。 それだけでも不正であるのに、その上に、私の天才性のあまりの明白さ故に、鈍く人選された人の目にもそれが分かってしまった時ですら、全身疾患の自分達の私に触れた部分だけが治癒した、という事実から目を背け、自分たちはほとんど健康だが私に触れた部分だけが病変した、という風に白を切って自己欺瞞を貫き、その人を病変部分として切り捨て、私の言説をまるでウィルスか何かの様に勝手に位置付け、私の周りをマスクをしてうろつく。 私の母校である大学の先生Kは、勤務地が東京から山口県に変わった。 これは、上記文脈における病変部分として切り捨てる事に当たる左遷だろう、と私は思っている。 この人は、私の言説に納得しているわけではないと思うが、火が付いた様に座長Sが食って掛かって来た件について、その座長の態度の不当性を説明するために、Sが批判したのと同じ事をK先生は肯定的に評価した、という事を私が学会発表＠活動報告＠学問＠宇田英才教室内に書いたからだ、と思う。 この事件の背景をもう少し説明すると、座長Sが火が付いた様に食って掛かって来たのは、表向きは私の発表の事務手続き上の不備(そんな不備は存在しなかった)や会場での表現形式の不親切さ(みなさんに分かる様に、というのがルールであるのに分かり難かったのでルール違反だ、という難癖)であったが、本当の理由は、私の発表がSの権威を根拠付けている親権威への攻撃と見なされたからだ。 私にとっては、そういう発表をしない限りは、どんなに優れた事を発表しても、独学者にしては、という評価しか得られない、という観点からも、そういう発表をする事に意味がある。 私の場合、どんなに偉い学者の書いた物の中にでも、単なる誤植よりは大きい、学術上の、に属する間違いを見付ける事が、希にではあるが、当然そういう事もあるよ、という形で、ある。 それは、私が偉い事を意味するだけであって、その学者が偉くない事を意味しない、ので安心しろ。 どんなに優秀な人が作ったコンピューターソフトにも事後的なアップデートが止め処なく続く事が常識として知れ渡っている今では、その事が理解されよう。 自分は天才で大きな事をするから待ってろ、みたいな事を言わなくなってから、私がその考えの間違いに気付いて恥ずかしくて言えなくなった、とか、夢を捨てた、という風に解釈した者も居るであろうが、それは誤解である。 (私がそう言わなく成ったのは、オーディオ機器販売で客から「この安い方の製品でも音質は十分ですよね？」等と訊かれた店員が後で騙して買わされたと言われない様にする為に「それはお客様に聴いてもらって自分の耳で判断して頂く事に成っております」という態度を取る、のと同じ理由でだ。) 故意の曲解の場合すらある、と思っている。 広島県福山市神辺町の現住所で1990年代後半に、近所から法螺貝を吹く音が「ブオワ～、ブオワ～」という風にしばしば聞こえて来ていた時期があった。 2000年を過ぎてからは当分聞かなかったが、2013年現在を基準にしてここ数年の間に、また何度か聞いた。 私に対して、お前は法螺ふき(大嘘吐き)だ、という風に表現する嫌がらせの可能性がある。 私は、20才の頃から2013年(45才)の現在まで、理論物理学で顕著な業績を打ち立てる、という目標を、人生の第一志望から外した事は、一度も無い。 心に迷いが生じた瞬間はあるが、それは、悩み事のレベルに留まる物であり、行動のレベルでは一貫して目標を変えた事は無い。 ----↑枝葉末節↑---- 林檎取りで背の低い人に補助具を持たせるのは、林檎の個数が人数を超えている場合には、問題無い。 しかし、そういう状況を思い浮かべてしまう分だけ、この論法は詭弁である。 実際の社会問題は、林檎の個数が人数よりも少ない奪い合いの状況に対応しており、この状況では、背の低い人に補助具を持たせても、勝者が背の高い人からスバシッコさ等の無形の能力に優れた者に変わるだけで、やはり誰かが負ける。 誰しも、自分の能力のうちで他者よりも優れている種類の能力で競う権利があるはずなのに、それを奪われるのは不当である。 外見を見て分かる優秀性の行使は不当なもので無形の優秀性の行使は正当なものだ、という考えは、能力種への差別である。 能力差の効果を相殺するルールや設備を幾ら導入しても、それは、競争をますます不可視な能力での競争に変容させるだけであり、そうやっても、やはり強い者が勝つのである。 したがって、強い者が勝つのではいけないからそうした、という主張も、屁理屈である。 アメリカの銃倫理に、銃は等化器だ、という思想があるそうだ。 これは、銃を用いなければ生存競争における有利・不利が体格という先天的で固有の要素に支配されてしまうので、そういう差をキャンセルする銃の様な等化器を用いる事が正義にかなう、という思想だ。 しかしながら、等化器を用いると、強者が体格の良い者から早撃ちの得意な人に変わるだけで、やはり、強い者が勝つ。 その様子は、漫画「ドラえもん」において、銃ありの場合にはのび太がジャイアンでありジャイアンがのび太である、という状況として描かれている。 西部劇では、早撃ちの得意な実質上の最強者がたまたま正義の味方である様に成っているが、それでは、体格の最も良い人がたまたま正義の味方であるのと何ら変わらない。 たまたま、では、いけないのだ。 これは、等化器の思想の抱える最も本質的な問題点であろう。 ----↓枝葉末節↓---- 擦り足で極度にソロソロ歩くアレが、衝突されたという言い掛かりを免れるための対策だとしたら、それが優勝者の仕草の象徴である事は、その種目が、最も無意味な、無意味どころか負意味な競争(他者に言い掛かりを付けて陥れる競争)である事を表しているだけであり、それもまた強いものが勝つ、である。 そういう奴が、もっと有意味な種目での競争を、それでは強い者が勝つからいけない、として批判するのは、詭弁だ。 有意味な競争の優勝者を自分の宴会に呼んで、どんなに長じても自分以下だ、という事実が成り立っているかの様に演出するやり方も、陰湿である。 ----↑枝葉末節↑---- 強い者が勝つのではいけないから、といって、多数の弱い者が結託して強い者1人をやっつけた場合も、やはり強い者が勝っている。 それは、多数の弱い者が力を合わせれば強い者1人よりも強い、という自明の理を表しているに過ぎない。 そして、それに対して、強い者1人が負けたから善い、という評価を与える事も、間違いである。 善いか悪いかは、強いか弱いかとは別だからだ。 強かろうが弱かろうが、正しい者が勝つ事が善いのだ。 弱くて間違った者が勝つ事も、強くて間違った者が勝つ事と同様に、災いである。 強くて正しい者が勝つ事も、弱くて正しい者が勝つ事と同様に、幸いである。 ここまでに説明した様に、勝つのは常に強い者であり、もし弱い者が勝ったなら、その弱い者の方が実は強かった、というだけの事である。 強い者が勝つのではなく勝った者が強いのだ、とは、この事である。 したがって、肝心なのは、弱い者をいかにして勝たせるか、ではなく、正しさと強さを如何にして一致させるか、である。 つまり、正しければ強い、間違っていれば弱い、という力の法則を、如何にして人間社会全体に通用させるか、という問題である。 (もっと言うと、正しい者に、勝つという作業、を課す事すら不当であり、正しい行ないは全く抵抗を受けないのが理想である) 補助具の導入というものは、強弱差を相殺する、という観点からではなく、そういう観点で見なければいけない。 その意味では、インターネットという補助具は、正しければ強い、という法則の通用を促進している、と思う。 私が子供の頃には、ほとんど何にも恵まれていない人が、でも自分はこれでなら勝負できる、というものを偶然持っていて、それで立身出世する、という、なんて可哀そうなんだ、から、超すげー、に至るまでのサクセス・ストーリーが、自由主義陣営の自己正当化の子守歌として、しばしば聞こえて来た。 確かに、そんなのは例外中の例外(そんな武器を持っている人は希少)で、そうでない大多数の人には何の救いも与えないかもしれないが、その事も、その例外中の例外である人から、自分にはこれしか無いんだ、という生活手段を奪う正当な理由には成らない。 私は生まれつき皮膚に葉緑体があって光合成出来るので稼ぐ必要が無い、という人が居ても、他の人には真似できないから光合成を禁止します、とは言えないだろう、という事だ。 林檎が獲れなくても、それじゃあミカンにしてください、って成るだけなのに、まるで食いっ逸れるかの様な印象を与える所も、林檎取りの補助具の寓話は、詭弁である。 背の低い人が、たとえ自分がミカンに向いていてもミカンじゃあ嫌なんだ、という風に駄々をこねている事を隠蔽する作用も、林檎取りの補助具の寓話は、詭弁的である。 さて、林檎取りの補助具の寓話が会場で出たのは、職位獲得競争で負ける人にアファーマティブアクションによって与えられた職位を、背の低い人に与えられた林檎取り用補助具に、例えての事だ、と私は理解している。 そういうアファーマティヴアクションが妥当な場合、というのは、自力では就けない職位をアファーマティヴアクションによって与えられた人が、その職位の仕事をこなすに足るだけの能力を持っている、という事だから、これは、職位獲得競争のルールに問題がある場合だ、と言えないか？ いや、自分が仕事をこなせても、自分よりももっと上手くこなせる人がたくさん居れば、自分はその仕事には就けない、というのは、間違いではないから、必ずしもそうは言えない。 しかし、そうだとすると、そういうアファーマティヴアクションの正当性というものは、需要を満たす必要性によって理由付けられるものではなく、就職したい人の(幸福追求・自己実現の)権利の観点から理由付けられている事に成る。 そこで、アファーマディブアクションを、次の2つの種類に分類する。 第1種 向いてる人が優先的に採用される、という職位獲得競争のルールを肯定した上で、それが守られていない、という理由で、守られた場合の競争結果を手動で復元しようとするアファーマティブアクション。 第2種 需要を満たす必要性の観点からだけでは、向いてる人が優先的に採用されるという職位獲得競争のルール、に必然性が無い、という理由で、そのルールを否定し踏み倒すアファーマティブアクション。 林檎取りの補助具の寓話が会場で出た事から、アファーマティブアクションとしては、普通は第2種の物が考えられているのではないか、という風に私は推測する。 第1種のアファーマティブアクションについては、競争を経ずして競争結果が分かるものか(反語表現)、という難点がある。 第2種のアファーマティブアクションについては、その是非は、就職したい人の(幸福追求・自己実現の)権利の観点から既存の職位獲得競争のルールに必然性が有るか否かに、掛かっている。 もし有れば、第2種のアファーマティブアクションは、却下されるべき物である。 また、需要を満たす必要性の観点からだけでは本当に、向いてる人が優先的に採用されるという職位獲得競争のルールには必然性が無いのか、という点についても、検証が必要である。 第2種のアファーマティブアクションの動機に成っている「必要性が無い」とは、向いてる人が優先的に採用されるのでなくても供給の不足は生じないはずだ、という考えです。 つまり、適材適所にすれば出力が最大に(同一出力に対しては苦労が小さく同一苦労に対しては出力が大きく)成るけれど、別に出力を最大にしなくたって世の中ちゃんと回るじゃないか、それより、あまり向いてない人にもその仕事をやらせてやれよ、という考えです。 もっと原理にまで遡ると、生産では専ら報酬のみを目的とし、幸福の追求は消費で行なう、という経済の原則に根がある。 つまり、報酬以外の点で自分の仕事に不満がある人は、転職するよりは今の仕事の報酬で贅沢でもしなさい、という考え方です。 あるいは、就職時には報酬のみに着目して最も多くの報酬を得る事が出来る仕事を第一志望とするのが幸福追求の定石であり、報酬を犠牲にして生産満足の高い仕事を選んでも、そうして高めた生産満足なんて、犠牲にした報酬で買える幸福に比べれば、取るに足りない些事だ、という考え方です。 経済が請け負う幸福は、必要な物、欲しい物が買える状態であり、生産する喜びの様な物は経済の副産物に過ぎない。 働かざる者は食うべからず、という諺にも現れている様に、経済においては、生産する事は、あくまで消費するために払う犠牲・負担であり、その量や強度が小さい事にではなく、それ自体に幸福を感じる、という幸福感や価値観は、経済という物のターゲットには成っていない。 経済においては、出来るだけ生産の苦労と所要時間を減じ、出来るだけ消費の量と質を高める事が、進歩であり、生産に限って言うなら、苦労も所要時間もゼロ、という状態が上限であり、それ以上つまり生産する喜びの様な物は、それを超えた話である。 つまり、手柄を立てる喜び、とか、困難な生産を成し遂げたという名誉というものは、経済が人に与えようと目指しているものではない。 その様な手柄や名誉を求める心というものは、経済の基準では、マゾやフェチ以外の何者でもない。 私は、この様な経済の価値観に全面的に賛成だ、と言っているのではなく、この様に経済という物には生身の人間の心に完全にはフィットしないガサツな所があるのでそれが問題の根に成っている、という話をしています。 第2種のアファーマティブアクションは、消費のみを幸福の尺度とする経済の価値観の至らなさ、に呼応するものだ、と考えられよう。 なぜ、この原理が関係しているかと言えば、最も自分に向いているが報酬の正当性以外の点で不満な仕事から、その不満を解消するために自分の適性に逆らって別の仕事に転職し、ミスマッチの分だけ報酬が減る、という状況と、元の仕事に留まったまま報酬の一部で娯楽を購入して不満を解消する場合とを比較する時、転職に伴う報酬の減分と娯楽購入代金の大小関係が、社会全体における適材適所の達成率によって左右される、からだ。 (1)適材適所の達成率が低ければ、娯楽購入代金の方が大きく成り、転職の方がお得です、という計算に成る。 (2)適材適所の達成率が高ければ、転職に伴う報酬の減分の方が大きく、娯楽購入の方がお得です、という計算に成る。 どちらに転ぶかの(適材適所の達成率の)境目の値を求める事が、需要を満たすためには適材適所の達成(出力の最大化)が必要である、という主張に対する検証と見なせる。 なぜなら、(1)が成立している場合には、適材適所の達成率を下げる向きの転職が動機付けられ、その結果適材適所の達成率が下がり、適材適所の達成率が下がると、ますます、適材適所の達成率を下げる向きの転職が強く動機付けられる様に成り、その繰り返しで、際限無く適材適所の達成率が下がる負のスパイラルに入り、適材適所ハザード(分業破壊)が起きる、のに対して、(2)が成立している場合にはその逆である、という事が言えるからだ。 (1)の状態というのは、誇張すると、「んあ？買うに値する素晴らしい物なんて、そんな物ねーよ」という状態、「金持ちに成りたいですか？」と訊かれて反語的に「成ってどうするんだ？」と答える人が多い状態であり、経済やお金という物が人気を失ってシラケた状態だと言えます。 これは各人が職業選択を自由に行なう場合の話であって、(1)ではシステムダウンを防ぐために自由を制限する、という事にでも成れば、(1)と(2)の違いは自由であるかないかの違いに直結する。 (2)では、納得づくの契約のみの積み重ねによって全体の秩序が維持され、どこにも強制は存在しない、いわゆる神の見えざる手だ。 (1)で自由が制限されれば、損な選択を強いられた事に対する納得できない気持ちが社会全体に蓄積される。 取引に対する納得や満足は、当事者の本音で測られねばならない事だ。 本音という物は、直接には表面に出ない。 アンケートの結果も究極的な当てには成らない。 口論で勢い余って吐かれた暴言も、攻撃技としての威力を増そうとするあまり、本音で思っている以上に相手を悪く言う傾向があるので、本音とは限らない。 これは、小学生が口喧嘩で「おまえのかーちゃん、でーべーそ」と節を付けて歌う時に本当にデベソだと思っているわけではない、のと同じである。 恋愛ドラマの主人公が自分の本心に少しずつ気付いて行く過程の描写にある様に、本音は、究極的には、本人にも分からない面がある。 だから、みんなが本音では何を望んでいるのかは、まず仮定して、それに基づいた制度を置き、その運用結果から間接的に推定するしかない。 これは、言葉は本音と食い違い得るが取引態度は本音と正確に一致する、という意味ではない。 言葉でも取引態度でも完全にやせ我慢を貫いた場合、取引をする各人の活力が低下し、それがマクロ経済の指標に不健全の印として必ず現れるはずだ、と私は予想する。 それに加えて何より、やせ我慢で何処にもボロが出ない経済が回ったとしても、それでは、いったい経済は何のためにあるのか、という事に成る。 我慢を減じ満足を増加させるのが、経済の目的であるはずだ。 ---↓枝葉末節↓--- アファーマティブアクションが消費者に痩せ我慢を強いているのではないか。 売る時には買い手に奉仕し、買う時には売り手に奉仕する、という事では経済は沈滞してしまう。 テレビが、見れて良かったね、の時代が終わって、出れて良かったね、の時代に突入している、気がする。 テレビが面白くなく成って来ている、という人が居るが、その原因ではないか。 こうでなくてはいけないと言うがそんなの別にこれでも構わないでしょ、という批判と、それに基づく基準緩和が、十年とか二十年前に有ったのではないか、と私は疑う。 そして、そういう変化が有ったとして、その批判が間違いである事は直ぐにはハッキリとは分からなかったが、十年ぐらい見ていると結構ハッキリと分かって来た、という目で私は見ている。 テレビ番組のコンテンツの中で東京的な物の人気獲得競争力が圧倒的に強いとされていたジャンルに、大阪的な物がゴリ押し入って来たとか、そういう事が有るんじゃないのか、という風に私は感じる。 ---↑枝葉末節↑--- 分業というものが経済に合理性を与える理由には2種類がある、と思う。 一つは、各人が分担する種目が自給自足の場合に比べて少なく成る事によって合理性が生じる、という事であり、もう一つは、各人の仕事内容に占める得意分野の割合が自給自足の場合に比べて増える事によって合理性が生じる、という事だ。 適材適所ハザードは後者の崩壊を意味し、前者の崩壊を意味しないから、分業破壊と言っても、直接的には、部分的な破壊に留まる。 残った半分の合理性だけで経済を運転する方式、というのは、最初の方で述べた、先天形質均等ブレンド方式に、対応するだろう。 この様な問題意識を分かり易くするために、私は、転職のパラドクスという物を考え出した。 自動車会社Aで働いている人αが、自分は今の仕事に最も向いているのだが、自動車会社Bの仕事にもっと大きな魅力を感じる、しかし、自分は自動車会社Bの仕事には非常に向いているわけではないので、AからBに転職すると、明らかに給料は下がる、現在の給料でならB社製の高級乗用車が買えるが、Bに転職するとそれは不可能に成る、それでも良いんだ、と言ってαはBに転職した。 こういう状況を考える時、αの価値観では、B社製の自動車を生産する事には価値があるが、B社製の自動車にはあまり価値が無い、という矛盾した内容が同時に含まれている事に成る。 面白く言うと、俺が一番欲しいのは(消費するための)カネだ、という態度を取らない事は、アインシュタインの「ずーっと前方には自分の後頭部が見える」的な意味で、自分の仕事の商品価値の否定と同義である、という寸法だ。 これは、実は、高尚な学問を志す、という在り方に対しても、ケチの付け所として、妥当性を保っている、と私は思っている。 工業製品を通してにせよ文物を通してにせよ、学問は、買える物を通して貢献する分野の域を出ない。 したがって、買える物の消費より学究を、という態度は自己矛盾である。 因みに私は、自分は学問に最も向いている、と思っているので、自分は学問で稼ぐのが一番儲かるはずだ、と信じている。 この認識は後で、アテ価値とツモリ価値についての考察において、修正を受けました。 正確には、自分の生産の結果が社会にとって有意であるから生産満足を感じる、というのではなくて、生産行為の触感に満足を感じる、という有り方も論理的な可能性としては、ある。 しかし、それは少数派だ、と思う。 学問で言うと、物を考えるのが好きだ、とかいう感じ方は、それだが、あなたが考えている事は全部既に何かの本に書かれているよ、という状況であるかないかで、考える喜びに雲泥の違いが出る事は、学問を志した事のある人なら、誰でも知っている事だろう。 考えるという自分の行為が人類を代表しての物に成っている(自分が人類の脳細胞として機能している)と感じる瞬間にのみそれは雲レベルの喜びであり、既に何かの本に書かれている事を考えている、と感じる場合には、それは泥レベルの喜びにしか成らない。 生産行為の触感に満足を感じる、という在り方は、緩衝材のプチプチを指でつまんで潰すのが気持ち良くてやめられない、みたいなもので、それは泥レベルの喜びであり、フェチズムに該当するだろう。 経済は欲望を原動力として作動する、と言われるが、欲望は全て経済の運行に寄与するかと言えば、そうではなく、欲望の中にはそれとは逆向きの欲望もある、というのが、論点です。 経済の運行に寄与する欲望というのは、消費したいという欲望であり、それとは逆向きの欲望というのは、生産したいという欲望です。 前者を正の欲望と呼び、後者を負の欲望と呼ぶ事にします。 経済の価値観では、正の欲望は利己心、負の欲望は利他心、と成るのでしょうけれど、アファーマティブアクションに見られる様に生産も奪い合う物だ、というのが実情である事を踏まえると、負の欲望も、利他心と言うよりは欲望と呼ばれるべき物でしょう。 短期的には、正の欲望は経済の出力を上げる向きに、負の欲望は経済の出力を下げる向きに、作用する、という言い方が正しいでしょうか。 自分の本音での生産欲を大雑把にチェックするリトマス試験紙として、私は、次の質問を考え出した。 「もし働かなくても買いたいものは何でも買えるだけのお金を持っていたとしても、その仕事をしますか？」 答えが「はい」ならば、その仕事に対する生産欲がある、答えが「いいえ」ならば、その仕事に対する生産欲は無い、と判断できる。 この質問を自問してみると、仕事が人から生産欲を持たれる事が如何に難しいか、が分かろう。 他人に質問したら、大抵の業種については否定的な答が返って来るだろう。 それと同時に、生産欲を持たれる様な極少数の例外的な業種という物が、くっきりと浮かび上がって来るはずだ。 負の欲望は確かにある。 プロボクサーにとって戦果への欲求が報酬への欲求を凌駕する事は明白だ。 また、人物Aを買い手とする売り手Bが、Aには出来ない事をいとも楽々と上手にこなす、という状況を考えてみても分かる。 経済学的には、Aは、その事を、丁度良かった、という風に考えるはずだ。 しかし実際の人間は、丁度良かった、と思うと同時に、シャクに障る、という感じ方もするのが普通だ。 これは、遠くは、Aも分野を限定しない広い意味では売り手としてBと競争しなければいけないので脅威を感じる、という事が背景にあるからなのかもしれないが、AがBの脅威から安全であっても、そういう感じ方をする。 人間の心は、そういう風に出来ている。 脅威だから、というのは、何故そういう風に出来ているかの進化論的な理由であって、それは、なぜ負の欲望はあるのか、と問う事に等しい。 昭和の時代には、プロは、客に、私はこの仕事にこんなに向いています、あなたには絶対に無理でしょう、というアピールをしていた物です。 経済学的には、その方が客は得するので喜ぶからです。(テレビで言うと、見れて良かったね、の感覚) テレビの前の良い子は絶対に真似するな、というのは、客を喜ばせる為ではなく、用心の為に発せられた言葉だが、そういう背景と良く調和する。 それが、最近では、プロが客に対して、自分の仕事の難しさを謙遜し出した。 いえ、いえ、こんなのは大した仕事じゃないんですよ、あなたでも、やれば直ぐ出来ますよ、という風に。 これは経済学的には変な話です。 客にも出来るんなら、わざわざカネを出してやってもらう必要はない、という風に成るからです。 しかし、経済学とはズレているけど、これもまた、人の心の性質に沿っている面があります。 職場への新入りが何も教えられなくても既に必要な事は全て出来る能力を持っている事を、できあがっちゃってる、という言葉で表現して目の敵にする光景をテレビで頻繁に見た時期が有った。 これも、上記の「シャクに障る」の具体例だろう。 会社にとって、被雇用者が最初からデキアガッチャッテル事は経済学的には、丁度良かったじゃないか、と言われるべき事だから、先輩職員がそれに対して負の対策を講じる事は、会社への背任ではないのか。 負の欲望の他の例としては、人生における夢という概念が挙げられよう。 子供に「夢は何ですか？」と尋ねると、どの生産を分担する人に成りたいか、という意味で「・・・に成りたい」という風に答えるのが普通だ。 どういう消費をしたいかを夢として答える子供、も居るかもしれないが、それは、パーセンテージとしては少ない。 大人から質問されて子供が答える夢が生産欲の充足である事は、子供の遠慮や背伸びかもしれない。 遠慮というのは、消費欲の充足を答えると‘図々しい’とか‘厚かましい’と思われるのではないか、という考えだ。 私には、子供時代に、他の子供が生産欲を答えるのを傍聴して、そう思いながら、自分は正直に言おうとして消費欲を答えた、という事が有った様な気がする。 私自身は、欲望としては、子供の頃は消費欲が支配的で、大人に成るに従って徐々に生産欲が台頭して来た気がする。 欲望と聞いて「しめしめ、欲望があるという事は需要があるという事だ、供給すれば儲ける事が出来るぞ」と考えるのは、負の欲望に関しては、早合点だ。 なぜなら、生産欲というのは名誉欲であり、その充足は供給に伴うものだからだ。 名誉という物は、供給を受ければ受けた分だけ減る類のものである。 名誉をカネで買おうとする行為が不名誉の典型である事、は周知の事実である。 従って、俺にカネを払ってくれればお前の名誉欲を充足させてやる、という形式の商売は存立し得ない。 経済に関わって生産の欲望を満たす、というのは、本人の自由だが、これは、言ってみれば裏ワザの様なものであって、例えて言うなら、車体の振動で全身にアンマを掛けるために自動車に乗る、みたいな事です。 そして、職種によって生産する喜びが異なる、という事情は、自動車運転のアンマ効果には個人差がある、という状況に例えられるでしょう。 自動車が、誰が乗っても移動するという本来の用途に関しては効果に差が無い様に責任を持って作られている様に、経済も、消費幸福を得るという本来の用途に関しては万人に公平です。 生産幸福が職種で異なる、というクレームを経済に付ける事は、アンマ効果に個人差がある、というクレームを自動車に付ける事に、例えられ、間違っています。 それと自分の価値観との食い違いは、経済の改造にではなく、経済との距離の取り方に反映させるべきである。 経済という物を擬人化すると、次の様に成る。 消費欲望の不満を抱えている人の所に、経済という人がやって来て、次の様に言った。 『生産への相応の協力をしてくれれば、あなたが欲している消費財を与えます。 と言っても、私はやり方を教えるだけですが。 どういう選択をするかは、あくまであなたの自由なんですが、私としては、あなたに、消費欲望の充足を最優先にする選択を期待しています。 具体的に言うと、生産種目の選択においては、内容ではなく報酬で選んでほしい、という事です。 それは、実情を見たあなたがしたい様にした結果がそう成っている事を期待する、という意味であって、要請ではありません。 そう成るかどうかは、私の腕前次第であり、そう成らなかったら、それは偏に私の力不足によるものです。 内容がどうであれ報酬の高い仕事に就きたいとあなたに思われる状況を作る事は私の方でやっておきます。』 そう言って経済は立ち去ったが、やっておきます、の内容が知りたくて後をつけてみると、おおよそ、他のたくさんの人にも同じ事を言っているだけだった。 それを見て、経済の言った「私の腕前」とは、人の心に占める生産欲と消費欲の比率を見抜く能力の事だったのだ、と私は悟った。 したい様にした結果がそう成る状況という物は、頑張れば出来そうな感じがする出来るかもしれないと感じる生産結果に伴う生産欲の充足値を、頑張れば買えそうな感じがする買えるかもしれないと感じる消費財による消費欲の充足値が、超えている、という状況であり、これは、十分に魅力的な消費財が十分な個数市場に出回っており、生産競争が激しく生産でチャンピオンに成るのは難しい、という状況、つまり、経済全体の出力が十分に高まっている状況に他なりません。 これは、一人も例外者が居ない様に成り立っていなければいけない事ではなく、大勢において成り立っていればよい事であり、全ての人がしたい様にしている限りにおいては、例外の人と例外でない人が互いに他をタダ乗り者呼ばわりするのは間違いです。 例外者は経済の期待に反する選択をする人ですが、もしこの人に消費欲の充足を優先させる事を強制したならば、したい様にしている人々がしたい様にし続けるためになぜ私がしたくない事を我慢して行なわなければいけないのか、という極めてもっともな反論(経済に参加したくない人を強制的に経済に参加させている事から来る要求限度の存在の指摘)を受ける事に成るでしょう。 この様に、放逸さの観点からは、したい様にする、の内容は完全に無制限だが、相場を操作する事を目的とする取引が禁止されねばならない等、犯罪の観点からは、無制限ではない。 また、これは、正確には、必要条件に過ぎず、さらに、欲しい消費財を買おうとすると避ける事が出来なく成りそうな成るかもしれない種目の生産に伴う負担の嫌さと、欲しい消費財への消費欲を、天秤に掛けた時に、消費欲の方が勝っている、という条件も必要です。 一言で言うと、したくない種類の生産も嫌過ぎではない、という条件です。 これは、生産による与益ではなく生産に伴う負担に着目した条件で、経済というものは与益のみに着目し負担の事は考えないので、経済の盲点と言えるかもしれない。 一般化すると、受益に対する欲望である所の生産欲と消費欲の他に、負担に対する忌避感情も、欲望のリストに付け加える必要がある、という事です。 生産欲と消費欲は「したい欲」と呼び、負担に対する忌避感情は「したくない欲」と呼ぶ事にします。 経済が人の心に完全にはフィットしていない、というのは、極めて微妙な話であって、かなり良くフィットしてはいる。 どのぐらい微妙かと言うと、大抵は手柄の大きな仕事には大きな報酬が伴うので、経済と人の心のズレは、それらの微弱な食い違いだけだ。 手柄の大きさと報酬の大きさが少ししかズレないので、生産者が報酬目当てで生産しているのか手柄目当てで生産しているのかは、外見上は分からないのが普通だ。 また、何かの分野でチャンピオンに成る、みたいな場合を除いては、生産よりも消費の方が嬉しい、というのが真実である。 その事は、「何だかんだ言ってもホントは報酬目当てなんでしょ」と言われれば大抵の人は「いや、そりゃ、まあね」と答えるのが正直である、という風に言い表す事が出来よう。 これは、異性に対する下心に、例えられるべき物だと思う。 微弱な食い違い、というのは、社会全体に広く薄く現れているものではなく、鋭く局在している傾向にあり、件数として微弱であるが該当箇所での食い違いは微弱ではない。 何かの分野でチャンピオンに成る、みたいな場合というのが、それであり、これは丁度アファーマティブアクションのターゲットに成っている職位だろう。 公務員は、柔らかい意味では食い違いの局在領域と見なせるが、所得の安定性の観点から就職先として公務員を選ぶ人は多いので、報酬の期待値という視点で見れば、民間と同程度に報酬目当てである場合も多いだろう。 欲望として消費欲のみを考え生産欲を考えない、という事の他に、経済には、報酬は生産に要する苦労にではなく生産結果に対して支払われる、という特徴がある。 経済においては、報酬は生産結果に対応するものであって、あなたの仕事は楽しいのでその分報酬を安くしておきます、という計算は不正である。 生産者がこの権利を守る自己防衛策としては、生産者は‘鶴の恩返し’の様なやり方で生産過程を消費者の目から隠し、消費者には製品のみを見せる、という方法が有効だ。 その意味、労働の現場ではその権利が常時侵害されている、という問題がある。 私は、製造業の工場の単純作業員として働いていた時に、上司から「まだ体力に余裕が有るか？」という意味の事を聞かれて、それを実感した。 本来は、それを秘密にしておく権利が労働者にはあって然るべきなのだ。 市場で百円の卵を1つ買おうとするときに、売り手から「お金をもっとたくさん持ってますか？持ってるんなら(同じ卵1個に)もっと出してください」と言われた場合の事を想像し、それが如何に恐ろしい事かを考えれば、分かろう。 ヤマンバそのものだ。 苦労が大きいので報酬を高くしておきます、というのは、理解できるが、これも原理・原則からは逸脱しているのかもしれない。 労働市場の需給関係で、楽しければ就労したい人が多くなり賃金は安く成り、苦労が多ければ就労したい人が少なく賃金は高くなる、とは言えると思うが。 経済の公平性は、同じだけ供給すれば同じだけ報酬を受けれる、という公平性であって、同じだけ供給するのに必要な苦労には個人差がある。 その分は経済は何もしてくれないが、経済の公平性は、そういう公平性であり、私は、それを正しいと感じる。 苦労に対して報酬を支払わなければいけない、という事に成ると、今度は逆に、消費者の権利が侵害される。 そんな事をすると、生産者と消費者の両方の希望が折り合った所に価格を決める、という原則が成り立たなくなり、当たり屋的に(回避可能な苦労を故意に好きなだけ生産過程に挿入する事によって)生産者が消費者からぼったくれる様に成ってしまう。(参考：15日＠2007年11月＠日記) 生産の効率化の競争ではなく、生産を非効率にする競争が生じてしまう。 この事から消費者を保護する為にも、報酬は苦労に対してではなく生産結果に対して支払われる、という方式が妥当である。 そして、現実社会での取引態度には、ヤマンバの成分と、牛歩やアタリヤの成分の両方が含まれている事を、是正されるべき問題として、私は自分の経験と見聞きした話から感じ取っている。 アタリヤ成分としては、必要の無い残業をして残業代を受け取る、という慣わしが挙げられよう。 悪気の無い場合には、現実の労使関係では、ヤマンバとアタリヤが相いに他に対する防護策に成っている、と考えられる。 つまり、相手のヤマンバ代(しろ)を見込んで自分は予めアタッておく、相手のアタリ代(しろ)を見込んで自分は予めヤマンバっておく、という事が行われている、と考えられる。 そして、その事が、恣意的な要求線の前進と補給線の後退の隠れみのとして利用されている。 他の人がまだ働いているのに自分だけもう仕事が終わったからといって先に帰るわけには行かない、という言い分と組み合わせると、サッカーのオフサイドトラップ攻撃と同様の不正な攻撃方法を生む。 そもそも労働市場の競争の過酷さの何割かは、これに由来するだろう。 スキマの無い社会を目指す、という発言をネット上で見た事があるぐらいだ。 ただし、生産過程を消費者の目から隠す、という方法には、いわゆる手抜き工事の問題がある。 生産に、出来るだけ苦労が少ない事や、出来るだけ時間が掛からない事は、経済の問題だろうけれど、自分がどの仕事に向いているか、という事実に対して、どの程度それに自分が満足を感じるか、という事は、経済の問題ではない。 自分の仕事の内容の種類が下等だから自分は幸福には成れない、という不満を持つ人に対して、そんな事はありません、あなたがあなたである限り、どの仕事に就いても正当裡の報酬は変わらず、(正確には自分に最も向いてる仕事に就いた時に報酬は最大に成り)、その報酬で購入できる幸福の分量も変わりません、その意味では(いずれも報酬が正当であるという意味では)職業に貴賤はありません、お金では買えない幸福もありますが、いくら経済が万能だからと言って、そこまでは経済の力ではどうする事も出来ませんよ、という風に反論する考え方、これが、おそらく、公平性についての経済学の建て前だろう。 私は、これは間違っていない、と思う。 では、どこに問題があるのか、というと、経済の公平性というのは、あくまで、他人とのやりとりの公平性だけであり、人間の幸福は、それだけではなく、自分で自分をどう思うか、という事にもある事だ。 ナルシシズムを思い出すと分かろう。 経済学の公式教義における「職業に貴賤なし」は、報酬の正当性に関しての物だから、不当に報酬を得る職業を賤しいと評価する態度に対する否定でもないし、また、報酬の正当性とは別の視点からの貴賤観を否定する力を持つ物でもない。 経済学の建前とは食い違って、封建時代の価値観の人だけでなく、民法的な新しい価値観の人にも、職業に対する根強い貴賤観が見られる、という事には、自由競争から保護されている職種の保護されている事、に対する蔑視や、取引の公正さについて潔癖率が低かったり不正な取引の温床に成っている職種のその属性、を賤しいと評価するという、間違っていない態度も含まれているだろう。 報酬の正当性は自由競争に由来するので、自由競争から保護されている事は、マイナスポイントに成る。 自由競争から保護されている事による所得の増分は、名目上は稼ぎ取った物だが、実質上は、稼ぎの足りない分に対する公的補償金である、という見方も出来る。 しかし、公務員の職種の方が民間の職種よりもステータスが上である、という感じ方があるのも、事実だ。 これは、封建的な価値観だけによるものではなく、自由競争から保護される権利獲得のための競争という物があるから、という事なのかもしれない。 また、競争が激しいと不正に走り易い、という法則性もあって、激しい競争にさらされている職種の方が、その事によって蔑まれている場合もあるようだ。 向いてる仕事に就けていてもその仕事が何であるかによって満足度が変わる、つまり、職業には不本意なものから本意なものまでありその感じ方はほとんど客観的と言っても良いレベルに達している、という事を、第2種のアファーマティブアクションの存在は論理的に意味する。 この点は、証拠として重要である。 しらばくれられる事が多いから。 私は長年に渡って、アンコウの類から、お前そんなにこの仕事が嫌か、他人の仕事を馬鹿にしやがって、という態度を取られ続けて来たが、嫌に決まってるだろう、嫌だからアファーマティブアクションという運動が存在するんじゃないか、とぼけるんじゃない。 私はルールを守って正しく(嫌だとも言わず)それを避けようとしただけなのに。 この様な言い方は、自分で読んでも恥ずかしく成るが、それでも言わねばならない。 誰も言わなかったという事実は必ず悪用される、からだ。 ご飯にマヨネーズをかけて食べるか否か、寿司の舎利部分に醤油を付けるか否か、これらについて、好みの違う人は、お互いに、遠慮なく相手のやり方を馬鹿にする。 その際に、他人の食べ方を馬鹿にしやがって、という風に怒り出したりはしない。 どちらも、相手の意見に納得しないからだ。 この事から、他人の仕事を馬鹿にしやがって、という風に怒り出した人は、馬鹿にした人の意見に納得しており、自分の職業について馬鹿にした人と同じ様に馬鹿にしている事が言える。 これも、証拠である。 アファーマティブアクションは、受け入れ先のポストの業務内容を、そんなのただ甘い汁を吸うだけの仕事だから誰にでも出来るんだよ、俺にも吸わせろよ、といって馬鹿にする態度であり、その点も間違っている。 また、アファーマティブアクションは、他人の仕事を馬鹿にしやがって、と普段から言っている側の勢力が起こす運動であり、ここで欺瞞が露呈している。 ともかく、経済学的な公平性が貫かれていても、経済学の守備範囲が人間全体に渡るものではない事によって、不公平の問題は残る、という事だ。 それは、本質的には、自分がどういう人であるかの事実を本人がどの程度愉快だと感じどの程度不快だと感じるかが人によって異なる、という形での不公平である。 さらに、それは、そういう個人差の主成分は感じ方の違いではなく事実の違いである、という形での不公平です。 職業それぞれに対する万人共通の本意度に格差がある、という事と、機会の平等の正当性と、結果の平等の無理、に対するここまでの私の考えを前提にした上で考えるならば、そもそも不本意な職業に生来向いている人がそれ(自分が不本意な職業に生来向いている事)を不公平だと考えるのは当然である。 そして、それが不公平であるからには、正当裡の是正が不可能であるとしても、それはあくまで問題なのだ。 根底にあるのは、そんな仕事に向いてなんか居たくない仕事に向いている人に生まれて来る事の不幸と、そう言わせない事の理不尽だ。 前者は、適性と幸福感（自尊心も含む）の不一致、という言葉で言い表す事も出来よう。 適性と幸福感の不一致とは言っても、適性と幸福感は全く独立なわけではなく、むしろ、一致の不完全性、という言葉で表現する方が正確かもしれない。 神様は何故チョウチンアンコウなんて者をお造りに成るという酷い事をしたのだろうか、という意味の事を大槻ケンヂさんが言うのをテレビで見て、私はこの発言を大いに気に入ったが、この非常に気の利いた発言によって彼は、そんな仕事に向いてなんかいたくない仕事に向いている人に生まれて来る事の不幸、の事を言いたかったのではないか、という風に私は思っている。 チョウチンアンコウの不幸は、怪我でも病気でもない。 そう在るべくして生み出された何一つ欠ける事の無い全き健康と順調の内に良く本懐を遂げているその、「よし、その調子だ」という掛け声もカラカイの意味にしか解され得ない、一呼一吸一挙手一投足に至るまでことごとく侮りの対象と成らぬ物は無い、蔑視に対する防服を一糸まとわぬ姿での裸踊り、がチョウチンアンコウの不幸であり、それは正に不幸以外の何物でもない。 私が「あぁあぁ、目も当てられんわあ」と言うのは、この意味においてである。 会場で私は「高尚な問題」という言葉を使ったが、高尚な問題というのは、向いていたくない事に向いている人に生まれて来る不幸を何とかしてあげたい、という問題だと言える。 昔は、その部分が「優しさ」という言葉で表現されていた。 つまりは、あくまで与える側の任意の意志による問題だとされた。 だから、優しさという言葉が正党公約に登場して、それが要求される風潮が出始めた頃から、私は世相に不穏なものを感じている。 機会の平等への侵害という切迫した問題と高尚な問題を混同してはいけない。 故意に混ぜて煙に巻く事に至っては、以っての外だ。 なのに、それが蔓延している。 このページでは私は、向いていたい事に向いていない結果として向いていたくない事に割り振られる事を、向いていたくない事に向いている、という風に表現し、それによって問題を浮き彫りにした。 私が子供の頃は、向いていたくない事に向いている人に生まれて来る不幸は戦争の悲惨さに比べればまし、という風に教えられ、それに心から納得した。 平和な世の中で優れた人と劣った人が馬鹿にし馬鹿にされながら共存している様は、微笑ましいものに感じられた。 しかし、平和が当然の大前提でこの歳まで生きてみると、平和の中の小さな不幸も、なかなかなものに感じられる。 機会の平等への侵害は人による不公平であり高尚な問題は神による不公平だ、と言える。 人に出来る事は、人による不公平の是正のみである。 これは単に人間の能力が足りない、という意味ではなく、人の手によって是正する事はそれ自体がもっと不公平な行ないである、という意味の、深刻な原理的な不可能を表すものである。 生来の性質はその人の責任ではないから、という理由でそれを無いものとして扱う事は、悪を生来の性質として持って生まれて来た人を考える場合に、ボロを出す。 この場合には、生来の性質だから罰する事はしない、という態度が、被害を受けた人に対する不正行為である事は、明白である。 ---↓枝葉末節↓--- 神による不公平を人の手によって是正する事はそれ自体がもっと不公平な行ないである、という事を、以下で詳しく説明します。 (1)禁止による是正。 お前の結果は良過ぎるから、という理由で、結果に手を触れてそれを押し下げられた者は、大きな苦しみを感じる。 押し下げるその行為が不公平だからである。 一方、もともと自分の結果がそれだけだった者には、そういう苦しみは無い。 したがって、押し下げた結果も、また不平等である。 もともとの結果が低かった者にも負の感情(落胆や意気消沈や悲しみや自尊心の傷付きや恥ずかしさ)は生じるが、それは、結果を押し下げられた者の感じる苦しみ(被奪感や被殺感や不条理感や怒り)とは異なる種類の物である。 両者の違いは納得の有無であって、大小が問題なのではない。 結果へ直接介入しそれを改変する、という行為が無い場合には、結果の良かった者は嬉しく、結果の悪かった者は悲しい、という不平等が生じるが、この神による不公平に対して、結果へ直接介入してそれを改変する、という人の手による是正を行なうと、今度は逆に、結果を押し下げられた者だけが苦しむ、という、元々の不平等よりももっと笑えない不平等が生じる。 その様な是正は不公平である。 この事は、生来の腕の本数が普通は2本だが希に3本の人も居る、という状況を仮想すると、分かる。 この比喩を充実させるためには、3本腕のピアノ演奏家が3本腕のためのピアノ協奏曲を演奏して大きな経済的成功を収めた、という状況を仮想するとよい。 3本腕の人が、お前のは多過ぎるから、という理由で腕を切り取られたなら、切り取られた人だけが損を強いられた事に成るのであって、その恨み(納得できない気持ち)は残存し、腕の本数は平等に成っても、総合すると、結果は決して平等ではない。 持って生まれた命の一部を勝手に捨てられた、という被害の有無の分だけ、結果は不平等である。 良い喩に成るかどうか分からないが、手や足を丸ごと一本切除すると、その後、夜な夜な、もう無いはずの手や足がまだ有ってそれをどうしたらどうなった、という悪夢を見る、という話を聞いた事がある。 切り取られなかった人には、そういう苦しみは生じない。 切り取った後で、2本腕で演奏しても3本腕で演奏したのと同じ音が出るピアノが発明されるなどして、腕の本数への社会的注目度が低下し、しかし切り取られた本人にとっての腕の本数の価値は変わらない、という事は有り得る。 その場合、「ああ、ごめん、ごめん、別に切り取らなくてもよかったね」では済まない。 現実の社会で見掛ける、危険だ、失礼だ、病気だ、協調性が無い、文化に反する、ブルジョア的だ、等の理由は、腕が多過ぎてはいけない理由が無いものだから、切り落とす為にこじつける理由に例えられよう。 この場合、腕を切り取られたり切り取られそうに成った人が、その後で、2本腕の人の腕の本数の少なさをどんなに蔑んでも、その事に呵責を受けるべき罪は微塵も無い。 私の言動は、この道理に基づいている。(会場での言動の事ではない) 私は無神論者ですが、比喩的に言うならば、天才に生まれた者にとって、才能の開花というものは人生の第一であって、それを通したいなら孤児として出生してもらうと、もし神に言われたとしても、才能の開花を選ぶ様な事だ。 これは、二者択一の前提を置かずに孤児でも良かった、という意味には成らない。 それは、右目よりも左目の方が大事だという主張が、右目を潰されても構わない事を全然意味しない、のと同様だ。 この事情は、非天才には無いものだから、才能の開花を皆が我慢しているのにお前だけ我慢しないのは我儘だ、との批判も妥当しない。 私は、ガソリンに生まれたのに薪の様に燻らされて来た、と感じている。 これは腕を切り取られた事に等しい。 堆肥燃料の奴らの仕業に違いない。 私は日頃、自分が音楽等について何を好むかが批判の対象とされている様に感じ、その事にも怒っている。 何を好むかは善悪の問題ではないからだ。 (2)補給線の後退と要求線の前進による是正。 結果に手を触れる、というやり方以外に、私が、補給線の後退と要求線の前進、と呼ぶ不正が存在する。 結果が良過ぎる者への金銭や物資の補給を不当に減らすのが補給線の後退で、結果が良過ぎる者に課す義務を不当に増加させるのが要求線の前進だ。 このやり方では、ターゲットが、補給の減少分を自分で補ったり追加された義務を果たす事に、時間や労力を奪われて、その分だけ結果が低下する。 これを結果が並に成るまで行なう、というものだ。 補給線の後退と要求線の前進は、妨害という概念を四角四面に言った物だと言えよう。 ゴルフのハンディキャップは要求線の前進に該当するが、優劣の事実に被せるものではない。 ハンディキャップの分量が明示されての事なので、その値と結果からハンディキャップ無しの場合の結果を算出できるからだ。 実利的には(獲得賞金については)そういう事情は成り立たないが、プロゴルフにハンディキャップは無い。 プロゴルフにハンディキャップが無い事は、私の主張が既存の正義感に一致している事の一つの証拠と見なせる。 所得への累進課税制度も要求線の前進の一例だが、これについては、与益量に対する所得額の反応が線形ではない事に基づいているならば、その限りにおいては、私はこれを正しいと思う。 しかし、誰かが勝手に金持ちに成り過ぎない様に、という事なら、これは私の基準では不正だ。 (3)選択を誤らせる詐術による是正。 騙して自分で捨てさせる、という手口も存在する。 3本目の腕を「もともと無いんだから探すな、あるわけないじゃないか」と言われて、本人が誤って「それもそうだな」と思ってしまう事を狙うやり方や、事実に反して、他の人もあなたと同じぐらいに優秀(腕は3本)だよ、という情報を与えるやり方がある。 他の人も腕が3本なら、3本腕を活かした仕事は、わざわざ自分がやらなくても他の人に任せればよい、とか、職位獲得競争で勝てる見込みが少ない、と考えて、本人がそういう進路選択を自ら放棄する確率が高まる。 私に対しては、これら両方が併用されて来た、と思っている。 自分には3本目の腕がある事を本人に気付かせない様に工作した上で、それと同時に、親切や良識を装って、探さない様にそそのかす手口だ。 私の場合「何か変だな、どこか誤魔化されている感じがするなあ」という気持ちを何十年も持ち続けて来た。 しかし、それを証明するには「お前ら嘘を吐いてるだろう」という風に問い詰めて白状させるやり方では証拠を提出できないので無理だ。 私が歴史に残る様な学問的業績を打ち立てようとしたのは、その証明のためでもあった。 打ち立てる事が出来れば、やはり誤魔化されて来たのだ、という事に成る。 騙す側は、そんなのは土台無理な話である事、に依拠して、それに満たないが非凡な才能を揉み消そうとする。 そして、おおよそ文法物理学というものを考え出す事が出来た時点で、やはり何十年も騙され続けていたんだ、という事を私は確信した。 現時点で既に、私がこの道を歩むに値する人間であった事は十分に証明されたし、私の学説の急所の的中が確認されれば、間違い無く私は「ニュートン、アインシュタイン、ハイゼンベルグ、シュレディンガーの次は誰ですか？」という問いの答えに成る。 騙して自分で捨てさせる、という手口の被害に遭った場合、捨てた後で抗議しても、その時には、元々は有った、という事を証明できない状態に成っている。 この見地から、捨てずに‘して見せる’事によって才能を証明する事は、逸失させられそうになった利益の存在の証明としての意味を持つ。 それ無くしては、有るわけないから無かったのだろう、という主張が通ってしまう。 死人に口無し、と同じだ。 騙して捨てさせる行為は、当然この原理に依拠していて、将来自分が断罪される恐れはない、との卑怯な計算に基づいている。 この意味でも私には、‘して見せる’事が、是が非でも必要だった。 私自身、自分は天才ではないのではないか、と疑った事もある。 普通は、疑う、ではなく、自信を無くす、と言うのだろうけど、私の感覚は、疑う、という言葉が適当であるほど、客観性を帯びている。 才能の自覚はその様にデリケートなものだから、斜詭な助言を弄してその感覚を攪乱すべきでない事は、針に糸を通している人の体に当たるべきではない事と同様だ。 自分を励まし鼓舞して困難な善い目標を達成しようとするのを挫く事に、何の正当性が有ろうか(反語表現)。 その分、捨てさせようとした者が、捨てずに‘して見せた’者に、失礼とか有害と言って難癖を付ける事は、「よくもまあ抜け抜けと、盗っ人猛々しいとはこの事だ」と言われるべき呆れた態度であり、これは、言うべきではない事を言わなければ通れない様にする通せん坊の例、と見る事も出来る。 騙して自分で捨てさせる、という手口の被害に遭った場合、被害者は、本当に自分には才能が有ったのか、証明できなく成るだけでなく、自分でも確信を持てなくなる。 つまり、これが、口の無い死人の状態である。 それに対して、本人の意に反して、それは危険だから、などと理由をコジツケて、3本目の腕を強制的に切除した場合には、本人には、ハッキリと、元々は3本目の腕があった、という事が判明している。 その様な場合ですら、切り取った後で「いや、お前の腕の本数は、もともと2本だったんだ」という風に強弁する、という性質が、切り取る側の人にはある、という事も、私は見て来た。 (4)強奪し破棄した上で元から無かったと白を切る事による是正。 私は、十数年ぐらい前に、精神病だ、という風に言われて、抗精神病薬を飲み始めた。 その際に、薬を出した医者から、抗精神病薬を飲むと便秘および肥満が生じる、という説明を受けた。 そして、その様に成った。 その後、何年も経ってから、父や友人にその事を言うと、抗精神病薬が肥満の原因に成る、という事実を認めようとしない態度が返って来た。 つまり、これは、やせ形だった私を薬で太らせた後で、お前はもとから太っていた、という風に強弁するパターンに該当する。 そうとは限らない、と思うかもしれないが、同じ病院に掛かっている友人に、私の元の体重が65kgであった事を知らせた際に、その友人から、その事実をしつこく否定され、それでも私が、そうだったものはそうだったのだ、と言うと、その友人は、顔面を引き攣らせてムンクの叫びの口を閉じた様な表情に成った。 これを見た時に私は、自分の劣等感を他人に償わせようとする邪な意志が、これまでの私の境遇に大きく反映されていたらしい、と強く感じた。 先日、映画館で「世界にひとつのプレイブック」という映画を見た際に、登場人物の会話の中に、抗精神病薬の名前を具体的に挙げて、この薬は太る、という風に複数の人が述べるシーンがあった。 これは、抗精神病薬が肥満の原因に成る、という事実および、その事が周知の事実である事、の証拠と見なされる。 服薬中は、私の体重は少なくとも84kgまでは増えていた。 服薬前の私の体重が65kgであった事は、私の著書「古典物理学」の380ページに書かれており、そこに掲載されている写真およびウェブ上の著者情報ページに掲載されている同一の胸像写真から体形は痩せ形である事が、ハッキリと分かる。 この本は、私が1999年に執筆した物だ。 私は、肥満は嫌だ、とは思うが、もともと自分が肥満だったなら、ここまではこだわらない。 事実と違う事を言われているから、それも、そう言うために前もって必要も無い薬を飲ませての事だから、烈火の如く怒っているのだ。 それが何故深刻な問題であるか、というと、極端な話、私が私本人である事を証明できなく成る、という事態に繋がり得るからだ。 そして、その事も狙われている、と感じるから、看過できないのだ。 これが、本人の目の前で切り取っておきながら後で元々無かったんだと強弁する行為の私による被害実体験である。 肥満云々以前に、精神病患者に仕立て上げる、という事が、本人の目の前で切り取っておきながら後で元々無かったんだと強弁する行為である。 1995年に千葉県から広島県の実家に帰った際に父から、大学に行く前は理屈っぽくなかった私が大学に行って理屈っぽく成った、という風に言われ、おや、と思った。 これについては、その後何度か父に再確認したが、やはり、父は同じ事を言った。 事実は、私は、幼少の頃に、手当たり次第に父に、あれは何故なのか？という風に理由を尋ねて父を煩わせた、という事があったほど、理屈っぽさは幼少の頃から今に至るまで一貫した私の固有の性質だ。 今でも(不調の根本も周囲の人の態度も)改善されていないが、私が周囲の友人や親族や医者に身体の不調を訴えると、その内容を否定しようとする異常に強い傾向が、それらの人に見られる。 学生時代に、下宿の友人に、何だったか、自分の身体の不調を言うと、全くもって不可解な事に、その友人は、それに対して立腹の様相を呈した。 今から何十年も前であるその頃から、そういう傾向が出ていた、という事だ。 これも、自分に関する事実を否定される、という点で、上記と共通している。 学生時代に同じ下宿に住んでいたその友人は私に、認められるのは死後でもいいですか、という風に打診した事がある。 それが、私の過剰な自意識をからかう為に故意に話を合わせる類の軽口ではなく、真面目な打診のニュアンスを帯びていた事は、今ここでは伝え様が無いが、そうであったので、これは不審な出来事の一つだ。 私が歴史に残る様な業績を樹立する確率を、常識では考えられないぐらいに、そしてまた私自身もそこまでは思ってなかったぐらいに、高く見積もった上での発言、だと思われるからだ。 その友人は文科系の友人だったので、私の将来性など分かるはずなく、それだけ、なお不審である。 そして、私が生前に認められる事はある範囲の人々にとって(おそらく経済的に)都合が悪く、その人々の手先として、私から権利放棄の約束を取り付けよう、という意図が感じられたからだ。 私が偶然に思い付いたアイデアをメモした「物理学の偶発的方法」というタイトルのノートを見せた時のその友人の反応も、不審だった。 公開するのはけしからん事だが貴様それを分かっているだろうなあ、という意味で「公開するつもりでは無いんだろう？」という風に聞かれ、公開するつもりは無い旨を答えると、「うん、それならいい」みたいな事を言われたからだ。 公開するのはけしからん事ではないので、不審である。 また、そのノートでの私の斜線／を用いて項目を アイデア1／アイデア2／アイデア3／・・・ という風に区切る筆記法を、その友人はその場で(1990年頃)褒めたが、その後(2000年以降)、大人気のインターネット掲示板の各ジャンルのトップページでのスレッドタイトルの区切り方が、それと同じであるのを見て、不審に思った。 不審打診について、最近では、数年前に、中学時代の同級生が遊びに来た時に、私の現状の経済面を理由として、経済面に限定せず現状に満足ですよね？という風に打診した。 これについて私が不審に思っているのは、何かを私に伏せて話をしている、と感じる点だ。 ピカソの絵をそれと知らずに持っている人に、その事を知らせずにその絵を千円で売ってくれませんか？と持ち掛ける様なニュアンスを感じた。 満足か不満かを決める私の基準は、結果単体に課せられるものではなく、私本体と結果の関係に対して課せられるものだ。 例えば、経済活動については、私本体が私の収入と支出の現状以下ならば、現状でも多過ぎる、と感じるし、私の収入と支出の現状が私本体以下ならば、現状では少な過ぎる、と感じる。 それを、収入と支出だけ見て、多いか少ないか、と聞かれても、答え様が無い。 ついでの話、結果の平等という考え方は、この点についての不理解である。 私本体への評価が非常に高い、という事実が背景にあって、それを私に告げた上で質問すると私が不満だと答えるので、その事を伏せて、現状に満足です、という答えを引き出そう、という意図が感じられた。 伏せて話す、という行為の不当性は、リスクについて十分に説明せずに投資を勧める事が不正行為だと見なされている、事を見れば分かる。 これは(3)に属するだろう。 (5)存在しない禁止を存在すると思わせその事を隠したまま別件で賠償する方式の是正。 進路選択について言えば、伏せて話す事は、次の寓話で表現できる。 二岐で片側を工事による通行止だと偽り、反対側に行かせた後、その事を知らせず伏せたまま、弁償として金品を与え、今の状態に満足ですか、と尋ねる。 満足か否かは結果の実益の量で決まるものではない。 結果が悪くてもそれが自分の選択の結果なら不満に思わないし、結果が良くても自由な選択が妨げられたなら、不満に思う。 自由を重んじる、というのはそういう事だ。 選択の自由を奪った後で、不満ならもっと増やしましょうか、と言う態度も、何も分かっちゃあいない態度だ。 自由な選択が妨げられたなら、いくら増やしても不満は解消されないのだ。 自由な選択に従えば、もっと大きな結果が出たかもしれない。 私の態度は常に、成り得る限りの者に成り為し得る限りの事をする、という物です。 従って、私に選択を訊く時には、この場合にはそれは具体的には何に成りますか、という質問か、これですか、という確認の質問しか有り得ず、あなたの欲深さはどの程度ですか、という質問は、最初から有り得ない。 そういう質問に敢えて答えるなら、無限です、というのが私の答えだ。 (6)言質の曲げ取りによる是正。 いつ頃からか私は、そうやって答える事が出来ない様にした上で、どうですか？と聞いて来る質問を受ける様に成った。 ある時、現業労働者と思われる2人組の内の1人が、うっかり何か私に尋ね、私が答えると、もう一人が、私の答えが気に入らなかったらしく、だからこいつに訊くなと言っただろうが、という風に尋ねた人をたしなめるのを見た事がある。 歯科医で治療を受ける時には、口の中に物を入れられてしゃべれない状態の時に、質問される、という嫌がらせを受ける。 口の中に物が入ってない時に質問してくれ、と要請しても、持続的な改善への意志が感じられず、何度も同じ目に遭う。 冒頭で述べた様に、私は、自分を取り巻く環境に対して、心頭に発するぐらいに怒っているのであり、その事をその友人が分かっていないはずがない。 私の場合、収入の名目が間違っている。 私の現在の収入は障害者年金というもので、これは、あなたは普通の人よりも劣っているので、その劣った所をこのお金で補ってあげましょう、という名目のものだ。 また、物理学で世界一の業績を上げても経済的に親の面倒を見る力が無い、なんて事が有るだろうか(反語表現)? 私は、そういう状態に封じ込められている。 こんなのは、あなたが他人に恥をかかせた分だけあなたにも恥をかかせます、という単純に犯罪、腐れ結果の平等である。 結果の平等が必然的に不正を必要とする、という事は、ここにも現れている。 この状況を私が満足だと感じるはずがない。 依頼を断る際に婉曲な表現を課して、相手の拒否表現を曖昧にして受容の意味だと曲解出来るようにしたり、婉曲表現作文の難しさを利用して、断る権利がある事項なのに、作文問題を解けなければ断る事が出来ない、という状況を勝手に設定したり、言い難い雰囲気を作ったり言えない様にした上で、言わなかったから黙認した、という忖度(そんたく)をこじつける事も、言質の曲げ取りに当たろう。 言葉狩りもその道具だろう、と私は睨んでいる。 言質の曲げ取りの汚さに比べれば、何でもズケズケ言う図々しさなんて、全く失礼でも何でもない。 認められるのが生前か死後か、という打診についてもそうだし、生活の現状に満足か、という打診についてもそうだが、コントロールしてはいけない事をコントロールする意志の存在が感じられる。 この点が両者に共通の本質的な不審点だろう。 評価機能を担っている人は、私の仕事を見て素晴らしいと思えば、素晴らしくないと言ってはいけないのだし、見れば素晴らしいと思うかもしれないから見ない様にする、というのも不正である。 それなら宇田の仕事を見たらそれを素晴らしいと思いそうな人を宇田の仕事が見える位置に置かない様にする、というのも、不正である。 何処をどう工夫しようが、コントロールする事を目的になされた行為は全て不正なのだ。 相場を操作する目的での取引は不正である、という既存の正義と同様である。 生前に認められるか死後に認められるかは、人が決める事ではなく、自然な成り行きに従って決まる事なのだ。 従って、私は死後でも良い、と答えたと思うが、これは、それなら生前には認めない様にしよう、というコントロールを容認するものではなく、自然な成り行きに従って決まった結果が死後に認められる事であっても構わない、という意味に過ぎない。 デブでも構わない、についても、同様である。 先述した初診の精神科医は私に、頭の良い人もそれ相応の地位に就かないならば頭が良い事を主張してはいけない、あなたには馬鹿に成ってもらう、という風に要求した。 余りに論外なので信じ難いと思うが、そう言ったのだ。 頭が良いか悪いか、というのは本人の固有の性質であって、頭の良い人が馬鹿に成る事は出来ない、馬鹿の振りをする事は出来ても。 それは、ぶん殴ったり毒を飲ませたりすれば馬鹿に成る事もあるだろうけど、おい、それは治療ではなくて傷害だろうが、暴力だろうが。 この精神科医は、ぬけぬけと私にそう言ったのだ。 そして、薬を飲んで馬鹿に成れ、と言っているのだから、これは、毒を飲ませて馬鹿にする、という事だ。 その後、この医者個人に限っては態度に問題がある、という意見を聞いたが、これはトカゲの尻尾切り的な言い訳だろうし、それも、言葉に信用力の無い人からだ。 言い訳すらそういう人(言葉に信用力の無い人)に言わせる、という逃げる気満々の態度である。 私は、患者にそういう論外な要求をする事が、その医者個人の傾向ではない事を、ハッキリと感じ取っている。 何が言いたいか、というと、私が言いたいのは、自由競争を否定する、というのは、その建前の美辞麗句とは正反対の、この様な、どう繕っても繕い切れるものではない犯罪に直結する方針だ、という事だ。 錯覚ではない才能の自覚の存在は、数学の難問に対する「あ！分かった」という感覚になぞらえると、明瞭に理解できる。 数学の難問、客観的に難問でなくても良い、自分にとっての難問で良い、数学の難問を解こうとして長時間考えたが解けない、そしてある時「あ！分かった」と感じ、それから、その感覚に導かれて紙に図や式を書いて計算すると出来た、という経験の事だ。 この「あ！分かった」という感覚は、間違っている場合もあるが、当たっている場合もある。 そして、「あ！分かった」と感じた瞬間には、まだ他者に、自分が分かったという事を証明して見せる事も、何がどう分かったのかを説明する事も、出来ない。 つまり、この感覚は解けるという事実に先立って予見的に現れるものなのだ。 自分には才能がある、という感覚もそうである。 間違っている場合もあるが、そういう事を言う奴のは全部錯覚だ、というのも間違いだ。 非凡な才能を証明する業績を樹立した者で、それに先立って自分の才能の非凡さを自覚していない者は居ないはずだ、と私は確信している。 そして、そういう人の「あ！分かった」に例えられる形で現れる才能の自覚は、本人にとっては絶対に間違ってない事が明白なものである。 私が今まで感じて来た圧力を一言で言うと、はっきり、お前のそれは他のみんなは持っていないので捨てろ、だった。 他のみんなは持っていない、では、捨てろと要求する理由に成らない。 親切な助言の形式を用いての、自分は特別だと思わない方が良い、というイヤラシイのもあった。 これは、MAYとMUSTのすり替えによる詭弁の亜種だ。 良いって、誰にとって良いと言ってるのか？ その助言者には、自分にとって良い事を、私にとって良いかの様な言い方で言うな、と言いたい。 私がその口車に乗せられて才能の開花を目指さなかったなら、文法物理学は誕生していない。 その助言者には「お前、その責任を取れるのか？良いわけないだろうが、私だけの問題ではない、社会にとっても損失だ、良いのはお前だけだろう」と言いたい。 それでも構わないんだ、という考えは、物事の順番に対する呆れた無視だ。 私に対して、自分勝手という批判をする者は、だいたいそういう自己中心的な人だ。 悪意が無く、私の才能を認識できなかったための助言だったとしても、どの様な重大な結果をもたらすかに無頓着な軽率で無責任な助言だ。 それですらそうだから、悪意がある場合には、悪質極まりない。 その場で反論すると、こっちがものすごく格好悪い、という点を計算に入れている所も、イヤラシイ。 私の場合、騙して自分で捨てさせる手口には、私の親まで手先として動員されている。 そんな事は無い励ましたじゃないか、と反論するかもしれないが、優秀レベルまでは励ましだが、それを越える分については否定だった。 よくある、おだてられて調子に乗ってる奴、という批判のたぐいだ。 そういう経験をするたびに、キツイお灸として逸失利益の証明がやはり必要だ、と痛感した。 独創的なアイデアが生まれる事は、子供が生まれる事と同じだ。 したがって、アイデアの帰属先が、発案者に、である事は、物財の帰属先が、所有者に、である事よりも、遥かに自明性と正当性が強い。 その分、それを揉み消す事は、被害者に大きな不条理を感じさせる。 我々の社会では、所有権という物を大切にし、それを少しでも侵害したなら直ちに泥棒と叫ぶのだから、アイデアの帰属先を誤魔化す事は、それ以上に泥棒である。 私は現在、精神病だ、自分は天才だという考えは誇大妄想だ、という難癖を付けられており、これは、思想内容の強制であり、騙して自分で捨てさせる、の延長上にある。 捨てろと言ってそそのかしても捨てなかったので直に手を触れて棄損に掛かって来た。 ここまで来ている。 誤解された人の「違うんだ、違うんだ、俺はちがうんだ」という態度ならまだ分かるが、私に対しては「違うんだ、違うんだ、お前は違うんだ」が来た。 ここまで来ると、もう、精神が限界に達しているのは、こういう態度の人の方だと思うが、現実の厳しさに耐え切れなく成ってる状態でしょ。 天才だから特別扱いしろ、と言ってるわけでもない事は、22日＠2007年12月＠日記＠宇田英才教室に書かれています。 私には、要求線の前進の事を、「くべる」という言葉で表す事がある。 これは、出力が等しく成る様に入力を決める不当行為を、炎の具合を見ながら薪をくべる行為に、例えての事だ。 結果を平等にしようとすれば、機会が不平等に成る。 神による不公平は人の手では是正不可能とは、神による不公平を是正するためには人による不公平に依るしかなく、そちらの方がもっといけない、という事を、ここまでで、具体的に説明しました。 この様な話は、書いている私自身、気持ちの良いものではない面がある。 その事に付け込んで、ここをほじくり返せば、世の中のとうの昔に既に一応の収まりがつけられた問題を再燃させ、色々な事を曲げる事が出来る、という風に考えて実行した者が居て、それが諸悪の根源だと私は勘ぐっている。 思っていても言いたくない事、言うべきでない事、というものがある。 それを言わなければ先に進めない様な状況を当てがって通せんぼする嫌がらせがある。 言いたくない事を言わせれば、恥をかかす事が出来る、言うべきでない事を言わせれば、非難をコジツケる事が出来る、両方を避けたい者は引き返させる事が出来る、という寸法だ。 もちろん、そんなやり方に正当性は無い。 発言が無遠慮だから、という理由で将来何かの賞をもらえなく成るとしても、私には、ここに書いた様な事を言うのを差し控えるつもりは無い。 私は、腹いせだけで言っているのではなく、正義感でも言っているから、その様な犠牲を払ってでも言わねばならない、と感じている。 そうやって誰も何も言わないから、いつまで経っても同じ事が繰り返されるのだ。 そして、不正を行なう者達は、それについて発言の遠慮を求める事を、今後もずっと不正を行ない続けるための手段としか見ていない、という事を知るべきだ。 この負の連鎖を何処かで断ち切る必要が有る。 ---↑枝葉末節↑--- 以下しばらく、勝つなという要求の不当性に、話を戻す。 尋ねられての事だったか、会場では私は、機会の平等とは大雑把に言うと試験を受ける権利の事だ、と述べた。 少し手直しすると、試験を受ける権利が全ての人に等しく与えられている事だ。 何を言いたかったかと言うと、合格した場合の処遇を全ての人に等しく与える事ではない、という事だ。 合格した場合の処遇を全ての人に等しく与える事は結果の平等である。 それ以外の点については、この定義は大雑把過ぎて正確ではないので、その点を、ここで補足説明したい。 勝負し、その勝負に対する公正な審判を受け、その結果に応じた処遇を受ける権利が万人に等しく与えられている事、という言い方も出来ると思う。 何でもかんでもではないが、勝負してもよい事が例外的にあるのではなく、勝負してはいけない事が例外的にある、という具合に、勝負してもよい範囲が非常に広い、という事だ。 勝負する権利というのは、経済競争の場合には、市場への参入の自由、経済活動の自由に他ならない。 言ってる事の正しさや優秀性の競争については、言論・出版の自由だ。 芸術などについては、表現の自由だ。 これらは法律によって肯定されている。 言論、出版、表現については、表現された人の権利との折り合いからではなく、表現者同士の、どちらの表現の方が優れているか、という競争の観点から、自由を制限してはいけない、というのが機会の平等の考え方だと私は心得ている。 つまり、誰が誰に対してであれ、俺より優れた事をするな、という要求をする事は不当だ、との認識だ。 この、くすんだ者が光る者に被せる、不当な要求は、滑稽な事に大体、俺より優れた事をするな、なぜなら俺の方が優れているからだ、という論理を背景にしている。 心配するな、お前の方が優れてるんだったら、お前よりも優れた事なんか出来やしないから。 ボクシングではチャンピオンが個々の挑戦を拒否する権利を持つ。 私は、これを、勝負する権利を否定しているからいけない、とは考えない。 しかし、いくらチャンピオンでも、チャンピオンの輝きを相対的にくすませるぐらいに輝く事(ボクシングであっても構わない)を他の誰かが独立に余所で行なう事まで禁止する事は出来ない。 隣で風船大会を開いたらボクシングよりもそっちの方が格好良かった、という事がもしあってもだ。 勝負する権利が肯定されるのは、この意味においてである。 自由に勝負する権利は、それに依拠して放逸さの点で無制限に自分のしたい様にする態度への、それは良い所取りだ、という批判については、良い所取りが評価のみについてなら、それは批判の対象とは成らない、という事を含意する。 スポーツの競技で三冠とか五冠を達成した人は、他のプレーヤーから何か取ったのか？ 取ってはいない。 私に関して言うなら、私に対して批判の意味を込めて「良い所どり」と言う者に対しては、「まるで自分にも出来たみたいな言い方じゃないか」と反論したい。 研究職ではない人Aが研究職の人Bのお株を奪う様な業績を上げる事は、AがBの仕事を取った事には当たらず、それまでBがAの仕事を取っていた事が立証された事に当たる。 BがAを退けてその職に就いた時点でBがAからその仕事を取った、と解釈するのが正しい。 つまり、それは、第一義的には、Aの不徳ではなくBの不徳であるのだ。 そこまで厳しく言わなくても良いじゃないか、とは言えても、それをAの不徳だと言う事など言語道断、盗人猛々しい、開き直り、甚だしい責任転嫁である。 この様な考え方は、実力主義という言葉が盛んに用いられていた頃には、暗黙の了解として、行間に潜んでいた。 この様な考え方が私個人の捏造物ではなく文化として広く受け入れられている事、を示す例に、道場破りという物が有る。 道場破りは、武道の道場に外部者が訪ねて来て道場の先生に試合を申し込む習慣の事だ。 武道の道場を営んでいる者は、入門者には、時期が来るまでは相応の試合を許さない。 しかし、道場破りは別だ。 いやしくも道場を開いて先生を名乗っているからには道場破りには応じねばならない、というのが道場破りの考え方である。 そして、道場破りの方が勝った場合には、それは、道場破りが悪い事をした、と解釈されるべき事ではなく、それまで先生が(実力不足のくせに先生を名乗るという)悪い事をして来た、と解される事なのだ。 それでは、世界一でなければ道場を開いて先生を名乗ってはいけないのか、と言うと、もちろん、そんな事は無い。 おそらく、道場破りの論理は、看板に偽りあり、という悪への罰と抑止と除去であろう。 私は先生としてそんなにレベルが高いわけではないがそれでも私よりもっとレベルの低い人だってたくさん居てその人達にとっては十分に先生だからそういう需要に応える道場を開いているんです、という場合には、その態度に非難される余地は全く無い。 まず排除しておいて、排除された者が奪還する事を、他人の仕事を取る、と言うのも詭弁だ。 職位の獲得が公正な競争に基づかない場合は、この論理の適用を免れない。 既得権益の保護にも二種類ある。 二者が納得づくで同意して結んだ契約を、後で当事者の片方が他方の意志に反して一方的に解約する事は出来ない、という意味が一つ。 もう一つは、由来は色々あるでしょうけど既成事実の維持はそれへの変更よりも優先される、という考え。 どちらも、それなりに妥当性はあるが、後者については、それを良い事に不当に既成事実を作るならば、妥当性を失う。 つまり、後者は、由来が正当でなくても既得権益として認めよう、という考えだから、極端な話、今は俺が持ってるんだから、という理由で、泥棒は持ち主に盗品を返さなくてもよい、という考えに通じ、それを当てにして先手を打って盗んだ結果の状態には正当性は無い。 これは、理屈のための理屈ではなく、現実に領土問題で横行しているのは、まさにこの手口だ。 職位についても、就職・採用の段階で何とか誤魔化して有能な者を退け、後は何を言われても既得権益の一点張りで押し通す、というやり方は、これだ。 良いとこ取り、という批判を検討するに当たっては、そもそも学者という職業が他の職業に比べて良いとこ取りだ、という大前提を忘れてはいけない。 学問内での自由競争を否定する事は、自分が自由競争によって学者の地位を獲得した事の正当性、という自らの寄って立つ基盤を否定する事である。 学問の自由についても同様である。 職業学者以外は学問の研究と発表をするな、という態度は、政治権力が学者の研究に圧力を掛ける事と何ら変わらない。 また、自転車レースで、集団に埋没したまま体力を温存する選択と、一人だけ集団から飛び出して先行逃げ切りを図る選択の、どちらが得でどちらが損というわけではない事も、引き合いに出されるべき事である。 自転車レースで集団から飛び出して1位に成った人が、ズルをして勝った、と評価されるのではなく、それだけの者だったのだ、という風に評価されるのは、勿論の事だ。 俺は盗ってなんか居ない。 いつまで経っても誰もしそうにない事を十分に確認した上で与えてるんだ。 これが、競り合うな出し抜け、の思想だ。 また、もともとは、私は単科での成功に甘んじるだけの譲り合いの精神を持ち合わせていた。 それなのに、お前は物理は出来るかもしれないが社会科はできない、みたいな批判をする者が出て来た。 これが批判ではなくて侮辱なら、大目に見る寛容さも、私は持っていた。 具体的には、私の選択しなかった分野への無知を利用した通せん坊が仕掛けられる、という事が続いて来た。 心理学や経済学や医学や法律が、それである。 物理学以外の分野の仕事に接した時には「いや～、これは、なんとも、立派な仕事ですな～」と言って、感心して見せる事も、もともと私には出来る。 私が選択しなかった分野を選択した人が、宇田には出来ないが俺には出来る、と言って自分を慰めるのも、どうぞご自由にだ。 しかし、私に、それをやれ、と言われたら、話は別だ。 そして、そういう要求が、隠然と、私に突き付けられ続けて来た。 物理学での私の前進を妨害する目的で、である。 つまり、義務を何とか御してさあ物理学での歩みを進めるぞ、という段に成ると義務を上乗せして来る、というパターンだ。 正確には、勿論そういうのは義務ではなく、義務ではない事を義務だと言い掛かる屁理屈で私の進路を塞ぎ、それが義務ではない事を私が立証できない様に、立証には私が選択しなかった科目の知識が必要な様にしてある、という事だ。 だから、私は、物理学以外の他の事もやる様に成っている面がある。 そうして私は、宇田経済学や相対正義論を作り始めたが、これらは、経済学と法学の最も良い所を取ってしまうだろう。 他人のテリトリーを侵している、という意味で、良い所どり、と言うなら、これが反論だ。 良い所取り、という批判への反論を一言で書くと、良い所取りは悪ではなくまた盗ったわけでもない、という言い方に成る。 悪ではない、という点については、傲岸街道一直線は有りどころか誰もが出来るものならそう在りたいと考える模範・理想だ、という先述した私の認識の所で既に述べた。 他人の物を盗ったわけではない事の説明は、直上で詳しく行なった。 この事を一言で言うと、最初から自分の物だった、それを探し当て証明して見せた、他人に盗られるのを防いだ、という事だ。 ありとあらゆる勲功の成る手柄の木が生えて来て、そこから益が噴出するなら、人はそれをめでる。 なのに、それが木ではなく人ならば、人はそれを妬む。 ここまでが、勝つなという要求の不当性の話への追伸です。 イクオール・バット・セパレート方式の社会制度の運用実態が不公平だったからイクオール・バット・セパレート方式は間違いである、という考えは、必ずしも結果の平等を要求する考えではなく、機会の平等のみを要求する考えでも有り得る、という意味の事を私は会場で述べたが、これは、子の出生後の最も初期の段階での被教育市場への参入の自由が、イクオール・バット・セパレート方式では機会の平等の条件を満たさない(白人の子は黒人の子と競争する事なく有利なポジションを獲得でき、逆に黒人の子には白人の子に勝って有利なポジションを獲得するチャンスが与えられない)ので、イクオール・バット・セパレート方式は間違いである、という意味でだった。 この考えは論理的には、黒人の子に生まれて直ぐ白人の親に育てられる機会が与えられていないのは機会の平等に反する、という内容も含み得る、その点まで是正しろと私は主張するつもりはないし、誰が親かという事は神による不公平に含める見方も有り得るだろう。 会場で私が、いったん「機会の平等が脅かされる」という表現を使った後で別の表現に変更したのは、「脅かされる」では、脅かされたけれど保たれている、という意味に成ってしまう可能性もあるからだ。 機会の平等が成り立っていない状態に成る事を表す言葉を探して、いろいろ迷った。 --- 以下の記述は、以上の内容が以下の諸先生の発表内容への批判ではない事を示すためのものです。 以下の諸先生について、それ以上には、私に分かるはずがない。 --- 福山秀敏先生の講演は良かった。 冒頭の部分は、何だかな～、と思って聞いていたが、途中から感心させられる部分が増えた。 理科大にこういう立派な先生が居たんだな、と発見だった。 長坂教授に共通する雰囲気を持っておられる、と思った。 福山先生の発表に対する老先生の、上から下へのアプローチが上手く行かないのには深い理由がある、というコメントにも興味を持った。 そういう事情通が世の中には必要だ、と思う。 外国人＝英語という考えは偏見だ、と言っておられた外国人の人は、良く牧されている感じの善良そうな風体だった。 キリスト教徒が牧されていない人に警戒心を抱く気持ちが分かる気がした。 このページには思い残す事が多いので、後で何か気付いたら、その都度追加的に書き込む事にします。 このページの右下の最終更新日付が変化していたら、それは、私が何か書き足した、という事です。 また、書き切れなかった事は、宇田経済学や相対正義論にも書きます。
				最終更新2014年09月23日