
since 2003
イレコナビ サイトマップ
日本物理学会2009年秋季大会での私の発表は、文法物理学についての13pSH-3「円環時間を用いた新文法版シュレディンガー方程式の求解」と物理教育についての28aVE-1「解析力学理解における関数概念の重要性」の2つだった。
13pSH-3「円環時間を用いた新文法版シュレディンガー方程式の求解」は、発表会場が大して遠隔地ではなかったので、日帰りで済ませた。
旅費を安く上げるために、鉄道で特急料金の掛からない列車を乗り継いで、発表会場まで往復した。
そのため、4回も乗り継ぎしなければならなかった上、乗り継ぎ時間の短い箇所があり、その内の一箇所ででもミスすると発表予定時刻に間に合わない計算だったので、旅行は大変スリリングだった。
イボ治療のため右足の親指に血豆が出来ていたので、発表会場までの往復は大変苦痛だった。
足の血豆の事が無ければ、乗り継ぎの問題は、さして難しい問題ではなかったろう。
甲南大学に到着すると、鈴木貞吉さんが既に来ているのが見えたので、しばらくこの人と談話した。
発表会場(甲南大学岡本キャンパス5号館1階511教室)は立派な教室だったがOHPは不調だった。
近年は、液晶プロジェクターが主流に成ってから、私の発表会場のOHPは不調な事が多い。
立教大学での今年の春季大会で30pSF-8を発表した時にもOHPが不調だった。
今回もOHPの状態が良くないので、色々と位置を変えたり向きを変えたりしていると、途中で電源が入らなく成った。
それで私が困っていると、金沢喜平さんが「保護機能が働くので、一旦電源を切ると、しばらく待ってからでないと、再び電源を入れる事が出来ない」と教えてくれた。
そこで私は、しばらく待ってからスイッチを入れてみた。
すると、チャンと点いた。
しかし、電源を切るとまた電源が入らなく成るのではないか、と思ったので、念のために電源を入れっ放しにする事にした。
最初の発表者である飯田修一先生が液晶プロジェクターだったので、OHPの光がスクリーンに当たりっ放しでは具合が悪い。
それでは液晶プロジェクターの映像が霞んで見えない。
だから、私は、OHPの外部レンズの直ぐ上にメモ用紙を置いて、飯田先生の発表が終わるまではOHPの光がスクリーンに当たらない、ように工夫した。
飯田先生の発表(13pSH-1)は、発表時間と質問時間を合わせた15分を発表だけで使い切るものだったので、私も含めて誰も全く質問しなかった。
発表が終わると直ぐに飯田先生は退席なさった。
2番手(13pSH-2)は鈴木貞吉さんだった。
鈴木さんの発表は、これまでと同様に今回も、何を言っているのかさっぱり分からなかった。
私は、鈴木さんが全体としてもデタラメな事を言っている、という事を示す目的で、OHPに書かれている式の一つに分母がゼロの分数が含まれている点を指摘した。
これに対する鈴木さんの返答は「カイラルなシンメトリーですよね。シンメトリーとすると、パラメターなんですよね。このaとかbとかcはユークリッド空間を結ぶパラメターであると。ここで言うところのゼロというのは原点を持ったパラメターという意味だという事であって、だから、これをこのbに代入すればこれが不定に成るからこのものは存在しない、という事は言えないと思うんですね。だからユークリッド空間と電磁気で言う電流磁場それから力という概念のゼロの意味が違うんだと。パラメターのゼロは原点という意味であって、この式が持つところのこれは原点なんだと、そういう理解ですよねえ。それを数学でもってどういう風に表すかと言うと、ベクトルとかテンソルにしなければならん、という事ですね」というもので、私はこれを支離滅裂だと思った。
私の発表(13pSH-3)については、このページの下方に表示されているohp09au-sr-1からohp09au-sr-5までを順次提示しながら口述した。
講演概要も、このページの下方のohp09au-sr-1の直ぐ上に表示されている。
口述内容を以下に列挙する。
ohp09au-sr-2「2009年春季大会30pSF-8で見た様に、時間として実数全体を考えると、常に積分の発散に脅かされながら議論を進めなくてはいけない」の補足として、「無限大の不具合は、他に、2007年春の発表にも出て来ました」と述べた。
ohp09au-sr-2「Φ[χ]=・・・」を指して、2009年春の発表には例えばこの式が登場した、という意味の事、および、tによる-∞から∞までの積分演算の部分が発散を生じ易くする原因に成っている、という意味の事を述べた。
ohp09au-sr-2の図の説明として、この図は自由度1の系の新文法版量子論に円環時間を導入した場合について考えるための図で、これならtによる積分範囲が-∞から∞までには成らないので発散は生じない事が分かる、という意味の事を述べた。
さらに、t軸の1周の時間の長さをTとすると求解後にT→∞の極限を取れば円環的ではない普通の直線的な時間の場合の解が得られるのではないか、という意味の事を述べた。
この補足説明をさらに補足する説明として、「量子力学で用いられた周期的境界条件を思い出して下さい。あれは実際の世界が周期的だという事を主張するものではなく周期的境界条件に縛られていない実際の世界の問題を解く技術であった事を、思い出して下さい。しかし、円環時間を真に受けて実際の時間が本当に円環時間に成っている可能性を考えてみる事も、あながち無意味ではない、と思います。と言うのは、私の新文法なら時間が円環時間でも歴史が繰り返しに成らない事が可能だろうからです。」と述べた。
さらに、その理由として、私の新文法での量子歴史は既存の量子力学の量子歴史の重ね合わせだと考えられるので、一周して元に戻らないような(既存の量子力学の)量子歴史を何周も何周も無限周書いて行って、それら全ての重ね合わせを、私の新文法では(単一の量子歴史として)表現できるから、という意味の事を言った。
その際に、ohp09au-sr-2の図の赤色のグラフは量子歴史ではなく古典歴史を表している事を断った。
言葉を変えて、時間が円環ならば世界の歴史は時間がT経過したらまた同じ状態に戻ってしまうものなのか、という懸念が生じて当然だが、私の新文法を採用した場合は必ずしもそう成らない、という意味の事も言った。
ohp09au-sr-3「t=0とt=Tは同一の時刻だとする」の補足説明として、t=0もt=Tもohp09au-sr-2の図のx軸とt軸の交点だ、図に記入するのを忘れた、という意味の事を述べた。
ohp09au-sr-3では、この方程式(新文法版シュレディンガー方程式)は今までの私の発表に何度も出て来たが、χ(□-ε)の部分だけが今までと違う、x=χ(t)のグラフ(赤色の曲線)を昔の機械式腕時計のベゼルを回す様にして青色の矢印の向きにεだけ回転させてずらして得られるグラフをグラフに持つ関数がχ(□-ε)だ、という風に定義した、という意味の事を言った。
ohp09au-sr-4では、私はこのΦが新文法版シュレディンガー方程式の解である事を導き出した、というのが今回の発表の主旨だ、という意味の事を言った。
さらに、第1式は汎関数Φが汎関数aと汎関数bと関数列f0,f1,f2,・・・から如何に決まるかを表す式である事、第2式と第3式は汎関数aと汎関数bの定義でχのフーリエ展開の係数である事、第4式と第5式は関数列fに対する漸化式である事、を述べた。
ohp09au-sr-4の後半の補足説明を読んだ後で、今回の発表に直接続く様な今後の課題としては、一般解Φ[χ]=F(a0,a1,a2,・・・;b1,b2,・・・)を求める前に、Φ[χ]=F(an;bn)というタイプの特殊解を一般のnに対して求めたい、という意味の事を言った。
| 講演概要 |  13pSH-3 |
日本物理学会講演概要集 第64巻 第2号 第1分冊 17ページ。 English |
|||
| OHP |  OHP-sr-1 |
 OHP-sr-2 |
 OHP-sr-3 |
 OHP-sr-4 |
 OHP-sr-5 |
ここからは、会場での口述内容ではありません。
Φ[χ]をaとbの関数として表したかったのだが、私がちょっとやってみた限りでは初等関数を使ってシンプルに表現できなかったので、Φ[χ]をaの冪級数に展開し係数をbの関数として求めた。
この解を初等関数を使ってシンプルに表現出来た人が居たら、御一報下さい。→その後(2010年05月09日)解けました。
Φ[χ]=F(a,b)とすると、解くべき方程式は
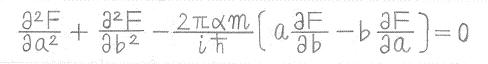
です。
ここまでは、会場での口述内容ではありません。
私のこの発表についてのご意見ご感想はwww.GrammaticalPhysics.acにお寄せ下さい。
私の次(13pSH-4)は金澤喜平さんだった。
金澤喜平さんとは、物理教育の会場では今までに何度も会ったが、素粒子論の会場で会うのは今回が初めてだった。
過去に私は物理教育の会場でこの人の発表を何回も視聴しているので、この人がどういう発表をする人なのか、今の私は大体把握している。
今回の発表も、その把握に基づく私の予想に、反しないものだった。
色々な内容が盛り込まれており、その一々が間違いであるか見る余裕は私には無かったが、おおよそにおいて、私の受けた印象は今回も悪かった。
飯田修一先生の発表に対する私の印象も鈴木貞吉さんの発表に対する私の印象も非常に悪いのだが、これらと違って金澤喜平さんの発表は、野球で言うと、私がバットを振りたく成るコースに球が飛んで来る、という状況に喩える事が出来る内容のものなので、私は、金澤喜平さんの発表に対して、飯田先生や鈴木さんの発表に対してよりも積極的に質問・コメントする。
質問時間も短いので、せめて出来る事を、と思い、「電流なんて流れてないんだ、というのは、どういう意味なんでしょう?」と質問する事から始めた。
以下に、その際の問答の内容を書いておく。
宇田:電流なんて流れてないんだ、というのは、どういう意味なんでしょう?
金澤:何で電流が流れ。電流って何ですか?
宇田:電流というのは、電荷の移動。
金澤:電荷って、プラスの電荷ですか?
宇田:マイナスもそうですが。
金澤:じゃあ逆ですね。
宇田:どういう事ですか?
金澤:電流の向きじゃないですね。
宇田:うん、ああ、そもそもだから向きが
金澤:電流じゃないですね、それは。
宇田:いや、あの、
金澤:流れるのは電子でしょ?
宇田:電流が流れているとは電荷が移動している事である、まあこれが電流の定義だと思うんですが、まあ、あるいは電流が流れているという文章の定義だと。
金澤:向きが違うでしょ?
宇田:向きが違う、
金澤:電流の向きには電荷は流れていませんよね?
宇田:はあはあはあ、それは、あの、
金澤:逆向きですね、電子なら。
宇田:いや、電流が流れている流れていない、という事に加えて、その量は幾ら幾らである、向きは幾ら幾らである、という文章を作って、それの定義を言った所まで行くと、それは問題無いんじゃないでしょうか?
金澤:自然現象としては、技術的には重要な概念ですけれど、物理の本質を捉えようとする場合に、電流というのは流れていないんです。見ているのは、測っているのは磁場です。
宇田:電流の向きと電荷の移動の向きが違う場合がある、というのは、単なる規約の問題だと思いますよ。
金澤:電荷も流れていない。
ここまでが、問答の内容です。
ここからは、帰宅後に考えた事です。
会場では私は、金澤さんは相変わらず無茶な事を言ってる(特に最後の「電荷も流れていない」という発言は傑作だ)なあ、と思ったのだが、家に帰った後で金澤さんの言わんとする事が私にも分かった。
そして私は彼の発言を、言っている事は間違いだが言おうとしている事には正しい部分もある、と評価するのが正しい、と思う様に成った。
「電流が流れる」という文から「流れる」だけを切り離して、「流れる」という語に常識的な意味付けを行ない、その意味付けを非常に尊重するならば、電流は流れていないんだ、という事が、彼の言わんとする事だった、と思われる。
それなら、それは、正しいし物理教育においては意味がある。
しかし、その事を「電流なんて流れていない」という言葉で表現するのは間違っている。
また、教育領域ではなく研究領域においては、その主張には価値が無い。
物理教育においては、次のような意味があると思う。
(E-1)電子を学ぶ事による電流イメージの変化を生徒に意識させる。
(E-2)「電流」=「電気の流れ」という語句の様に、それを構成する要素語の意味から意味が導き出されるのではない語句や文、というものが理科には有る事を生徒に教える。
(E-3)中学1年生の数学で登場する負の数についての生徒の理解を深める。
「電流が流れる」という言い方は、普通用いられるので、それでも良いが、ここでは正確な分析のために、「電流が流れる」では「電気の流れが流れる」という風に成ってしまい「流れ」の部分が重複して不合理なので、金澤さんの批判は「電流は(電気の)流れである」という認識に対する批判だ、という風に、修正して論じる事にする。
その批判の内容を私流に言い直すと「流れという言葉を常識的な意味で用いるならば、電流は電気の流れではなく電気の流れの数え方である(電荷の移動の数え方である)」という表現に成る。
もちろんこれを「電流なんて流れていない」という言葉で表現するのは間違っているが、金澤さんのこの批判は正しいし、教育現場で生徒にこれを意識させる事は(E-1)の実践として非常に優れた方法だ、と私は思う。
教科書の記述に反映させた方が良いかもしれない。
この事に気付いた時に私は、金澤さんは実は誠実な人なのではないか、と思う様に成った。
他人に理解されずに、さぞかし辛い思いをした事だろう。
上で私が、「言っている事は間違いだが言おうとしている事は正しい」と書かずに「言っている事は間違いだが言おうとしている事には正しい部分もある」と書いたのは、金澤さんには(E-2)の視点が欠けているからだ。
研究の観点から言うと、「電気の流れなんて直接測定出来ない。測っているのは磁場だから、電流なんて無い」という主張は、エルンスト・マッハ流の実証主義に属するだろう。
実証主義を独自に考え出したとしたら、それは才能としては立派な才能だと思う。
しかし、随分と昔に既に出ている考え方なので、その考えを発表する事は研究としては業績には成らず、研究領域でそれを発表する事に価値は無い。
今回の金澤さんの発表は「電流なんて流れていない、だから・・・を提案する」という内容だから、「電流なんて流れていない」の部分は、正しくさえあれば、無価値でも、その事(無価値である事)は、提案内容を無価値だとする理由には成らないが。
既に出ている、という事は、独自に考え出した事を証明出来ない、という事でもある。
また、磁場だって直接測定出来ず、磁場中の電流に働く力を測定する事によって間接的に磁場を測定する等するわけだから、電流よりも磁場の方がプライオリティが高いわけでもない。
コンデンサの極板に流れ込む電流は磁場を測定しなくても極板間電圧の時間変化を測定する事によってでも測定できる事なども、反論として挙げる事が出来るだろう。
だから、金澤さんの電流概念に対する批判は徹底していないのであって、その分、実証主義の実行を意図的に途中で止めているのではないか、という疑念を私は持つ。
そうだとすれば、それは不誠実な態度だ。
自分仮説・俺仮説で良いなら、そんなもん幾らでも出してやるよ、という考えの人が居ると思うが、キチンと誠実さを貫くならば自分チェック・俺チェックというものは結構厳しいのであって、正直に、これは根本的に新しくて正しい、と思えるようなアイデアなんて、そう易々と出せるものではない。
実証主義の実行を徹底しようとすれば、電流だけでなく、あらゆる物理量が、そんなもの便宜に過ぎない、という事に成ってしまうはずだ。
それはそれで一概に間違いだとは言えない考え方なのだが、実証主義を物理学研究のココ掘れワンワンとして見る時には、掘っても何も出て来なかった、あるいは、相対性理論や量子力学が実証主義の産物だという見方を取るとしても既に堀り終わっている、というのが史実の教える所だろう。
西暦2009年の今そんな所を掘るのは時代錯誤なのだ。
では、どう考えれば良いかと言うと、どこまで行っても徹頭徹尾好都合な便宜は物理的実体である、という風に考えれば良い。
個別の物理学者の事はいざ知らず、物理学全体について言うと、実証主義の洗礼を受ける事によって物理学はこの哲理を獲得した、と言えよう。
この様な実証主義とその超克の理屈(幾分私の独断に偏っているかもしれない)は、教育的にも価値があると私は思うが、電子を初めて学んだ時点でこれを見せるのは早過ぎるだろう。
大学相当の物理学の勉強に入ってから、それと並行して教養として学ぶぐらいが丁度良いと思う。
中学・高校相当の勉強では、まず理科や物理に対するゆるぎない信頼感を醸成し、批判的考察はその上に立ってでなくてはいけない、と私は思う。
電流という数え方のどこまで行っても徹頭徹尾好都合な様子を見る事は、E-3の実践としても極めて有効である。
たとえば、隣接する2つの立方体を考え、一方をAとし他方をBとする。
最初Aの中に電荷-eの電子が1個だけ入っており、Bには何も入っていなかったとする。
さらに、その後、その電子がA内からB内へと移動したとする。
すると、電子のその移動によって、A内の電荷は-eから0へ、B内の電荷は0から-eへと、変化した事になる。
つまり、B内の電荷がe減ってA内の電荷がe増えた事に成る。
これは、電荷がeだけBからAに移動した、という事で、その移動の向きは電流の向きに一致している。
こう考えると、電子の移動の向きが電流の向きと異なるから電流は流れではない、とは言えなくなるはずだ。
この様な負の数の持ち味に起因する驚異的な好都合は、他にも色々と考えられるだろうから、理科の先生には自分で考えて欲しい。
28aVE-1「解析力学理解における関数概念の重要性」の発表については、物理教育の会場まで高速バスを福山→博多→熊本という風に乗り継いで行った。
参考:博多駅交通センターで撮った写真, 熊本交通センターホテルで撮った写真
以下、熊本の会場(熊本大学黒髪キャンパス文学部・法学部1階B2教室)での事について書く。
私の発表(28aVE-1)については、このページの下方に表示されているohp09au-13-1からohp09au-13-7までを順次提示しながら口述した。
口述内容は、おおよそ講演概要のそのままの読み上げだったが、若干補足説明もした。
以下にその内容を列挙する。
ohp09au-13-3の右下の図を使って、大抵の先生がするであろう、1組のq, dq/dt, tだけなら独立に選べるよ、という説明の内容を図解した。
さらに「ここにはいかにも学生の疑問が整然としたものであるかの様に書かれていますが、無理に言葉で簡潔に説明しようとしたらそう成った、という事であって、学生時代の私の頭の中はもっと混沌としたものでした。今思い出すのは、何度考えても、qもdq/dtもtの関数でLがqとdq/dtとtの関数なんだから結局Lもtの関数なんでしょ、という所に戻って来てしまったのを思い出します」と述べて、ohp09au-13-3の蛇行した図は、qもdq/dtもtの関数でLがqとdq/dtとtの関数なんだから結局Lもtの関数なんでしょ、という考えのイメージ図である事を、述べた。
ohp09au-13-3「qとdq/dtとtが独立だからラグランジュ方程式が成り立つ、のでもない」とはどういう事かohp09au-13-4に書かれている、という意味の事を言った。
ohp09au-13-4では、講演概要のミス(zと書くべき所に誤ってtと書いている事)を訂正した。
ohp09au-13-5では「ここで私は、先生は学生の質問には何でも答えられなくてはいけない、と言っているのではありません。自分がチョッと分かったからといってね、分からなかった人のを何で分からないんだと言うのは、それは褒められた態度じゃないです。分からない事はあって当然だと思います。だが、解決していない状態を解決しているかの様に言いくるめる態度は微塵もあってはいけない。先生にもまだ分からないがこれは肝心な事だから考え続けなさい、とアドヴァイスする判断も大切です。ただし、私が学生時代に解析力学の先生から言いくるめられた、という事はありません。無用の過ぎた理屈という意味の事を言われたのは量子力学について別の先生からです。」と述べた。
ohp09au-13-2「既成の理論を超えた新しい事」やohp09au-13-5「基礎理論に関して根本的に新しい事」の具体的可能性をohp09au-13-6で提示した。
第4式はFをqとdq/dtの関数と考える思考枠組みを超えた根本的に新しい事だ、という事を、Fのqやdq/dtによる偏微分を使って第4式と同じ事を表す事は出来ない、無理に書こうとすると第5式に成るが、第5式は第4式と等価ではない、という点を指摘する事によって説明した。
その後、言い忘れた事として、ohp09au-13-2「yはxの関数であるという風に使うタイプの理解をしていたのでは解析力学を正しく理解できない」という部分について「この事で私の学習は約1年ぐらい遅れたのではないかと思います」と述べた。
| 講演概要 |  28aVE-1 |
日本物理学会講演概要集 第64巻 第2号 第2分冊 314ページ。 |
|||||
| OHP |  OHP-13-1 |
 OHP-13-2 |
 OHP-13-3 |
 OHP-13-4 |
 OHP-13-5 |
 OHP-13-6 |
 OHP-13-7 |
質疑応答時間には、まずは誰も質問しなかったので、座長の並木雅俊先生に促されて、qもdq/dtもtの関数でLがqとdq/dtとtの関数なんだから結局Lもtの関数なんでしょ、という考えについて「この疑問は、Lがどういう関数なのかはLがtのどういう関数であるかに尽きる、だったらqで偏微分もq-dotで偏微分も無いじゃないか、という疑問(その頃そういう表現は思い付かなかったと思いますが、あえて言葉で言うなら、何かそんな感じのもの)ですね」という補足的コメントを行なった。
並木先生から、何を皆さんにお伝えしたいのですか?という意味の質問が出たので、これに対して私は「要するに、解析力学の従来の教授法の中に付加的にそういう補足説明を入れるべきである、という事ですね」と答えた。
続いて並木先生から「単なる3変数で考えちゃ何故いけないんですか?qとq-dotとtは別個の独立変数だと考えて何も問題無いじゃないですか?」という質問が出たので、これに対して私は、あれ?言ったはずなのになあ、と思い、その気持ちを「3変数ですけど」という言葉にした後で、ohp09au-13-3の該当箇所を指し示しながら「qもq-dotもtの関数だし、qとq-dotはq-dot=dq/dtという関係で結ばれているので、これらは独立ではないのではないか、という疑問を持ってしまう」と答えた。
すると並木先生が、そのように思った学生のためにコメントをしたという事ですね、という意味の事を言ったので、私は良く考えながら「そうですね」と答えた。
その後、別の参加者( 日本物理学会2008年秋季大会で出会った応用物理学会の人 )から、学習時期について、大学1年生の前期で習う内容についてですね?という意味の質問が出て、これに対して私が、解析力学は大学2年生ぐらいのはずです、まず常微分方程式の初等力学を学んで、その後で解析力学を学ぶ様に成っています、という意味の事を言って、私の発表は終わった。
ここからは、帰宅後に考えた説明です。
発表時には思い付かなかったが、帰宅後、Lもtの関数なんでしょ、という理解の状態を伝えるには、Lを物理量だと思っていた、という風に表現すれば分かり易い、という事に気付いた。
「あれ?言ったはずなのになあ」の部分について、並木先生がなぜ疑問に思ったのか想像してみるに、善意に解釈するならば、私が批判する「‘関数’という語を“yはxの関数である”という風に使うタイプの理解」というものを、1変数関数で考えるタイプの理解だ、という風に並木先生は勘違いなさったのかもしれない。
そして、Lもtの関数なんでしょ、という考えがこれに当たり、1変数関数ではなく3変数関数を考えれば良い、という風に並木先生は思ったのではないか。
しかし、私が言っているのは、関数と関数の値を混同する考えへの批判(これ自体は私以前から数学基礎(数学初歩ではない)の常識として存在するが、物理学の学習においてこの批判が最も必要とされるのは解析力学の学習という局面である事を指摘したのは私が初めてだと思う)であって、「‘関数’という語を“yはxの関数である”という風に使うタイプの理解」とは、何変数関数であるかに関わらず、関数と関数の値を混同する考えの事だ。
「‘関数’という語を“wはxとyとzの3変数関数である”という風に使うタイプの理解」は、関数と関数の値を混同する考えだから、「‘関数’という語を“yはxの関数である”という風に使うタイプの理解」に当たる。
その意味で、Lはqとq-dotとtの関数だ、という見方は、ラグランジアンとラグランジアンの値を混同しているので、「‘関数’という語を“yはxの関数である”という風に使うタイプの理解」に当たる。
Lもtの関数なんでしょ、という疑問は、Lはqとq-dotとtの関数だ、と考えなかったから生じたものではなく、Lはqとq-dotとtの関数だ、と考えたから生じた疑問なのだ。
私の「3変数ですけど」という発言は、この事情と並木先生の質問内容の不調和をいぶかってのものだった。
私の「そうですね」という発言について、良く考えながらの返答だっにもかかわらず、後で考えてみると、最善の返答ではなかった。
と言うのは、講演概要にも書いてあり発表でも私が読み上げた通り、今回の私の発表はそうでない学生(私と同じ疑問を持った学生以外の学生)のためでもあったからだ。
ここまでは、帰宅後に考えた説明です。
参考:解析力学正典
28aVE-2「イラストを用いた物理学の紹介」の質疑応答時間に、発表内容のイラストに何か新しい切り口は含まれているか?という意味の質問などが出た。
また、並木先生から若干のコメントがあった。
それらを聞いて私は発表者に向かって「新しい切り口でなくても、今までイラスト化されてなかったものまで何でもかんでもイラスト化する、というのには意味がありますよね」とコメントした。
また、並木先生のコメントに、あまり自分の履歴にこだわらずに自由にやった方が良い、という意味の言葉が含まれていたので、私は、この発表で紹介された活動においては発表者の東大で博士号を取ったという自意識が適切に使用されておりその自意識のために活動が不自由に成っている事は無い、と思ったが発言はしなかった。
28aVE-11「第5回全国物理コンテスト・物理チャレンジ2009報告IV.全体報告」の質疑応答時間に発表者(並木先生)に日本物理学会2009年春季大会28aYE-4「物理チャレンジ・オリンピックの報告を見ての感想」(私による発表)の存在を紹介した。
それに加えて、私のその発表の内容の雰囲気を伝えるために、「思ったのですが、理論問題よりも実験問題の方が中心という事であれば、いっその事もう理論問題は筆記試験とかいう名前に変えてしまうとかしたら良いのではないか、とか、理論問題に関して発展的な問題というと何故相対性理論だとか、大学の内容ばかり出すんだろう、その辺りに私は発想の貧困というものを感じてですねえ、高校物理にももっともっと味わえば何かその発展的な問題、今まで人が気が付かなっかった問題というものを見出す事ができるか、それが非常に困難であるから、それだけに、その、不可能に近いような事が出来た生徒をその部分で表彰してあげる事が良いんではないか」とコメントした。
このコメントに対して並木先生は、「私たちは別に相対論を載っけたから量子論を載せたから発展だとは思ってません。基本的には良く考えなきゃあ出来ない、思考をもうちょっと使う、それを発展と考えてます。ですから思考法に使うのがたまたま相対論が出て来たというだけの話で、もちろん他の問題でも電磁気学の問題でも基本的な力学の問題でも、・・・に考える、先ほどの波の問題・・・でしたら、当然これを我々は発展的な問題と考えておりますので、ご理解を頂きたいと思うわけでございます。(・・・部分は良く聞き取れない)」と釈明なさった。
ここからは、帰宅後に考えた説明です。
日本物理学会2009年春季大会28aYE-4「物理チャレンジ・オリンピックの報告を見ての感想」(私による発表)を見れば分かるが、私の批判は、相対論や量子論という特定の科目の出題にのみに向けられたものではなく、問題に「もうちょっと思考を使う」という特性を付与する事が、もうちょっと予備知識を使う、つまり上の学年の問題を出す事ばかりによって達成されている、という事全体に向けられている。
だから、電磁気の問題でも力学の問題でも、その問題を普通の高校物理の問題よりももうちょっと思考を使う発展的な問題にするために、大学の電磁気学の問題や大学の力学の問題を出題するならば、その行為にも、私の「それは発想の貧困だ」という批判は向けられており、実際、物理チャレンジや物理オリンピックの問題は、高校生に大学の物理を出題する事によって高校生にもうちょっと思考を使わせようとするもの、に成っている。
上の学年で習う事を教えられずして自力で考え出す種類の才能を調べる問題が、試験問題に最も重視される部分として含まれているべきだ、というのが私の考えである。
そのためには、相対論や量子論その他上の学年で習う事(あるいはそれらの基本的な考え方)を予備知識として与えて、その土俵の上で競争させても、無駄である。
相対論を教えられて分かる能力と、相対論の無い時代に相対論を考え出す才能とは、別だからだ。
ここまでは、帰宅後に考えた説明です。