
since 2003
イレコナビ サイトマップ
日本物理学会2012年秋季大会での私の発表は、文法物理学についての12aST-2「作用汎関数を解に持つ新文法版シュレディンガー方程式」と、マクロ経済学についての18aFG-2「仕分け論理と学界の社会的地位」の2つだった。
12aST-2の発表会場へは福山駅から夜行高速バスで行った。
京都駅に到着した直後の記念写真が私の写メール投稿ブログ「即達」の2012年09月12日の記事に掲載されています。
12aST-2の発表会場は、京都産業大学12号館4階12402教室の予定だったが、大会本部によって、6号館3階516教室に、急きょ変更された。

私の写メール投稿ブログ「即達」の2012年09月12日の別の記事にも、同様の写真が掲載されています。
18aFG-2の発表会場へは、夜行高速バスドリームスリーパー号で行った。
夜行高速バスで広島県から関東まで行く場合には、この様な贅沢な車両でないと、体力的に無理がある事を、これまでの旅行経験から学んだ。
贅沢と言っても、それは、バスにしては、であって、新幹線と同程度の運賃だし、宿泊無しだから、昼間に新幹線で行くよりは安く上がる。
単位時間当たりの居心地は新幹線よりもずっと上、乗車時間が新幹線の2倍以上、両方合わせて、到着までの疲労は新幹線と同じぐらいだった。
私の写メール投稿ブログ「即達」の2012年09月18日の記事に、車内での様子を撮った写真が掲載されています。
横浜駅到着時の様子も、同じ日の別の記事に掲載されています。
18aFG-2の発表会場は、横浜国立大学経済・経営学部講義棟1号館1階107教室だった。
12aST-2では私は、OHPを掲示しながら、次の様に口述した。
| 発言タイミング | 発言内容 | 注釈 |
| ohp12au-sr-1 | 今回の発表内容の詳しくは、このwww.GrammaticalPhysics.acというウェブ・サイトの、Forumという所の中の、Problems in Grammatical Physicsの中の、更にWhat in the World is an Action Functional?の中の、更にTo Interpret the Integrand of Feynman's Path Integral as a Solutionという所に、書いております。 | 該当記事へのリンク |
| ohp12au-sr-2 | それでですねえ、新文法版シュレディンガー方程式というのは、(ohp12au-sr-2の前半の式を指して)これなんですが、これは、日本物理学会の2007年の春の大会の28pSL-11で、私が発表しました。 その時発表したものと、(ohp12au-sr-2の前半の式の右辺のV[χ]を指して)ここの部分が少し違います。 最初に2007年に発表したものでは、ここが、関数χの時刻tにおける値の関数をtで積分したもの、という風に書いておりますが、今日の発表においては、それをもう少しちょっと一般化したもの、という事で、関数χの汎関数の値という風に、ここは成っておりまして、最初に発表したものよりも少し譲歩した形に成っている、という事です。 この新文法版シュレディンガー方程式は何かと言いますと、これは、汎関数Φというものに対する方程式です。 で、ちょっと、まあ、だから、(ohp12au-sr-2の前半の式のΦ[χ]のχを指して)この引数の所が関数という事ですね。 χが関数という事です。 で、(ohp12au-sr-2の前半の式の左辺のχ(□-ε)を指して)これは何かと言いますと、この□-εなる記号を私は作って使っておりますが、これは、関数χのグラフを水平軸の右の方向に、まあt軸のプラスの方向にですかね、εだけ平行したグラフをグラフに持つ様な関数というものを、このχ(□-ε)というので書いております。 で、この新文法版シュレディンガー方程式が、(ohp12au-sr-2の後半の式を指して)下に書いておりますこれ、は何かと言いますと、ファインマンの経路積分の被積分汎関数ですね、ファインマンの経路積分の被積分汎関数を解に持つ様に、新文法版シュレディンガー方程式がそれを解に持つ様に、(ohp12au-sr-2の前半の式の右辺のV[χ]を指して)このポテンシャルの部分を決める、という事を、今日発表します。 それで、何をやるかと言いますと、ファインマンの経路積分の被積分汎関数に、と言うのは、(ohp12au-sr-2の後半の式を指して)これt軸の方向に平行移動しても値が変わりませんから、(ohp12au-sr-2の前半の式を指して)こっちのこの新文法版シュレディンガー方程式に代入した時には、左辺はゼロです。 (ohp12au-sr-2の前半の式の右辺を指して)だから右辺を、この、第1項と第2項に分けて、第2項を計算して、前に出て来た部分がポテンシャルに。 チョッと符号が変わりますが、その様な計算をするだけで良い、という事なんですが。 |
「関数χの時刻tにおける値の関数をtで積分したもの」とは、V(χ(t))の事です。 日本物理学会2007年春季大会報告記事 「平行した」は「平行移動した」の言い間違いです。 「で、この新文法版シュレディンガー方程式が・・・今日発表します」の部分が分かり難いですが、この部分は「で、この新文法版シュレディンガー方程式が、下に書いておりますファインマンの経路積分の被積分汎関数、を解に持つ様に、このポテンシャルの部分を決める、という事を、今日発表します」という意味です。 「それで、何をやるかと言いますと、・・・その様な計算をするだけで良い、という事なんですが」の部分も分かり難いですが、この部分は「それで、何をやるかと言いますと、ファインマンの経路積分の被積分汎関数を、新文法版シュレディンガー方程式に代入し、右辺を、第1項と第2項に分けて、第2項を計算して、前に出て来た部分の符号を変えたものをポテンシャルとする、という事をやります。その様な計算をするだけでよい、という事なんです。と言うのは、ファインマンの経路積分の被積分汎関数の値はχをt軸の方向に平行移動しても値が変わりませんから、新文法版シュレディンガー方程式に代入した時には、左辺はゼロに成るからです」という意味です。 ハンドルの切り直しによって、分かり難く成っています。 |
| ohp12au-sr-3 | それを書きますと、まあ、(ohp12au-sr-3の冒頭の式を指して)こういう計算をすれば良いでしょうという事なんですね。 (ohp12au-sr-3の冒頭の式の左辺のΦを指して)ここのΦの所には、ファインマンの経路積分の被積分汎関数を代入して、で、(ohp12au-sr-3の冒頭の式の左辺を指して)これを計算して、(ohp12au-sr-3の冒頭の式の右辺を指して)こういう形のものを出して、で、(ohp12au-sr-3の冒頭の式の右辺のV[χ]を指して)ここのVの部分を抽出すれば、求めるポテンシャルの部分が求まったという事なわけです。 欲しいポテンシャルの形が求まったという事に成るだろう、という事で、(ohp12au-sr-3の第2式を指して)結局この部分の計算だなあ、したいのは。 |
- |
| ohp12au-sr-4 | (ohp12au-sr-4の中段の矢印の右の式を指して)これをですね、まず、このファインマンの経路積分の被積分汎関数を、まず、いきなり、(ohp12au-sr-4の中段の矢印の右の式中の積分を指して)この作用汎関数で書かずにですねえ、(ohp12au-sr-4の中段の1行目の式を指して)この様に書いておきます。 まず、Φ[χ]をD(t1-t2)を使って、この様に表しておけば、D(t1-t2)を(ohp12au-sr-4の上段の矢印の右の式を指して)この様なものに近付ける極限を取った時に、Φ[χ]はファインマンの経路積分の被積分汎関数に近付きます、という事ですね。 そうして、その時にですねえ、極限を取る前の形で(ohp12au-sr-4の下段の1行目の式を指して)これを計算します。 この計算をしなければいけないなあ、というのが一つ前のOHPで提示した問題ですが、(ohp12au-sr-4の下段の等号の右の式を指して)これは極限を取る前の形で計算して、その後でこの極限を取ると、(ohp12au-sr-4の下段の矢印の右の式を指して)こういう風に成りました、という事で。 で、Φの前に(ohp12au-sr-4の下段の矢印の右の式中のΦの左の部分を指して)こう何か飛び出してるので、ここの符号を変えたものがVですね、求まりましたね、という事です。 ここでですね、ちょっと一つ断り書きが有ります。 講演概要はですねえ、講演概要には、(ohp12au-sr-4の下段の矢印の右のD(0)を指して)ここのD(0)に対する注釈としては、D(0)というのは(ohp12au-sr-4の上段のt1-t2を指して)ここのt1-t2の所にゼロを代入したDの値という事なんですが、 |
- |
| ohp12au-sr-6 | これに対する注釈として、講演概要には、(ohp12au-sr-6の第1式を指して)この様に書きましたが、まあ、どうせ発散する量だからどっちでも良い、みたいなニュアンスもありますけど、これはちょっと良くないなあ、と思いまして、(ohp12au-sr-6の第2式を指して)この2番目に書いた、この方が良い。 つまり、デルタ関数の引数をゼロに近付ける極限、という風に考えるよりは、先に引数をゼロに置いておいて、関数をデルタ関数に近付ける極限、という風に考えた方が良いかな。 どちらにせよ、これ発散してしまうので、その点が今回の発表の難点。 Vは求まりました、ただしD(0)は発散します、というよりは、まあ、そういう言い方も出来るけれど、厳密主義的に言うと、だからVは存在しません、という結果が出て来たという、そういう面もあります。 |
- |
| ohp12au-sr-5 | でまあ結論としては、さっきの飛び出した部分がVという事で、ここ書きますと、(ohp12au-sr-5を掲示して)こう成ります。 (ohp12au-sr-5の2番目の等号の右の式を指して)これ2番目はただちょっと整理しただけです。 で今回この時間としてですねえ、円環時間というものを採用しております。 円環時間というのは、(ohp12au-sr-5の式中の積分記号を指して)この積分の上端に書いておりますTというこのTを一周の長さに持って、Tだけ進むと元に戻ってしまう様な、輪につないだ時間軸を考えております。 で、これはですねえ、日本物理学会の2009年の秋の大会の13pSH-3で私が持ち出しました。 |
日本物理学会2009年秋季大会報告記事 |
画像をクリックすると拡大表示されます。
| 講演概要 |  12aST-2 |
日本物理学会講演概要集・第67巻・第2号・第1分冊・6ページより。 | ||||
| OHP |  OHP-sr-1 |
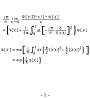 OHP-sr-2 |
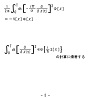 OHP-sr-3 |
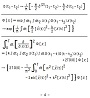 OHP-sr-4 |
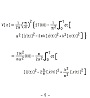 OHP-sr-5 |
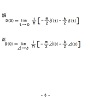 OHP-sr-6 |
質疑応答時間には、鈴木貞吉さんと私の間で、次の様な問答が行われた。
| 発言者 | 発言内容 | 注釈 |
| 鈴木 | 私の意見なんですけどね、 | - |
| 宇田 | はい。 | - |
| 鈴木 | 結局そのt1とt2を求めなければ、 | - |
| 宇田 | うん。 | - |
| 鈴木 | 意味が無いと思うんですよね、 | - |
| 宇田 | えーと、あの~、 | - |
| 鈴木 | 理論にね。 | ここまでの鈴木さんの発言をつなげると「私の意見なんですけどね、結局そのt1とt2を求めなければ、意味が無いと思うんですよね、理論にね」と成る。 |
| 宇田 | はあはあ、それは幾らでもあるんですけど。 t1とt2は積分変数なので、最後の結論には出て来ないんです。 t1とt2は求めるものではなくてね、t1,t2というのは、 |
「幾らでもある」というのは、意味なら幾らでも有る、という意味です。 |
| 鈴木 | 結局いつの間にか消えてしまってるわけですよね。 | - |
| 宇田 | そうですねえ、はい。 | - |
| 鈴木 | だけど、それではねえ、 | 過去に宇田が鈴木から、新文法版量子力学は何の役に立つのか訊かれて、コンピュータの新しい動作原理を与えるかもしれない、と答えた事を受けての発言だと思われる。 |
| 宇田 | うん。 | - |
| 鈴木 | コンピューターの原理には使えないと思うんですよね。 | ここまでの鈴木さんの発言をつなげると「結局いつの間にか消えてしまってるわけですよね。だけど、それではねえ、コンピューターの原理には使えないと思うんですよね」と成る。 |
| 宇田 | コンピューターの原理には使うつもりはないです。 | ここで宇田は、自分が、コンピュータの新しい動作原理を与えるかもしれない、と答えた事、を忘れているために、それに反する事を言ってしまっている。 |
| 鈴木 | う~ん。 t1とt2が求まれば、コンピュータの原理に成る様な気がするんですけどね。 それが、まあ結局いつの間にか消えてしまってると、いう事は、この理論は何ら意味が無いと、私は思うんですけど。 |
t1とt2が求まればコンピュータの原理に成る、という事はありません。 |
| 宇田 | そうですか? t1とt2というのは、これ、まあ例えば(ohp12au-sr-4の冒頭の式の左辺のt1-t2を指して)ここだったら、t1,t2という文字を使わなくてもいいですけど、ここは、例えばt1-t2の所をτと書いて、(ohp12au-sr-4の冒頭の式の右辺のt1-t2を指して)ここもτと書いて、要するにDという関数の形を、どういう所に近付けて行くか、どういう極限を取るか、Dという関数をどういう風に変形させて行くか、という事を表しているのがこの式だから、ここでは、まずt1,t2という文字を使う必要があるわけですねえ。 だから例えば、ここを基点にして考えれば、t1,t2が消えてしまった、途中で消えてしまったという問題自体が、存在しません。 それから(ohp12au-sr-4の2番目の式を指して)この2番目ですねえ、2番目はこれは、t1,t2というのはこれは積分変数ですから求めるものではない、という考え方に成ります。 この2番目のt1,t2というのを積分変数として用いた(ohp12au-sr-4の2番目の式の右辺を指して)この積分を書くために、これ1番目の式を(ohp12au-sr-4の冒頭の式を指して)こういう風に考えたわけだから、t1,t2というのは求めるものではない、という事が分かると思います。 |
前半については、t1,t2が ∀t1,t2;D(t1-t2)=・・・ という形で現れているのでダミー変数である、という観点を、後半については、t1,t2が積分変数として現れているのでダミー変数である、という観点を、提示しています。 |
| 鈴木 | よく分からないですねえ。 新文法の意味がですねぇ、どうも良く分からないです。 |
- |
| 宇田 | 新文法は2005年の秋の大会で発表した時に、新文法という言葉は初めて私は使ったと思いますが、たとえば、その講演概要であるとか、報告記事もありますので、その辺りを参照して下さると、何か手掛かりがつかめるかもしれません。 | 日本物理学会2005年秋季大会報告記事 |
| 鈴木 | そういう機会がありましたらね、読みたいとは思うんですけども、なかなかそういう機会が無いんで。 | - |
この問答の後で私は、次の様に補足コメントした。
| 発言内容 | 注釈 |
| 今回はこれ結局、以前作用汎関数を解に持つ新文法版シュレディンガー方程式を作りたいなあと思った時に出来なかったのが、まあ最近では出来る様に成った、やってみると出来た、というのは、気付きがあって、やってみると出来ました、という意味ではちょっと進歩があったのですが、でそれで何が分かったのか、という事については、どちらかと言うと何も分からなかった、作用汎関数を解に持つ新文法版シュレディンガー方程式という文脈というもの自体が、あまり見込みが無いものかなあ、という事をむしろ思う様に成りました。 青森で発表したこれ何年だったかなあ、どの季節だったかちょっとよく思い出せませんが、青森で発表した時には、作用汎関数が新文法版シュレディンガー方程式のポテンシャルに成っているという、そういうものを発表しましたが、どちらかと言うとですねえ、そちらはなんか当たってるなあ、という気がしたんですが、こちらの作用汎関数を解に持つというのは、これは、なんか、まあ将来的に何かにつながればいいなあ、という期待はするんですが、ちょっと現段階では、どちらかというと見込み薄 |
最後に「見込み薄です」と言い切らずに「見込み薄」で止めたのは、時間切れを知らせるブザーが鳴ったためで、ルール遵守を誇張して表現するギャグです。 |
文法主義についての私の発表についてのご意見ご感想はwww.GrammaticalPhysics.acまたはWooder!掲示板にお寄せ下さい。
18aFG-2では、まず最初に、座長と私の間で、次の様な対話があった。
| 発言者 | 発言内容 | 注釈 |
| 座長 | 2つ目の講演は、仕分け論理と学会の社会的地位というタイトルで、宇田英才教室の宇田雄一さんに、御講演いただきます。 じゃあ、よろしくお願い致します。 |
発表内容から、所属を物理学正典ではなく宇田英才教室として講演申し込みをした事を、帰宅後に思い出した。 OHPには物理学正典と書いてしまった。 |
| 宇田 | よろしくお願いします。 物理学正典の宇田雄一と届けてたんじゃないか、と思いますが、あれ?宇田英才教室に成ってますか? |
|
| 座長 | 宇田英才教室に成ってます。 | |
| 宇田 | あ、そうですか、はい。 |
| 発言タイミング | 発言内容 | 注釈 |
| ohp12au-13-1 | 仕分け論理と学会の社会的地位というタイトルで発表します。 発表と言っても研究成果といったほどの物ではなくて、自分の考えを述べる、といった感じのものなんですが。 民主党政権によって2009年の11月に行われた仕分けの話なんですが、それについての話で、まあ純粋な学理の追求といった様なものに対する批判というものが、強くそこに打ち出されていてですねえ、純粋な学理の追求をしている側の人からはあまり有効な反論がなされていなかったなあ、と思いました。 特に、何故そのような研究をする必要があるのか、という様な事に対するですねえ、あまり有効な反論を聞かないので、私はこの様に反論したらいいのではないかと思う事をちょっと、発表します。 |
- |
| ohp12au-13-2 | 社会をですねえ、人間の人体に例えた時に、学問の世界、学界というのは、人体の中の脳の中の大脳の中の大脳新皮質の中の、まあ何か特定の領域に対応するだろう、と思います。 で、まあ学界の中の個々の学者というのは、脳の特定の領域の中の神経細胞に相当するだろうと。 で、人体における血流というのが社会における資金流の様なものに対応するんではないかと、この様に考えました。 大脳新皮質というのは、この、何故必要なのかというのが必ずしも明確ではないので、かと言って必要である事は明らかであるけど。 それとの対応において、純粋な学理の追求というものも必要だ、という事は明らかであろう、という、そういう考えなんですが、それで具体的な、ちょっと、事を調べてみまして、私もその、脳だとか人体だとかいう事に関しては素人なんで、Wikipediaとか、ちょっと調べてみました。 こんな事が出て来ました。 |
- |
| ohp12au-13-3 | 脳の血液の循環量は心拍出量の15パーセント、酸素の消費量は全身の20パーセント、グルコース(ブドウ糖)の消費量は全身の25パーセント。 さらにですねえ、脳の質量というのがですねえ、これは全身の質量の2パーセント程度だそうです。 で、脳の神経細胞の個数は、これは0.2パーセントぐらいの様ですね。 あ、ごめんなさい、あぁ、これは自分で計算したのか。 脳の細胞の個数は(ohp12au-13-3の表中の3000億個という部分を指して)このぐらいだ、と書いてありました。 人体の細胞の個数は(ohp12au-13-3の表中の60兆個という部分を指して)このぐらいだ、と書いてありました。 よって、まあ脳の細胞の個数というのは、これは人体の0.5パーセント程度かなあと、その様に思いました。 あ、それからあと、脳全体に比して脳の神経細胞というのは、大体1割程度なんだそうです。 これ個数にしてなのか質量にしてなのか、よく分からないので、まあ大雑把に、両方とも0.1を掛けておきましたが。 そうすると、人体全体に比べて、脳の神経細胞というのは、まあ個数にして0.05パーセント、質量にして0.2パーセント程度という事に成ります。 で、まあ社会の問題を考えるのに分かり易くするために、パーセントではなくて「1億分の」で考えてみると、まあ脳全体というのは、これは、人体全体の1億分の50万ぐらいです、個数にして。 そして、質量にすると1億分の2百万程度みたいです。 それから神経細胞は、個数にすると人体の1億分の5万程度、それから質量にすると1億分の20万程度の様です。 それで、この、脳全体に比べて神経細胞というのが、なぜ1割程度しか無いのか、と言うと、これも、なんか、インターネットで調べてみますと、神経細胞以外の、その、神経細胞に栄養を供給したりだとか、そういうものが残りの9割を占めているのだそうです。 という事でですねえ、まあ社会の問題に置き換えますと、神経細胞の働きというのが、これが本来業務で、学問の研究などですねえ。 それに対して、神経細胞以外の、なんかグリア細胞とか言うらしいですが、それの行なってる働きというのが、これが学問の研究を補佐するような補助業務の様なもの、という風に考える事が出来るでしょう、と思いました。 ま、ただし、その、なんですか、学問の世界というのは、これは脳全体でもないですしね。 それから、だからこれは、あくまでその、社会における脳に相当する様な仕事、という風に考えなくてはいけないんであって、社会における脳に相当する様な仕事のほんの一部分が、たぶん学問のやってる事、学問の研究などだろう、と思います。 まあ、ですが参考には成るでしょう。 そのまま学問に何パーセントが来るべきか、という話までは出て来ませんが、参考には成るでしょう、という事で、これ、まあ、この結果から大雑把な見積もりみたいなものを考えて見ますと、社会の脳に相当する仕事(補助業務込み)には、全人口の0.5パーセントから2パーセントが従事し、全体の15パーセントから25パーセントの資金供給をすべき、という事が言えるんではないか、という、ええ、こういう大雑把な。 なんですかねぇ、ま、違ってる所は、追加的な研究によって、こう、明らかにして直して行って頂きたい、と思うわけですが、こういう路線で考えて行ってはどうか、という、なんですかねぇ、新しい切り口と考えて頂ければいい、と思います。 |
「なんですかねぇ、ま、違ってる所は、追加的な研究によって、こう、明らかにして直して行って頂きたい、と思うわけですが・・・」の部分は、聴講者から失笑らしきものが聞こえたので、それを受けて、間違ってる所があるのかなあ、と思って、述べた部分です。 |
| OHPで報告記事のアドレスを表示して | これは、まあ、この発表が終わった後、このアドレスに報告記事を書きます、という事なんです。 | サイト移転前の旧アドレスが表示されていただろう、と思います。 |
| - | ちょっと補足の話をしますと、仕分け論理というのは、たとえば学生時代に、気象に進む予定の学生、同級生ですが、素粒子論の様な分野は道楽だ、と言っていた事がありました。 ただし道楽という言葉は、私がその人の意を汲んで、私が発したものですが。 素粒子論より気象などが一段低く見られている事や、素粒子論を望んでも無理である事への負け惜しみだと感じたが、的確な言葉が直ぐに思い浮かばなかったので反論はしませんでした。 |
「役に立たない」という批判は自分に劣等感を与える存在への言い掛かりとして用いられがちだ、という話をしています。 04日@2011年09月@日記に参考記事があります。 |
| あとですねえ、まあ、これ、ちょっと時間配分間違えたかなあ。 う~ん、そうだなあ、まあいいか。 よく、汗水たらして働く、とかねえ、油まみれに成って働くとか、真っ黒に成って働くとか、そういう言葉がよく使われますが、まあ私はこういう言い方は嫌いでですねえ。 どうして嫌いかと言うと、そういうのしか仕事と認めない、みたいなねえ、排他的で偏狭な価値観を反映しているので、そういう表現は私は嫌いです。 まあ、そういうの仕分けの論理に通じるものだと思うんですが。 演劇じゃないんだから、見た目で働いている事のアリバイを作らなければならないなんて、そういう他人の足を引っ張れる社会にしてはいけない。 少し文章を練る時間が無かったので表現があまり適切じゃないですが。 |
「表現があまり適切じゃない」というのは、本当はもっと辛辣な言葉で表現したかった、という意味です。 辛辣に成り過ぎている、という意味ではありません。 「文章を練る時間が無かったので」というのは、辛辣さが足りないのは手加減によるものではなく言葉を選ぶ時間の不足による、という意味です。 |
|
| あとですねえ、私がこの発表の講演概要を提出した直後ぐらいに、テレビかなんかで誰かが、まあ政府の関係者か何かだと思いますが、そういういわゆる社会の脳に相当する様な働きの仕事とそうでない働きの仕事というものを固定するんじゃなくて交代制みたいにしてはどうか、みたいな事を、アイデアを出したという話を、テレビかなんかで見ましたが、そういうのなんかも、あれですよねえ、仕分けの論理みたいなものというのが本音においては、恵まれてない地位の人が恵まれている地位というものそのものを無くそうとする動き、だったんではないかと。 で、無くせないという事が分かったら今度は、ほんじゃあ代われと、交代しろと、言い出したみたいな事じゃあないか、というのを、そういうものを思ったりと、思いました。 |
末尾の「そういうものを思ったりと、思いました」は日本語的に少し変です。 「そういう事を思いました」か「そういう事を思ったりしました」と言うべきでした。 |
|
| それから、あと、大脳新皮質的な仕事への風当たりというのは、これは、文化人や知識人を目の敵にする共産化運動の特徴に似ているなあ、と思いました。 | - | |
| あとですねえ、そういうのがまあ仕分け論理の特徴ですが、それに対してまあ反論としたら、植物人間だって生きていると、まあ植物人間だって生きていて、そのためにはまあ脳の重要な部分の働きが停止している、その場合には停止しているわけですが、だから生きるためにはそれらは必要ないから、という事でそれらを必要ないとするのは暴論でしょうという、まあそういう言い方、が反論として一つ考えられると思います。 | 「植物人間だって生きているから生きるために大脳新皮質は必要なく、生きるために必要ないから大脳新皮質は必要ない」と言うと暴論に成る事から、必要という語の危険性を説いています。 | |
| あと、究極的にはですねえ、何故その脳というものが、まあ大脳新皮質なんかもそうですが、必要かと言うと、これは、これも私の専門外の話で、ちらっと聞きかじった話ですが、環境変化に適応するために脳の可塑性というものが是非とも必要なんでしょうね。 究極的には、これに由来するんでしょう、そういう大脳新皮質的な仕事の必要性というのは。 究極的には、こういうものに由来するんだと思います。 |
地球上の問題で言うと、資源がいつかは無く成る、とか、太陽もいつかは死ぬ、という環境変化が考えられる。 それらがずっと先の事でも、克服は不可能に近いぐらいに困難なので、今から本気で考えなくても間に合う、という保証は無い。 また、克服は不可能だ、と決めてかかるわけにも行かない。 問題が深刻化して来れば必ず考えるはずだ。 興味深さに引かれて考えるのでなければ、必要に押されて考えていたのでは、そういう問題の解決には到底及ばないだろう。 人間心理に好奇心が備わっている事には、それなりの進化論的な理由があるはずだ。 この活動に比して言うなら、経済活動なんてものは「一番難しい所はオレがやっておいたから、あとはお前らでも出来るだろ」といった程度の家事に過ぎない。 |
|
| あとですねえ、ノーベル賞学者の小柴さんなんかが、電子なんかを持ち出して、最初は必要性に気が付いてなかった事でも、あとで必要に成る事、大いに役に立つ事があります、という風に反論しておられるのは聞いた事があります。 これは有効な反論の一つだと思いますが、そういうものに対して「電子?でもそれだけでしょ?」と言う人が居るんじゃないか、と思ってね。 例えば、それじゃあ機械工学なんかは、これは間違いなくニュートン力学が役に立っていないわけがないわけで、あと量子力学だって物質設計に役に立っているでしょう。 それから最近では、一般相対性理論ですらGPSカーナビに役に立つ時代が来ている、らしいですねえ。 どんな先進的な物理学理論も、役に立つのが直ぐではないというだけであって、ずっと役に立たないものではない、と思います。 まだ実用化されていない様な学問の成果というのは、これは科学技術の潜在的可能性として蓄えられたものだ、という風に考える事が出来ると思います。 そして、近年は科学技術の進歩が目覚ましいというのは、裏を返せば、ものすごいスピードでそれを食い潰してしまう傾向がある、という事で、これは大脳新皮質的な仕事に大きな負荷をかける行為だ、と言えます。 その分、大脳新皮質的な仕事の重要性がますます高まっているんではないですか、という事ですね。 |
これは、環境変化というよりは、むしろ、経済成長の限界の観点からの、指摘です。 基礎物理学の研究は、経済成長の限界への到達を、延期する。 これは、「なあ、なんかもっとないの?」という市場からの声に応える力の源泉だ。 |
|
| 社会の何が人体の何に対応するか、塗り絵を完成させる問題が残るでしょう。 残ります。 まあ不完全な形で私が先ほど書きましたが、これを、もっときちっとしたものを書け、という問題ですねえ。 それから大脳新皮質を使う仕事イクオール社会の大脳新皮質、とは限りませんよねえ、ただしねえ。 そこら辺は、もう少し詳しく考えてみる必要がある、と思います。 |
ohp12au-13-2の対応図を充実させる問題を提起しています。 | |
| 人体において、ものすごく食糧が足りなく成ったり、呼吸が苦しく成ったりした時に、どこに優先的に酸素が回されるのか、といった、それも参考に成ると思うんです。 そもそも社会における仕分けの問題が出て来たというのは、財政がひっ迫して来たのでどこか削らなくちゃいけない、という事で出て来たわけで、これは人体においてどこが優先されるかというのは参考に成ると思います。 |
- | |
| あと、ただしですねえ、まあ、このような事を考えたからといって、これ全体主義にしろと言っているわけではなくて、全体主義は非常にいけない事なんだろうと、そういう価値観を私も共有しております。 戦時中の天皇機関説みたいな、そういうものはいけないんだろう、と思っております。 以上です。 |
実のところ私は、天皇機関説というのがどういうものなのか、良くは知らない。 戦時中の思想だから全体主義の一例なのだろう、と思って引用したが、知ったかぶりだった嫌いがある。 |
画像をクリックすると拡大表示されます。
| 講演概要 |  18aFG-2 |
日本物理学会講演概要集 第67巻 第2号 第2分冊 355ページより。 |
|
| OHP |  OHP-13-1 |
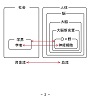 OHP-13-2 |
 OHP-13-3 |
質疑応答時間には、座長と私との間で、次の様な対話が行われた。
| 発言者 | 発言内容 | 注釈 |
| 座長 | この様なアナロジーを使って、例えば物理教育の問題などを考えて行くと、どの様な絵が見えて来る、という風に、考えておられますでしょうか? | - |
| 宇田 | 物理教育ねえ。 物理教育、それじゃあ、その、あれですねえ、あの、物理教育、学校教育などというのは、この中のどこかに対応するわけですが、で、こちらで言うとどれなのか、という事ですよねえ、うん。 そういう問題が見えて来る、と思います。 |
ここでは私は返答に窮しています。 最初、科学史の会場での講演を申し込んだら、物理教育の会場での発表を勧められ、物理教育会場での発表に変更しました。 本来は「物理と社会」というセッションで発表したかったのですが、今期は、このセッションがありませんでした。 |
| 座長 | 今後は特に、どういった方向で、これを発展させて行かれる、おつもりでしょうか? | - |
| 宇田 | 私は、これ、どちらかと言うと門外漢というか、自分の専門外の問題なので、単発に終わる可能性が強いです、ええ。 | - |