
since 2003
イレコナビ サイトマップ
| 攻撃技 | ||
| 気態用 | 液態用 | 固態用 |
| 蹴り | |||||
| ストレート | フォア フット |
バック フット |
サイド フット |
・・・ | |


ムエタイやキックボクシングの主力技である「ミドル・キック」は、空手語では「中段回し蹴り」だろう。
しかし、ムエタイやキック・ボクシングのミドル・キックは、厳密には空手の回し蹴りとは異なるらしいので、これらについては何か分かれば、三角蹴りのページに書く事にします。
私の分類では、インパクトの瞬間のエッヂの速度ベクトルが水平に近ければ「回し蹴り」、水平と大きく異なっていれば「三角蹴り」、と命名しておきます。
闘う神主TV[高松市キックボクシングトータルフィットネス繋]、というYouTubeチャンネルの、空手のハイとキックボクシングのハイの違い、という動画(https://youtu.be/iwls_QS0nRs)を見ると、やはりキックボクシングの「ミドル・キック」は回し蹴りではなく三角蹴りであるらしい事、が分かります。
その動画を見て、回し蹴りを使うのは回し蹴りでなければ通らない場合だけであり、出来るだけ三角蹴りで済ませる、必要も無いのに回し蹴りを使う事はしないのが正しい、と分かりました。
本当にその通りだ、と思った。
回し蹴りは三角蹴りよりもリーチが短い、回し蹴りは三角蹴りよりも弾着が遅く敵のパンチへのカウンターとして使うと間に合わない、と説明されていました。
空手の試合で何度も優勝した人が、回し蹴りは三角蹴りみたいに蹴れ、という風に指導するのを複数のYouTube動画で見たし、観戦解説動画でも「回し蹴りの軌道がよく絞れていて良い」といったような言葉を耳にしたので、回し蹴りよりは三角蹴りの方が使用機会が多い、三角蹴りを蹴るべき瞬間に回し蹴りを蹴るのは拙い、と見て間違いないでしょう。
回し蹴りには、障害物を迂回して標的に当てる事が出来る、標的への入射角を水平に出来る、という長所がある。
例えば、フォアフット前蹴上げで敵の頭部を蹴ろうとしたら、敵の胴が邪魔に成って蹴れないが、回し蹴りなら敵の胴という障害物を迂回して敵の頭部を蹴れる。
また、地面に垂直な棒を蹴るには、標的への入射角が水平であるのが最適だが、フォアフット前蹴上げではそう成らないのに対して、回し蹴りならそう成る。
地面に垂直な棒を回し蹴りで蹴る時には、距離だけ正しければ空振りも跳弾もしないのに対して、ストレート蹴りでは距離だけでなく旋回角まで正しくなければ空振りしてしまう。
これは、敵の胴や脚を蹴る場合に当てはまる。
敵の胴を蹴る場合、私の足・脚が敵の肘に当たってしまった場合に、三角蹴りでは私の足・脚が受けるダメージが大きく成りやすいが、回し蹴りならエッヂの速度ベクトルが水平に近いので私の足・脚が受けるダメージが大きく成りにくい。
回し蹴りには、ストレート蹴りよりも起動からインパクトまでの時間が長いという欠点や、接近中の敵に遠ざける向きの力を及ぼせない、という欠点がある。
回し蹴りは、ストレート蹴りよりもリーチも少し短い。
空手の回し蹴りは、空手以外の格闘技から取り入れた技で、元々は空手に回し蹴りという技は無かったと聞いたように記憶している。
だから、回し蹴りの蹴り方では、空手っぽくしようとする事にこだわると、ダメな技に成るのではないか。
| 始状態 |  |
 |
 |
| 蹴足離陸の瞬間 |  |
 |
 |
| インパクトの瞬間 |  |
 |
 |
| 着地完了(蹴り足を敵の近くへ降ろした場合) |  |
 |
 |
| 着地完了(蹴り足を敵から遠くへ降ろした場合) |  |
 |
 |
| 始状態 | レの字立ちから蹴り足のカカトを床から離して重心を回転軸上に置く。 |
| 蹴足離陸の瞬間 | 角運動量補給の説明で筋肉Aとされている筋群を伸ばした状態=回し蹴りの為のバネがしっかり貯まっているいる状態。 足腰は始状態と同じ。 それに加えて、全体として回転運動をしている。  始状態からこの状態への移行はほぼ腕の振りだけです。 肩は始状態よりも少しだけ回転させるが大きくは回転させない。 腕の振りは、しゃくる様に一瞬で行なう。 ここまで、腕の振りにではなく、蹴り足裏が地面から出来るだけ大きな静止摩擦力を受ける様にする事に意識を集中させ、そうするために無意識に腕を振ってしまう感じが正しい。 蹴り足と腰は最後まで後方に残し、蹴り足の離陸をギリギリまで遅らせる。 |
| インパクトの瞬間 | 横蹴りのインパクトの瞬間に似ている。 始状態から蹴り足離陸までと蹴り足離陸からインパクトまでを2つに分けて、2段ロケット、あるいは地震のP波とS波の様に意識する。 始状態からインパクトまでを一挙動として意識すると蹴り足の離陸が早く成り過ぎて角運動量補給が不十分に成ってしまったり、インパクトのタイミングが早く成り過ぎて標的への当たりが浅く成ってしまったりする。 標的に足を当てる場合は、インパクトの瞬間の足の速度ベクトルは、膝を伸ばす運動での足の速度ベクトルと同じぐらいの向き。 足の軌道の概念図の円の最高点よりも少し早い位置でインパクトが起こると意識すればよいのかも。 軸足が標的から離れる向きに傾いているのは、私の柔軟体操が足りないせいかもしれないが、回転軸の片方だけにウェイトが偏在していたのでは回転できない、蹴り脚の反対側にも蹴り脚と釣り合うだけのウェイトが分布していなければ回転できないという力学事情によるのかもしれない。 今後柔軟体操を進めながら確認を続けたい。 |
| 着地完了(蹴り足を敵の近くへ降ろした場合) | 蹴り足を後足とするレの字立ち。 敵の方を向いたままにすると股間接に無理な力が掛かる、と体感した。 右腕は脇腹ガード、左腕は逆側片目ガード。 |
| 着地完了(蹴り足を敵から遠くへ降ろした場合) | 蹴り足を後足とするレの字立ち。 左腕は脇腹ガード、右腕は逆側片目ガード。 蹴り足を前足とするレの字立ちを四つ足の構え第2状態後形として、これを着地完了姿勢にしようと考えた事も有るが、試しに動いてみると、蹴り足を後足とするレの字立ち=第2状態基本形を着地完了姿勢にする方が良いと分かった。  第2状態後形(着地) → 第2状態基本形(着地完了) 第2状態後形(着地) → 第2状態基本形(着地完了) ガード形成は、着地時にはまだ完了していなくてもよい、着地完了姿勢に間に合わせればよい。 |
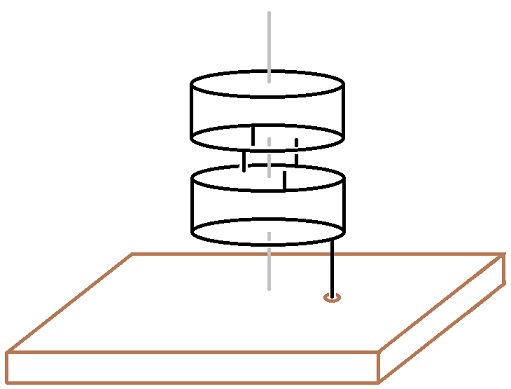
下図は、私が考える長回し蹴りのイメージです。
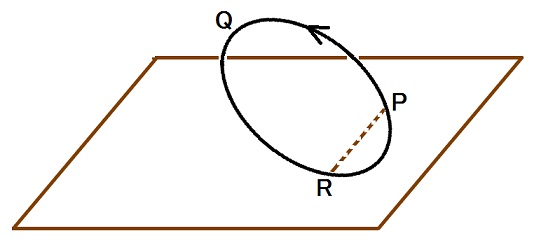
茶色の長方形は地面です。
黒線は、床に対して傾いた円で、茶色の破線の位置で床と交わっています。
最初はQを標的の位置だと考えていましたが、後で膝を伸ばす動きでの足の速度ベクトルが水平ではない事に気付き標的の位置はQよりも少しPに近い所にあると考える様に成りました。
標的に右足を当てる長回し蹴りは、Pから出発して黒色線に沿って円運動して標的に当たります。
実際の長回し蹴りは、このイメージに、膝の曲げ伸ばしの分だけ修正を加えれば、得られます。
また、フォロー・スルー(QからRまで)では上図の円に沿わず蹴り足を出来るだけ早く降ろせ、と佐藤嘉洋さんがYouTube動画で指導するのを見たので、その方式を私も多分採用すると思います。
しかし、インパクト前(PからQまで)は、フォロースルー(QからRまで)でも黒色線に沿って足を動かすつもりで居る方が、インパクトが強く成るだろうと私は思う。
空手の回し蹴りの基本稽古に見られる、脚を体の真横に抱え込んだ形は、足がPから出発してQに到着するまでの途中の瞬間状態だ、というのが私のスタイルです。
したがって、脚を体の真横に抱え込んだ形で一時停止する、という事は、私はやっていません。
ヘッド(エッヂ)は一方向にどんどん加速して行くべきだ、という考えを私は捨て切れない。
だから、ヘッドが途中で一時停止したり、ヘアピン・カーブを描いて動いたりする技には、私は懐疑的です。
私がカカト落としを嫌うのは、そのためです。
カカト落としでは、ヘッドが上端で折り返すので、それまでのヘッド加速が全部無駄に成ってしまいます。
私が考える長回し蹴りでは、脚を体の真横に抱え込んだ形は、運動中に一瞬見られる形だ、という風に成っています。
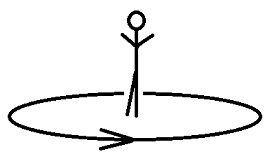
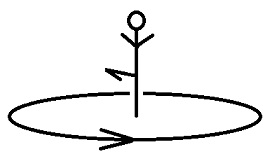
これは、敵から見ると、不動立ち(外八字立ち)から蹴り脚を真横に上げて抱え込み、続いて蹴り脚の膝を伸ばして蹴り足を真横に上げる動作をターン・テーブルの上で行なう様な蹴りです。
以下は、ターン・テーブルが回転していない場合の、あるいはターン・テーブルの上に立っている人に見える景色を描いた図です。
↓
↓
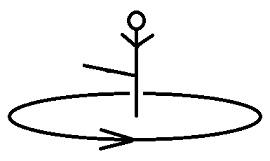
私がやっているタイプの長回し蹴りの模範は、根津優太という格闘家の実技に見る事が出来ます。
根津優太さんが何かの試合でリングに上がって直ぐ長回し蹴りを数回実行するのを見ましたが、どの試合だったかを後で調べておきます。
野球のバットのスウィングのニュアンスです。
私が考える長回し蹴りの基本は、全身回転の角運動量や運動エネルギーを標的に受けさせる、という考え方です。
この全身回転は、レの字立ち(後足のカカトを地面から離し、重心を前足のほぼ真上に乗せる形にレの字立ちを変形する)から蹴る場合、後足が地面から受ける摩擦力(地面に平行な力)によって生じます。
後足が地面から大きな摩擦力を受ける様にする事を「後足で地面を蹴る」という言葉で表現したいが、回し蹴りの場合、後足で地面を蹴る事は、(実際には私は足首を動かすように成ったけど考え方としては)足首の関節や膝関節を動かす事によってなされるのではなく、足・脚・腰を不動に保って、上体をひねる事によって行ないます。
足・脚・腰を不動に保って上体をひねれば腰を傷める危険が有るので、腕だけ振るつもりで、胴体のひねりは、腕を振ればどうしても自然に胴体も少しぐらいはねじれるよ、といった程度に留めます。
腕の振りはフォアバック同時打ちに似せますが、フォアバック同時打ちの様な全身連動はさせません。
この方法での回し蹴りを私は可変ターボ回し蹴りと名付けたい。
足・脚・腰を不動に保って腕を急速に振れば、全身の角運動量がゼロから幾らかまで変化し、その変化の速さが後足が地面から受ける摩擦力のモーメントに等しく成ります。
この事は、摩擦力がゼロならば、腕を急速に振っても足が滑って全身の角運動量はゼロのままである事を考えれば分かります。
摩擦力がゼロならば、、上半身が動いたのと逆の向きに下半身が同じだけ動くので、全体としてはプラス・マイナス・ゼロに成るわけです。
腕を振っている間、両足が地面に対して滑らなければ、後足が地面から摩擦力を受けている事を後足の足裏の触覚で感じる事が出来ます。
この時に、足・脚・腰を不動に保ち(残し)ながら、後足で地面を蹴っていると意識します。
この角加速は時間的には非常に短く、ギューではなくクッといった感じです。
長くとも「グイッ」まで。
これで角運動量の補給は完了です。
短前ストレート打ちではインパクトの瞬間に標的から受ける反作用に耐える為に後足で支えますが、回し蹴りでは支えが無い。
この支えの役割を果たすのが長回し蹴りでは全身の角運動量です。
胴の動きと脚の動きで挟む様にして蹴るという意識で長回し蹴りを蹴っている人も、挟む為のバネを貯める(脚と胴の前面を伸ばす)動作をする時に、後足が地面から摩擦力を受けて、その力のモーメントで全身に角運動量が発生している事でしょう。
バネ貯め動作終了時にこの角運動量相当の回転運動を自分で制動してしまうのはもったいない。
インパクトの瞬間は、全身回転(先述したターンテーブルに喩えられる)がどの位置まで回っているかと合っていなければ、威力が最大に成らない。
インパクトが早過ぎ(ターンテーブルが最適の向きに成る前にインパクトす)れば標的への当たりが浅い蹴りに、遅過ぎれば膝を伸ばす力を十分に活用できません。
当たりが浅いと言うのは、ストレートパンチで言うと、届かないパンチを無理して届かせた様な当たり方です。
標的へのエッヂのめり込みが少ないのが浅い当たり方です。
私は、自分がサンドバッグ蹴りでうっかり当たりの浅い蹴りに成ってしまいがちな事に気付き、インパクトを微妙に遅らせる様に意識しています。
下図の様に、上半身と下半身を2つのディスクで表し、AとBは筋肉で、後足の接地状態をON、OFFで表してみます。
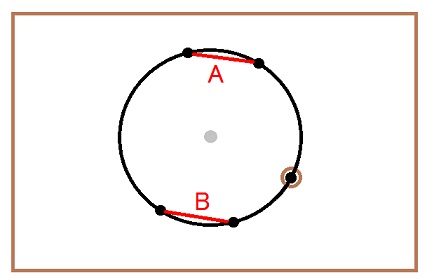
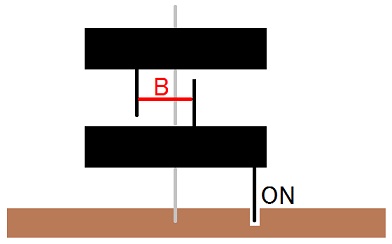
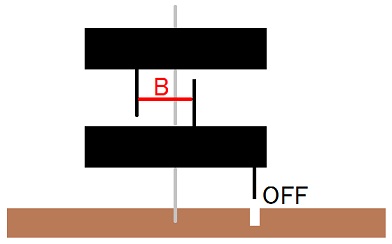
この時に後足が地面から水平な力を受けて、その分だけ上半身のディスクの角運動量(=2つのディスクの角運動量の合計)が増加します。
筋肉Bの収縮が終わると同時に後足の接地をOFFにすると、以後は角運動量保存の法則に従がって、2つのディスクの角運動量の合計は一定に保たれます。
この法則は筋肉Aや筋肉Bを働かせても働かせなくても成り立ちます。
後足の接地をOFFにしている期間中に筋肉Bの張力をOFFにして筋肉Aの張力をONにします。
すると、上半身のディスクの角運動量が減って下半身のディスクの角運動量が増えますが、この時に2つのディスクの角運動量の合計は一定に保たれるので、これは上半身のディスクの角運動量が下半身のディスクに移動する事だ、と言えます。
理屈としては、ここまでに書いた理屈だけで十分ですが、ホントにこんなので合ってるのかと疑問に思う人の為に、同じ事をクドクドと別の言葉で言い換えるレベルの補足説明を「ついでの話」として以下に書いておきます。
私はこっち(力学や物理学)が専門なので、(「実際の人体は2ディスク模型と違うだろうが」と言われれば「ええ、まあ、そりゃあ」という事に成るが)上記の2ディスク模型に限れば、これで絶対に間違いない事が私には明白に分かるのですが、「私は偉い物理学者だから信じろ」とか「力学というのは百年以上前に確立された理論であり百パーセント信頼できるものなんだよお」という言い方は、詐欺師でも出来るので、ここでは避けたいと思います。
私がここで使った理屈は、ニュートン力学とか古典力学と呼ばれる理論に基づいています。
ニュートン力学を詳しく知りたい人は私の物理学正典の「初等力学」パートで解説を読む事が出来ます。
ニュートン力学は、高校物理ないし大学1年生で習う物理学の理論です。
そういうある意味初歩的な学理なんですが、それですら、どうしてもこう成るんだ、ほんの少しでも変更すればつじつまが合わなく成るんだ、という事が分かる様に成るには、かなり勉強しないといけません、白帯から色帯に上がるぐらいだろうか。
そこで、スポーツや武道だけしかやらないつもりの人の為に、そういう勉強をしなくても「どうもこれは正しいみたいだぞ」という感覚を自分で持ってもらえる様な説明を、ここから書きます。
ニュートン力学というのは、百年以上前に確立された理論で、相対性理論みたいな事を言わなければ、どこをどう突いても絶対にボロは出ない完璧な理論、果てしなくつじつまが合い続ける理論です。
つまり、「あ?でも、この点についてはどうなんだ?」という疑問は、一見どれほどニュートン力学に含まれる間違いを暴き出しそうであっても、それを最後まで考え抜いて答えを出せば、ニュートン力学が正しい事の証拠のコレクションを1つ増やすだけです。
以下では、そういう「あ?でも、この点についてはどうなんだ?」的な話をします。
軸足の足裏が地面から受ける摩擦力のモーメントで全身の角運動量も少しは変化する、という事を言わなければ、角運動量保存の法則は成り立ちますが、筋肉を働かせるという要素が含まれているので、エネルギー保存の法則は成り立ちません。
だから、筋肉Aを働かせた時に上半身のディスクから下半身のディスクへ角運動量が移動する、という考えは正しいけれど、エネルギーが移動するという考えは間違ってます。
簡単のために上半身のディスクと下半身のディスクが形も大きさも重さも全く同じである場合で説明します。
上半身のディスクと下半身のディスクの角速度が同じに成るまで筋肉Aを使うと、角速度は最初(後足の接地をOFFにした瞬間)の上半身のディスクの角速度の半分に成り、2つのディスクの角運動量の合計は最初と同じですが、2つのディスクの運動エネルギーの合計は最初の半分に減ります。
これは、(角運動量) = (慣性モーメント)×(角速度)、(運動エネルギー) = (慣性モーメント)×(角速度の2乗)÷2、だからです。
角速度が半分に成れば、運動エネルギーは4分の1に成るので、それを2つ足し合わせても元の運動エネルギーの半分にしか成らないわけです。
上半身のディスクの角速度がゼロに成るまで筋肉Aを使うと、下半身のディスクの角速度は上半身のディスクの最初の角速度と同じに成り、この場合は、角運動量の合計も運動エネルギーの合計も最初と同じに成り、誤ってエネルギー保存の法則を使って計算してしまった場合と答えは同じに成ります。
筋肉Aをもっと使って、上半身のディスクの角速度がマイナスに成る(上半身のディスクが逆回転する)様にする、例えば、上半身のディスクの角速度が最初の角速度×(-1)、下半身のディスクの角速度が最初の上半身のディスクの角速度×2に成る様にすると、2つのディスクの角運動量の合計は最初と同じですが、2つのディスクの運動エネルギーの合計は最初の5倍に増えます。
この様に、途中で筋肉を使うと、エネルギーの合計は色々に成ってしまうわけです。
この「ついでの話」を書き始める直前に私は、「あれ?筋肉がした仕事の分だけ全体の運動エネルギーが増えるんじゃなかったっけ?」と疑問に思いました。
それが、「ついでの話」を書き始めた動機です。
つまり、筋肉Aを収縮させれば筋肉Aが2つのディスクに仕事をし、その分だけ2つのディスクの運動エネルギーの合計は増えるはずなのに、実際にはしばらくは運動エネルギーの合計が減り続ける、あれ?おかしいぞ!と思ってしまったわけです。
筋肉を使っても2つのディスクの角速度を揃える場合には運動エネルギーの合計が減る、という事情は、この問題を非弾性衝突の回転版だと考えれば、自然な事に思えます。
高校物理で習う非弾性衝突は並進版だと言う事が出来るでしょう。
筋肉がした仕事の分だけ運動エネルギーが増える、というのは正しいんだけど、筋肉がマイナスの仕事をする(上半身のディスクにする仕事と下半身のディスクにする仕事の合計がマイナスだ)という事です。
筋肉Aがした仕事がマイナスに成り得るのは、後足の接地をOFFにしてから下半身のディスクの角速度が上半身のディスクの角速度に追い着く(=と等しく成る)までは筋肉Aは伸び続けるのであって最初から収縮を開始する(筋肉Aは張力をONにすると同時に長さが増加から減少に転じる)わけではないからです。
| 時↓ 間↓ 経↓ 過↓ |
後足の接地状態 | 筋肉A | 筋肉B | 上半身の 角速度 |
下半身の 角速度 |
|||
| 張力 | 長さ | 張力 | 長さ | |||||
| ON | OFF | 増加 |
ON | 減少 |
増加 | ゼロ | ||
OFF |
ON |
OFF |
減少 |
増加 |
||||
| 減少 | 増加 | |||||||
2025年05月18日には私は、この点を考え落としていたせいで、次の様な間違った事を書いてしまいました。
| 筋肉がした仕事がプラスに見えるのは、筋肉の中心やどちらかの端が静止している様に見える座標系で計っての事であり、それ以外の座標系ではそうは成らない、仕事も運動エネルギーも座標系非依存ではない、う~ん、段々思い出して来たぞ。 |
この枠内の考えは間違っています。
正しくは、非相対論的な力学では筋肉がした仕事は座標系非依存です。
したがって筋肉が収縮する時には必ず周囲にプラスの仕事をしてその分だけ周囲のエネルギーを増やします。
筋肉が周囲からエネルギーを奪うのは、筋肉が伸ばされる時だけです。
この枠内の私の考えの間違い方は、人間の思考のカッコ悪い間違い方の1つの典型例であり、人間の思考の特徴を研究したり説明したりする為の資料として利用価値が高いと思うので、ここに展示しておきます。
今回のカッコ悪い間違い方というのは、問題を大きく考え過ぎる事です。
似た例としては、量子力学の解釈問題に対する多世界説を挙げる事が出来ます。
社会の問題なんかでも、何でも直ぐに根本が間違っているからだと早合点するのも、問題を大きく考え過ぎる事に当たり、共産主義はその具体例の1つだろう。
筋肉Aは最初から収縮を開始するわけではないという事も、気付かなければ、ニュートン力学の理論が間違っているから答えが合わないんだ、という早合点の原因に成り得ます。
だから、この点も、ニュートン力学はやっぱりどこも間違ってないんだ、という事が分かる様に成る道の険しさを表している、と言えるでしょう。
この事は、社会制度についてのニセ旗工作という概念を説明する好例です。
例えば、酒を飲んで自動車を運転して故意に人身への衝突を起こすキャンペーンを行なえば、飲酒運転に甘い法律や社会制度を悪者にする事が出来ます。
本当は、そういうキャンペーンを行なった人々が悪いのに、この事情を知らない大勢の人々は、飲酒運転に甘い法律や社会制度が悪いんだ、という考えにミスリードされるわけです。
そう成る様に狙って犯罪するのが、社会制度についてのニセ旗工作です。
途中で「筋肉がした仕事」という言葉を私は使いましたが、これにおける「仕事」とは(力の大きさ)×(力の向きに移動させた距離)の事で、高校物理で習います。
筋肉の場合、筋肉の片方の端が外部にする仕事は、それを計る座標系によって異なりますが、筋肉の両端が外部にする仕事の合計は(筋肉の張力)×(筋肉の長さの減少)に等しく成り、これは座標系非依存です。
筋肉Bの張力をONにすると同時に後足が地面から水平な力を受け始める事は、下半身のディスクが受ける力の釣り合いを考えれば分かります。
後足の接地がONの期間中は、下半身のディスクは静止したままなのだから、下半身のディスクに働く力は釣り合っていなければいけません。
したがって、下半身のディスクが筋肉Bから受ける力(のモーメント)と地面から受ける力(のモーメント)は釣り合っているわけです。
ついでの話の、そのまたついでの話に成りますが、それではエネルギー保存の法則というのはいつでも成り立っているわけではないのか?という風に疑問に思う人が居ると思います。
運動エネルギーに限ればいつでも成り立っているわけではありません。
しかし、化学エネルギーや熱エネルギーなど全てのエネルギーをカウントすれば、いつでも成り立っています。
例えば筋肉Aが2つのディスクに仕事をするとき、大体の考え方は、筋肉Aの内部に蓄えられている化学エネルギー(グリコーゲンが持っているエネルギー)が減り、その分だけ筋肉Aは2つのディスクに仕事をする、その仕事の分だけ2つのディスクの運動エネルギーが増える、したがって、(筋肉Aの内部に蓄えられている化学エネルギー) + (2つのディスクの運動エネルギーの合計) は変化しない、という風に成ります。
これに熱エネルギーの要素を加味すれば、エネルギー保存の法則の正確な表現に成ります。
理屈を最小限にして理解したい場合は、上半身をスネだと思い下半身を足だと思うとか、上半身を大腿だと思い下半身をスネだと思えば、感じをつかめます。
垂直ジャンプで、足首だけを利かせてジャンプする事も、膝だけを利かせてジャンプする事も出来ますよね。
同様に、上体起こしだけを利かせてジャンプしようとする力を得る事も可能ですよね。
これでは力不足で足裏が地面から離れるには至らないだろうけど、それでも、ジャンプしようとする力は得られる。
これの回転版を考えているのが上記の2ディスク模型です。
長回し蹴りの序盤の角運動量補給の方法として、フォアバック同時打ちの様な全身連動(後足接地がONの期間中に下半身のディスクも回転させる)を使う事も可能ですが、それは変則的な方法だとしておきます。
後足接地がONの期間中に下半身のディスクも回転させる方式には角運動量補給に時間が多く掛かる、というデメリットが有ります。
その点、腕だけなら幾らでもと言って良いぐらい速く動かせます。
思ったより速く動かせるので、つい最高速以下で振ってしまいがちですが、腕は最高速で振らないと損です。
最高速で振っても何もデメリットは有りません。
また、後足接地がONの期間中は下半身のディスクを回転させない方式でも、腕を回転軸から出来るだけ離して振れば、角運動量をかなり多く補給できます。
これは、(慣性モーメント) = (質量)×(回転軸からの距離の2乗) であるために腕の慣性モーメントが馬鹿に成らないぐらい大きいからです。
「質量」というのは「重さ」とは違うんだけど、分からない人は「重さ」だと思って下さい。
(回転軸からの距離) = (腕の長さ) でもありません。
腕の各部位(微小部位)について (慣性モーメント) = (質量)×(回転軸からの距離の2乗) を考え、それを全ての微小部位について足します(積分って言うんだけどね)。
だから、腕の振りで手指先を伸ばす事によって慣性モーメントを少しでも大きくするという工夫にも、気休め以上の効果が有ります。
以上の事と全身連動には時間が掛かる事を考え合わせて私は、長回し蹴りの角運動量補給で全身連動を使うのは基本的ではない、と判断しました。
慣性モーメントを最大化しての腕の振りは下図のごとくです。
根幹は以下の2→3です。
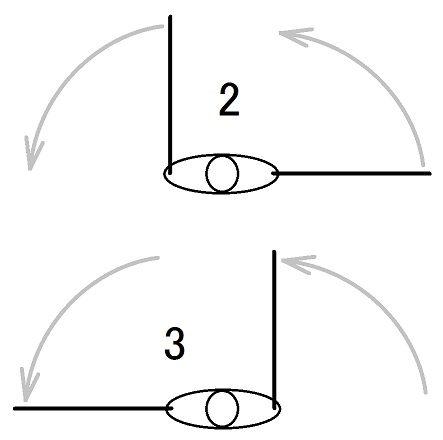
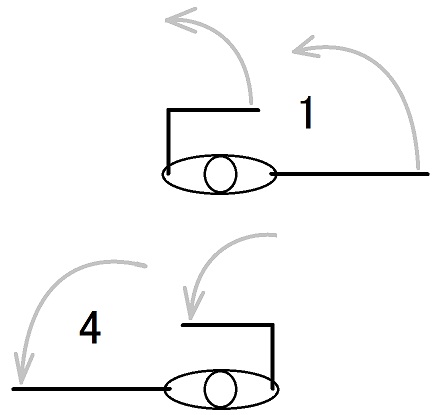
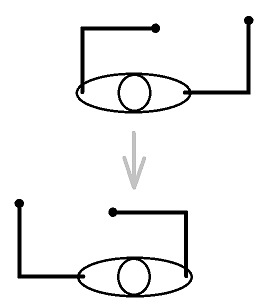
脇を開ければ開けるほど、また、肘を伸ばせば伸ばすほど、腕を振った時に角運動量を多く補給できます。
しかし、そうすればするほど動作が緩慢に成るので、戦局に応じて、角運動量の補給と早さのどちらをどれだけ優先させるかの選択をする必要が有ります。
私が「可変ターボ」と名付けたのは、そのためです。
ここまでの腕の振り方のエッセンスを保持したまま、各人が自分の好きな形にカスタマイズするのも良いと思います。
慣性モーメントを少しでも大きくする事に意味が有るのは、後足の接地がONの間だけです。
後足の接地がOFFの期間中は、腕の使い方とは無関係に角運動量保存の法則が成り立ちます。
だから、後足の接地がOFFで腕と胴の位置関係が変化しない期間中には、慣性モーメントが小さい方が角速度は大きく成ります。
(角運動量) = (慣性モーメント)×(角速度) だからです。
これは、フィギュア・スケートのスピンを例に取って説明される事が多いポピュラーな物理です。
したがって、膝を伸ばして脚を上げているインパクトの瞬間には、全身回転の角速度はかなり小さく成っいます。
それでも、足の速さは(角速度の大きさ)×(脚の長さ)だから、離陸直後の蹴り足の速さと同程度です。
これはあまり大きくないけれど、角速度がほとんどゼロに成るのとは対照的に、足の速さはほとんど元のままです。
この様な全身回転に伴う蹴り足の速度ベクトルに膝を伸ばす運動の速度ベクトルを加算した結果がインパクト時の蹴り足の速度ベクトルです。
角速度は非常に小さく成るけれど角運動量はしっかり保たれているので、外見上は同じに見えても、角運動量補給が有る場合と無い場合では、インパクトの力感に大きな差が生じます。
インパクトの瞬間だけは、標的から受ける力(のモーメント)によって全身の角運動量が出来るだけ大きく減る様にしたい。
これは、標的に出来るだけ大きな力積を受けさせる様にする事と同じだからです。
その為には、インパクトの瞬間には腕を後足の接地がONの期間中の様に振ってはいけない。
腕を逆向きに振る必要は無い、腕を胴に密着させる形に畳んでしまっていてもよいけれど、後足の接地がONの期間中の様に振るのはNGです。
YouTubeの回し蹴りの解説動画で上田幹雄さんが「腕を順方向に振るとそっちに力が逃げる」と言っていたのは、その事を体感しての事だろうと思います。
(全身の角運動量の減少) = (エッヂが標的から受けた力のモーメント)×(接触時間)
この事と作用反作用の法則を考え合わせれば、標的に出来るだけ大きな衝撃を与える事と、全身の角運動量をインパクトで出来るだけ減らす事とは同じです。
インパクト終了時にまだ腕が順方向に回転運動をしていれば、その分だけ全身の角運動量がまだ残っている事に成り、標的に与える衝撃が最大化されません。
他の方式では出来ないというわけではないんだけど、全身回転を使う私のターボ方式では、敵が私の蹴り脚をキャッチする事を、どじょうすくいみたいにして難しくする事が出来ます。
威力を最大にすると標的からの反作用で全身回転が止まってしまうけれど、威力を少し減らしたり、蹴るのを断念したりして全身回転を残しておけば、蹴り脚を回転方向にスルリと抜く事ができます。
プルバック方式ではキャッチを免れません。
また、全身回転を使う私のターボ方式では、吸収ステップで逃げる敵を深追いして蹴る事も出来ます。
2024年10月05日までの練習実感としては、回し蹴りでは軸足の爪先の向きをしっかり先行させ、素振り着地では敵に背を向けるぐらいでなければ、股関節付近に無理な力が掛かる、と感じる。
これは私の股割り等の柔軟性が不十分だからかもしれないので、今後柔軟性をもっと高めながら確認を続けたい。
股関節の使い方の注意点は回し蹴りでも横蹴りの場合と同じなのか否か検討中です。
着地姿勢はいずれもフォロースルーの回転方向に詰めたレの字立ち。
「スネ」は長さの尺度@デザイン方法論で定義されています。
実際に蹴ってみて気持ち良く蹴れた位置関係でのサンドバッグのインパクト前の表面位置の直下から軸足の接地点(中指の中足趾節関節)までの距離を測定した。
| エッヂ | 評価 | 説明 | 標的 | ||
| 強度 | 向き | 総合 | |||
| 足前底 | △ | 敵の胴を蹴る場合には、エッヂとしては出来るだけ足前底(中足)を使いたい。 革靴を履いている場合には爪先で蹴る。 胴を蹴るには接触面積の小さい足前底が適している、というコメントを、総合格闘技の試合中の解説で聞いたことがある。 2014年07月21日に東京・大田区総合体育館で開催されたDEEP CAGE IMPACT 2014の中の岡野裕城と白井祐矢の対戦中に解説者の熊久保英幸さんが「面(スネ)よりも点(中足)の方が絶対にダメージが大きい」と発言するのを聞いて「やっぱりそうか」と思った。 昔の空手の教本の回し蹴りの解説部分には決まって、標的に足前底を当てる回し蹴りが書かれていました。 その流れが変わって、足甲(背足)を標的に当てる回し蹴りが主流に成ったのは、芦原空手の教本あたりからだと思う。 試合ではもっと前から足甲が主流だったかもしれないけど。 インパクトの瞬間の形は、普通にやると、足前底が少し水平よりも上に向いてしまう。 足前底が標的を水平に蹴り抜く様にするには、軸脚と腰の回転を少し超過させるとか、エッヂとして足刀の足指を反らした形を作るとか、何か工夫する必要が有る。 金澤弘和さんだったか、大家の回し蹴り写真で、エッヂとして足刀の足指を反らした形が使われているのを見た事が有るが、それは、この問題に由来するだろう。 エッヂとして足刀の足指を反らした形を使っても、膝を伸ばす運動によるエッヂの速度ベクトルは水平よりも少し上を向いてしまう。 軸脚と腰の回転を少し超過させるやり方では、標的から受ける反作用によって全身の角運動量を減らすのがソフトに成ってしまう気がする。 だから、どちらも私は少し嫌だと感じる。 インパクトの瞬間に足前底も足前底の速度ベクトルも水平より少し上を向く普通の蹴り方で行こうかと私は考えているが、もっと良い方法が無いかも考え続けたい。   普通にやると爪先が水平に向かない、膝も水平に向いていない。  軸脚と腰の回転を超過させれば、膝も爪先も水平に向く。 軸脚と腰の回転を超過させれば、膝も爪先も水平に向く。足刀の足指を反らすだけでは、爪先は水平に向くが膝は水平に向かない。   インパクトの瞬間の足前底の速度ベクトルの向きと足前底の向きを一致させるのが正しい、という基準と、インパクトの瞬間には足前底の速度ベクトルの全身回転成分は小さく、足前底の速度ベクトルは膝を伸ばす運動の成分だけで近似できるので膝も爪先も水平に向かない普通のやり方でよい、と考えてみた。 2025年12月に素振り練習で、インパクトの瞬間に蹴り足の爪先が水平よりも少し上を向いているのに蹴り足の速度ベクトルを水平に向ける様に蹴ったら股関節が痛かった。 ついついそういう風に蹴ってしまう事が多い。 全身は地面に垂直な軸の周りに回転しているのに蹴り足の速度ベクトルは水平にしない、というのは本能に反する、練習が必要だ、と実感した。 |
|||
| 足甲 | 〇 | 敵の首や頭部を蹴るのは足甲でもよい | |||
| スネ | ◎ | スネの足首に近い部分や膝に近い部分を標的に当てる場合には、脚のネジレ角を、足前底を標的に当てる場合と同じにして、スネ骨の稜線を標的に当てる。 スネの足首からも膝からも遠い部分を標的に当てる場合には、脚のネジレ角を、足爪先がやや上を向く角にし、スネ骨の内側斜面を標的に当てる。 スネで蹴らないと足で蹴ると骨折などの怪我をしますよ、という話も聞こえている。 足甲(背足)、足前底(中足)、スネの足首に近い部分を標的に当てる場合には膝の曲げ伸ばしを行なうが、スネの足首から遠い部分を標的に当てる場合には膝を伸ばしたまま蹴るのが普通である。 標的に足を当てる回し蹴りと違って、スネ骨の内側斜面を標的に当てる回し蹴りでは、標的から受ける反作用力が膝を曲げる向きではなく若干膝を折る向きなので、インパクト時には膝にシッカリと力を入れておく必要が有るだろう。 標的に足を当てる蹴りと違って、標的にスネを当てる蹴りには、高い標的を蹴る時に非常に大きな股関節の柔軟性が必要に成る、敵との距離が近く敵のパンチが届いてしまう、という欠点が有る。 蹴り技の重さは、標的に足を当てるよりもスネを当てる方が重く出来る。 |
|||
| 膝 | ◎ | モモ膝(太ももの膝部分)を標的に当てる。 標的にスネを当てる場合よりも、高さを出すのがさらに難しく成る。 |
|||
| 実 例 |
日時 | 場所 | 大会 | 当事者(名前/体重) | 防具 | ラウンド | タイミング | エッヂ | 被撃部位 | 入射角度 | 直前事・ 被撃姿勢 |
注釈 | ||
| 攻撃者 | 被撃者 | |||||||||||||
| クリーン・ヒット K.O. | ||||||||||||||
| クリーン・ヒット 有効 | ||||||||||||||
| クリーン・ヒット 無効 | ||||||||||||||
| 空振り | ||||||||||||||
中段回し蹴り(足前底をペットボトルに当てた)2025年08月10日撮影分@蹴り@空手の技@動画
回し蹴りの角運動量補給(実演)2025年05月27日撮影分@蹴り@空手の技@動画
このページの下書き