
since 2003
イレコナビ サイトマップ
日本物理学会2016年春季大会での私の発表は、文法物理学についての19aAG-2「離散化された宇田方程式の解」および物理教育についての19pBB-12「学問、教育とカネの問題」の2つだった。
今回は、発表旅行中に写真を全く撮影しませんでした。
AG会場は、東北学院大学泉キャンパス2号館2階223教室だった。
19aAG-2「離散化された宇田方程式の解」では、液晶プロジェクターで資料を掲示しながら、次の様に口述した。
| 発言タイミング | 発言内容 |
| OHP-sr-1 | 宇田雄一です。 離散化された宇田方程式の解を発表します。 |
| OHP-sr-2 | 宇田方程式というのは、(冒頭の式を指して)これです。 (最上段の第2式を指して)χ(□-ε)は、tをχ(t-ε)に写す関数です。 この方程式を離散化するために、関数χを、(離散化の段の第1式を指して)この様な無限数列で置き換え、汎関数Φを、(離散化の段の第3式を指して)この様な多変数関数で置き換えます。 ただし、数列の各項は関数χを使って、(離散化の段の第2式を指して)この様に定義されます。 すると、宇田方程式の(破線の上の段の式の最左辺を指して)この部分は、(破線の上の段の式の最右辺を指して)この様に離散化されます。 宇田方程式の(破線の下の段の式の左辺を指して)この部分は、(破線の下の段の式の右辺を指して)この様に離散化されます。 |
| OHP-sr-3 | (冒頭の2つの式を指して)これは、変数を無限数列χから無限数列の組a, bに変換する、変数変換の式です。 この変数変換によって、関数Φは(最上段の第3式を指して)この式で定まる関数Fに変換されます。 宇田方程式の(実線の下の段の第1式の最左辺を指して)この部分は、(実線の下の段の第1式の最右辺を指して)この様な式に変換されます。 したがって、宇田方程式のこの部分は(実線の下の段の第2式の最左辺を指した)、(実線の下の段の第2式の最右辺を指して)この様な式に変換されます。 χkcos(kπ/n) が an に成り、ここを見ますね、χksin(kπ/n) が bn に成る事は、計算なしで分かるので、χk-1cos(kπ/n) と χk-1sin(kπ/n) を計算します。 |
| OHP-sr-4 | χk-1cos(kπ/n) の和を計算すると、(上段の式の最右辺を指して)こう成ります。 (上段の2行目を指して)まず、シグマ和の番号を1つだけズラします。 次に、三角関数の加法定理を適用します(上段の3行目を指した)。 すると、χkcos(kπ/n) が an, χksin(kπ/n) が bn だから、こう成ります(上段の式の最右辺を指した)。 (実線の下の段を指して)χk-1sin(kπ/n) の和の計算も、同様です。 |
| OHP-sr-5 | 以上の計算結果を(OHP-sr-3末の式を指して)この式に代入すると、(OHP-sr-5冒頭の式を指して)この式が得られます。 (OHP-sr-5の実線の下の段の第1式の最左辺を指して)χkでの偏微分をanでの偏微分とbnでの偏微分を使って表現し直すと、こう成ります(OHP-sr-5の実線の下の段の第1式の最右辺を指した)。 (∂an/∂χkを指して)これが[cos(kπ/n)を指して]これに成る事は、(OHP-sr-3の第1式を指して)この式から分かり、そして、(∂bn/∂χkを指して)これが[sin(kπ/n)を指して]これに成る事は、(OHP-sr-3の第2式を指して)この式から分かります。 結果を2回くりかえし使う事によって、(OHP-sr-5の最後の式を指して)この式が得られます。 次に、(OHP-sr-5の最後の式の右辺の三角関数の因子を指して)この部分のkでの和を計算します。 |
| OHP-sr-6 | (1行目と2行目を結ぶ等号を指して)この等号の成立は、(2行目の三角関数部分を指して)この部分に三角関数の加法定理を使う事によって、確める事ができます。 (3行目の1を指して)この1は、k = 0 の項です。 残りの(3行目のΣ和を指して)この部分は、(2行目の三角関数部分を指して)この部分がkの偶関数である事から、kがプラスの項だけ取って、係数を2倍にした物です。 ここで、(下向きの矢印の右に書かれている式を指して)こういう和の公式を使うと、結果は(実線の上の段の最終行を指して)こう成ります。 (∞を指して)この∞は、自然数の個数です。 Nを無限大に持って行った時に{sin[(N+1/2)a]を指して}この部分がゼロに成る、と見なしました。 そうしてもよいのか不安です。 (実線の下の段を指して)途中で1が登場しない等の違いがありますが、この和の計算も、同様です。 |
| OHP-sr-7 | (冒頭の式を指して)この和の計算でも、(1行目と2行目を結ぶ等号を指して)この等号の成立は、三角関数の加法定理を使って確められます。 (2行目の三角関数部分を指して)この部分は、kについて奇関数だし、k=0での値もゼロなので、全体としてゼロに成ります。 同様に(破線で挟まれた段の式を指して)この和もゼロに成ります。 以上の計算結果を、(OHP-sr-5の最後の式を指して)この式に代入すると、(OHP-sr-7の破線と実線で挟まれた段の1行目の等号を指して)この等号の成立が分かります。 さらにsで和を取ると、こう成ります(OHP-sr-7の破線と実線で挟まれた段の式の最右辺を指した)。 この計算結果を(OHP-sr-2の最後の式の右辺を指して)ここに代入し、得られた結果で、宇田方程式の右辺の(OHP-sr-2の最後の式の左辺を指して)この部分を置き換えます。 これは、(OHP-sr-2の冒頭の式の右辺を指して)この部分です。 宇田方程式の左辺については、(OHP-sr-5の冒頭の式を指して)この式で、宇田方程式の左辺の(OHP-sr-2の実線と破線で挟まれている段の最左辺を指して)この部分を置き換えます。 これは、(OHP-sr-2の冒頭の式の左辺を指して)この部分です。 すると、宇田方程式は、(OHP-sr-7の最後の式を指して)こういう形に離散化されます。 |
| OHP-sr-8 | (冒頭の2つの式を指して)βn とγn を、この様に定義します。 すると、離散化された宇田方程式は、(第3式を指して)この様に書けます。 ここから、この方程式の解を求める作業に移りますが、一般解を求めるのではなく、Fがこの様に(実線の下の段の第1式を指した)単一のan, bn対のみの関数である場合だけを考えます。 この場合、Σ和が外れて、スモール f に対する方程式は(最後の式を指して)こう成ります。 |
| OHP-sr-9 | スモール f を求める為に、f をフーリエ展開し、f に対する条件をこの係数 g (第1式中のgを指した)に対する条件に変換します。 この式を(OHP-sr-8の最後の式を指して)この式に代入して部分積分を使うと、g に対する条件として、(OHP-sr-9の第2式を指して)この式が得られます。 部分積分を使った点が不安です。 因子の順序を変えると、p と p での微分の交換関係、および q と q での微分の交換関係から、(OHP-sr-9の第3式中の2βを指して)この2βが出ます。 さらに、項の並べ替えを行なうと、(OHP-sr-9の第4式を指して)この式が得られます。 極座標を導入して、さらに書き換えると、解くべき方程式は、(OHP-sr-9の中段の最終式を指して)こう成ります。 使っているのは極座標なので、θが2π進むと関数の値は元に戻らなければいけません。 従って、解は、(下段の第1式を指して)この形に成るはずです。 この式を(OHP-sr-9の中段の最終式を指して)この式に代入すると、Rk についての(OHP-sr-9の下段の第2式を指して)こういう方程式が得られます。 これを解くと、(OHP-sr-9の下段の第3式を指して)こういう解が得られました。 講演概要の式は間違いです。 講演概要を書くときには、(OHP-sr-9の下段の第2式中のβrを指して)このβrを見落として、(OHP-sr-9の末尾の式を指して)こういう風にやってしまいました。 |
画像をクリックすると拡大画像が表示されます。
| 講演概要 |  19aAG-2 |
日本物理学会第71回年次大会(2016年)概要集 Web版ISSN2189-0803 DVD版ISSN2189-079X 2ページ |
|||
| OHP |  OHP-sr-1 |
 OHP-sr-2 |
 OHP-sr-3 |
 OHP-sr-4 |
 OHP-sr-5 |
 OHP-sr-6 |
 OHP-sr-7 |
 OHP-sr-8 |
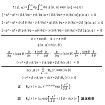 OHP-sr-9 |
||
2016年03月19日撮影分(素粒子論)@学会発表の実況@動画
この発表の原型はwww.GrammaticalPhysics.ac > Forum > Problems > Theory of Quantum History Entangled in Time-like Direction > Discretized Quantum Mechanical Solutionです。
質疑応答時間には、次の様な対話が生じました。
| 発言者 | 発言内容 | 注釈 |
| 鈴木 | その宇田理論って言うのはね、結局私も吸着でもって苛められたんだけれども、結果論じゃないか、って事なんですよね。 だけど、その理論をニュートンの万有引力の法則に適用してみてね、そいで、それと比較する事によって、私が言う所の吸着の理論は、まあ生きたんじゃないかと、こう感じるわけ。 ですからその、宇田理論もね、計算した結果こう成ると言うのは、そういう結果論であってね、もっとこう、何て言うかなあ、微分でない数学の解き方をしてみて、同し内容をね、それで、その結果こういう相対的な物が得られたんだよ、というね、そういう結果を出さなければね、理論として独立できないんじゃないか、と思うんですよね。 |
|
| 宇田 | 全然そうは思いません。 | |
| 鈴木 | いかん。 | 謎の発言。 |
| 座長 | 今回の話ので、今回の研究の動機として、なぜ離散化した方程式を研究しようと、思われたんでしょうか? 元々の方程式は、なかなか解き難い等の理由があるんでしょうか? |
|
| 宇田 | そうです。 そのまま解くのが出来なかったので、仕方がないので、離散化したものをチョッと考えて見た、という事です。 |
|
| 座長 | 数値的にも、やっぱり解くという事は難しい、という事なんでしょうか? | |
| 宇田 | 数値的は、むしろ私が、それをする技術を、持っておりません。 | |
| 座長 | ああ、そうですか。 じゃ、もしかしたら、この離散化されて解いた解と数値解を比べると、妥当性みたいな物が評価できる可能性はある、という事でしょうか? |
|
| 宇田 | ああ、可能性はある、と思います。 ついでの話なんですが、この発表内容を考えた後に、離散化とか近似とか、そういう物を使わずに、厳密解を求める事に成功したので、次回はそれを発表したいなと、 |
|
| 座長 | じゃ、次の宮崎の学会で、お願いします。 | |
| 宇田 | はい。 |
19aAG-3「場の量子論はなぜ正しい結論を与えるか」の質疑応答時間に質問した。
その内容は以下。
| 宇田 | 「アンチノミー」という言葉の意味が分かりませんん。 | |
| 吉田(発表者) | 二律背反、同一の原理から二つの矛盾した結論が導き出される事です。 | |
| 宇田 | 特殊相対性理論はアンチノミーである、という事は、相対性理論は間違っている、という前提の下での議論ですか? | |
| 吉田 | 前提じゃなくて、相対性理論が間違っている事は、前回発表しました。 そこで根拠も示しました。 |
この人の前回の発表は、日本物理学会2015年秋季大会25pSC-3です。 この発表の質疑応答時間に私は紙に斜交座標を書いて、発表者にそれを見せ、それを根拠にした反論を行ないました。 発表者がx=0とx'=0が一致しない事を矛盾だと言ったからです。 従って、左記で「根拠」だとされている主張は、既に論駁されています。 |
| 宇田 | 今回の発表内容は、前回のそういう発表内容に基づく議論だ、という事ですか? | 「前提」という言葉の選択も間違ってないはずだが、言い直した。 |
| 吉田 | そうです。 | |
| 宇田 | 有難うございます。 | 前回の発表内容を即座には引用できないので、これ以上の質問はしなかった。 これでも、この発表に対する他の聴講者の理解の助けに成ったと思う。 |
19aAG-4「ブレーン模型に見る物質粒子の新規な存在様式、及びその人工知能理論への応用」の質疑応答時間にも、批判的な観点を私以外の聴講者にも持ってもらう為に、次の様な質問をした。
| 前半の素粒子論の話と、後半の心理学の話のつながりが分かりません。 |
この後、発表に含まれていた
| 自動販売機で清涼飲料を購入するAIアルゴリズムを作ろうとする時、隕石が落ちて来たらどうしようか、自動販売機に爆弾が仕掛けられていたらどうしようか、といった様な、人間なら問題なく省略する判断を、どうやって省略させるか、という問題が非常に難しい。 |
| アルゴリズムに隕石や爆弾を回避する部分を最初から入れなければ済む話であり、問題は存在しないのではないか。 |
この点についてコメントしようと思って、私も挙手したが、時間切れで発言できなかった。
私が言おうとした事は、以下だ。
| 人間精神をフルに再現するAIを作る問題、という物を考えるとき、発表者の言った様な事が問題に成るだろう。 |
BB会場は、東北学院大学泉キャンパス2号館4階241教室だった。
19pBB-12「学問、教育とカネの問題」では、液晶プロジェクターで資料を掲示しながら、次の様に口述した。
| 発言タイミング | 発言内容 | 注釈 |
| OHP-13-1 | 宇田雄一です。 学問、教育とカネの問題について発表します。 この言い方は、政治とカネの問題という言い方の真似です。 今回の私の発表は、政治の選挙の預かり補償金の様な働きを授業料がしている、という問題についてです。 つまり、学習を抑制する働きを授業料が担っている、という問題についてです。 教育は学習を促進できるのみであって、教育が学習を抑制する口実に使われる事があっては、いけません。 しかし、現実の状況では、授業料が預かり補償金として働いており、また、その事は意図されている、と思います。 今回の発表では、どうしてこう成るのか、原因の見当を付け、解決に役立てる事を目指します。 |
政治の選挙の預かり補償金の働きは、名目上は、ひやかしでの出馬を防ぐ事だ、と思います。 名目上はそうですが、預かり補償金を置く本当の理由は選挙結果をコントロールする事だろう、と私は思う。 教育を受ける事は、普通は、純然たる消費ではなく、将来よりよく稼ぐ為の自己への投資であるから、教育を受ける権利の獲得競争(競争相手が教育を受ける権利を獲得するのを妨害する事)は、仕事の奪い合いの一形態であり、存在していそうである。 |
| OHP-13-2 | 生徒の財力による学習サポートの違いは、公道での乗り物の違いに、喩えられます。 図書館に行けば何かの本には書かれている事だ、という意味で、学問の知識はゼロ円の知識です。 それを公道に喩えます。 「おおやけのみち」の公道ですねえ。 教育はゼロ円の知識を案内するだけの学習サポートであり、これを、公道上の乗り物に喩えます。 独学は徒歩に、廉価な教育は自転車に、高価な教育は自動車に喩えられます。 これなら、おカネの無い人も、「どうしても」という場合には、才能の如何によっては、徒歩で進めば、目的地まで、たどり着く事が出来ます。 財力の大きい学習者の方が、財力の小さい学習者よりも大きな乗り物を利用できる、という不平等は、私の批判の対象ではありません。 |
私は、自分の物理学正典には解説書としてのオリジナリティーは有るが学問上のオリジナリティーは無い、と考えている。 |
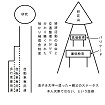
| OHP-13-3 | 実際には、(左の図を指して)この様に、歩道と自転車道が途中で行き止まりに成っている、という形で、通行止めが存在します。 乗り物の選択だけなら、貧しい学習者にも研究山にたどり着くチャンスが与えられますが、通行止めがあれば、それは不可能です。 これは、学習を促進するだけであるはずの教育という物が、実質上は、(右の図を指して)この様に、学習を阻止するバリケードの様な役割を担わされている、という事を意味します。 巷では、息子を大学へ遣った、というフレーズが、「よく経済的に一人前で有り得た」という親父の自尊心の発露として用いられる事が有ります。 これは、進路が息子やムスメの適性のみで決まらないのが実態である事の証拠だ、と見なせるでしょう。 |
|
| OHP-13-4 | 通行止めは具体的には、資格付与の条件、企業の採用基準、学問上の業績の認定において所定の教育課程を修了した事が必要とされる、という形で存在しています。 この通行止めを解除するには、資格付与の条件等で、所定の学力に達している事のみが要求される、という形に、教育機能と評価機能を分離するのが有効だ、と思われます。 そうすれば、大学は私塾や予備校と同列にまで格下げされ、形式的に要求されるレベルが下がった分だけ市場規模が拡大し、本来の健全な競争が活性化され、学生の就職先にも成ります。 ただし、実習物の扱いを、キチンと考える必要があります。 |
「格下げ」というのは、ステータス(社会的地位)が下がる、という意味であって、授業内容のレベルが私塾や予備校よりも現在の学校の方が高い、という意味ではありません。 教育・学習経済は、労働的価値観によって敵視され、その本来の市場規模よりも小さく抑圧されている、のではないか、と私は思う。 |
| OHP-13-5 | 通行止めは次の様にして維持されているのではないか、と私は疑います。 | |
| まず、研究から収入が得られない、という問題を故意に未解決のままにしておき、学者をカネに困らせます。 すると、学者は教育で収入を得る事が、どうしても必要に成ります。 こうしておけば学者は、何かにつけ所定の教育課程を修了した事が要求される、という助け舟を自ら「間違ってます」なんて言わない様に成ります。 後進育成の必要から言っても、それは助け舟です。 ただし、研究しているレベルの先生から教わりたい、という需要が存在するはずなので、生徒の都合が無視されているわけではない、と思います。 |
||
| 次に、大卒者用職種に高卒者を採用する事が陰に妨害されている疑い、があります。 | 高卒者を大卒者用職種に採用しようとすると面接回数が1回しか許されず質問内容も制限されていて採用が困難だった、という雇用者の感想をインターネットで見た。 陰謀によってそう成っているのだ、と思った。 |
|
| さらに研究については、論文のレフェリーが嘘を付ける環境に置かれている事や、論文誌は私立だから論文の採用義務を負わないのに、論文誌に掲載された論文のみが業績だ、とされる事の不条理が、挙げられます。 | ||
| 独学に対する直接的な妨害が陰に行われている事も、実感します。 学校に行かないのなら働きなさい、という強要がそれです。 |
法科大学院制度も昔ながらの浪人独学を出来にくくする目的で設置されたのではないか、と私は疑っている。 | |
| OHP-13-6 | 預かり補償金制度風の学習妨害の目的は、カネを払った人にカネが入って来る、という仕組を成立させる事だろう、と私は思います。 これは、悪意だと言わざるを得ません。 本当は、正しいのは、適性に応じて働き、働きに応じてカネが入って来る、という仕組だからです。 研究についても著作権と同様に、発見に伴う権利は発見と同時に発生する、とするのが本当は正しいはずです。 |
|
| OHP-13-7 | 学問の教育は、その本来の志向性が学者要請コースである、のに対して、企業の雇用者は学習で獲得された学力ではなく相対的優秀性を見ている、というギャップに注意して適合の良さを表にしてみました。 (左列の2つの△印を指して)これらは、就職時期が雇用者の希望よりも遅いので、△印にしました。 |
学校の成績がズッと首位だった生徒は学者に成る。 必ずそう成るとは限らないが、コンセプトとしては、そうだ。 学校教育は志向性としては学者要請コースだ、というのは、そういう意味です。 |
| 雇用者については、2つに分類してみましたが、学校の教育を全く評価しないタイプの人としては、これ、入学試験に合格する様な人材が欲しい、というタイプ。 それから、学校の教育を評価するタイプの雇用者としては、学者要請コースを経た人が欲しい、というタイプですね。 こう2つに分類しました。 学生はですねえ、これは大学教育の話なんですが、学生は3つに分類しました。 雇用者の採用基準に適合するのが目的で大学へ行く人ですねえ、そのために勉強しろと言えばするし、しなくても良いと言えばしないし、といった様なタイプですねえ。 就職するのが目的で学校に行く、という事ですねえ。 もう一つのタイプは、学習した事を仕事で役立てたいという、これはもう少し勉強を重んじる学生ですねえ。 さらに、もう一つ、これはちょっと、普通は言われない事だと思いますが、純然たる消費として講義を受ける、それだってアリですよねえ。 まあ、そういう風に分類してみました。 それでですねえ、例えば私のアイデアなんですが、入学試験に合格する人材が欲しいという雇用者は、それじゃあ、合格通知を持参すれば大卒扱いで選考する、という風にしたらどうか、という風なアイデアを思い付いたりですね、そんなとこです。 ここ長期試験と書いてあるのは、これは、中学校で言うと中間・期末試験とか、大学で言うと前期試験・後期試験みたいな物の集積の様な物ですねえ。 それを、教育機関から分離して評価機関が行った様な物というのを考えました。 |
何歳で就職するかが、雇用者と被雇用者のマッチングだけで決定されるならば、児童労働の禁止に基づく権利は保障されないので、マッチング原理よりも優先される規則として、児童労働の禁止や、それを適度に拡張した規則を置く事は妥当だと思う。 しかし、遅くまで勉強し続けたい、という希望は、本当は、そういう規則によって直接に保障されなくても、そういう希望が叶えられるのを阻止する目的で置かれた色々な要素(斥力)を取り除けば、本来は自然に叶えられる物だろう、と私は予想する。 |
|
| OHP-13-8 | 研究から収入が得られない、という問題の最も本来的な解決方法として、特許制度の拡張という物を考えてみました。 これは、あらゆる経済活動へのあらゆる貢献について、論功行賞を際限なく行なう、というアイデアです。 産学協同しろ、という意味ではありません。 実学以外や学問以外にも適用する事を考えます。 |
私の意見は、産学協同はするな、という意見でもありません。 |
| 発明家が利用した物理法則の発見者にも特許収入の一部が支払われる、とすべき。 発明家が常習的に聴いていた音楽の著作権者にも特許収入の一部が支払われる場合がある、とすべき。 SF小説家の作品中で直接言及されたり着想にヒントを与えた物理法則の発見者には作品販売の印税の一部が支払われる、とすべき。 といった様な事を考えました。 |
知財を生産しなくても、他人の研究を案内できるぐらいに広く深く理解している状態で居る、という事だけでも、社会への貢献だと考えられる。 |
|
| OHP-13-9 | まとめると、私の提案は、これら3つです。 たとえばですねえ、いま公立の学校、国立の学校が私塾のレベルに格下げされると、質が低下するんではないか、という風に思われるかもしれませんが、それは、いくら質が低下したと言っても、現在の学習塾が乱立している状況に相当するような物に成るだけだから、特にそんな致命的な問題ではない、と思います。 |
画像をクリックすると拡大画像が表示されます。
| 講演概要 |  19pBB-12 |
日本物理学会第71回年次大会(2016年)概要集 Web版ISSN2189-0803 DVD版ISSN2189-079X 3355ページ |
|||
| OHP |  OHP-13-1 |
 OHP-13-2 |
 OHP-13-3 |
 OHP-13-4 |
 OHP-13-5 |
 OHP-13-6 |
 OHP-13-7 |
 OHP-13-8 |
 OHP-13-9 |
||
2016年03月19日撮影分(領域13)@学会発表の実況@動画
質疑応答時間には、次の様な対話が生じました。
| 発言者 | 発言内容 | 注釈 |
| 1 | 社会人として生きて行く時に必要な能力っていう風に、何か有ると思うんですよね。 それを、どんな風にお考えですか。 |
|
| 宇田 | 直ぐに答える事は出来ません。 | |
| 1 | それと今の学力とは、どういう関係が有りますか。 | |
| 宇田 | 「今の学力」と言うと、学校で | |
| 1 | 今おっしゃっていた「学力主義」とか何か書いてあったんだけども、 | |
| 宇田 | ああ、はあ、はあ、はあ、ああ、なるほど。 | |
| 1 | 学力というものと、実社会で生きて行く能力っていうかと、どういう風な関係があるんですか。 | |
| 宇田 | 正の相関が有るんじゃないでしょうかねえ。 | |
| 1 | どういう関係があるんですか。 同じ物ですか、別物ですか。 |
|
| 宇田 | まあ一応、別でしょう。 | |
| 1 | だとすると、実社会で生きて行く上で必要な能力は、どこでどんな風にして身に付ければ良んでしょうか。 | |
| 宇田 | それはですねえ、たとえばですねえ、ここの表で言ってですね、入学試験に合格する様な人材が欲しい、という雇用者の場合は、それは、あの、学校に行く代わりにウチに早く入社してくれれば私が教えますよ、という、そういうタイプの人ですね、きっとねえ。 | |
| 1 | それ以外の人も沢山、あの、色んな能力が必要ですよねえ、 | |
| 宇田 | はい。 | |
| 1 | 生きて行く上では。 | |
| 宇田 | はい。 | |
| 1 | 協調性だったりとか、クリエイティブだったりとか、誠意だったりとか、真摯な思いだったりとか。 | |
| 宇田 | うん。 | |
| 1 | そういう物は、どこで身に付けるんですか、私達は。 このスキームには無い様な気がしたんで、訊いています。 |
|
| 宇田 | ふーむ、ちょっと即座には答えれませんが私は、それは現状でも学校が担い切れている物だとは思わないんですけどね。 | |
| 1 | じゃあ、どこで、それは身に付けなきゃあいけないんでしょうか、僕達は。 | |
| 宇田 | それは、あの、自然に身に付いたりとか、家庭内教育というかねえ、そういう物で身に付けたりとか、それから放課後に他人と接する間に身に付けたりとか、そういうものであって、学校が責任を持って担当する事でも今はないと思いますよ。 | 高校以上ではそうだけれど、小学校には、むしろ道徳の科学といった科目を新規追加すべきだ、と私は思っている。 その意味で、自分の意見を上手く言えていない。 |
| 1 | 教師の役割は何ですか、その時。 | |
| 宇田 | 教師の役割というのは、私そっちの専門をキチッと勉強した事が無いから分かりませんが、多分キチッと定められてると思うんですよ。 国家公務員法とか、そういう |
|
| 1 | そういう法的な問題ではなくって、人としての関わり方として、教師の役割は何ですか、って訊いたつもりです。 | 法や指導要領の中に、人としての関わり方についても、教師の役割が規範的に定められているだろう、と推測する。 |
| 宇田 | 私はねえ、知育だと思ってるんですよ。 かなり、そっちに偏った考え方を持ってます。 |
体育大学では体育の方が中心であるだろう。 そいう観点の一々を取り入れた返答は出来なかった。 |
| 1 | 有難うございます。 | |
| 2 | まあ色んな議論が必要だと思うんだけれども、おっしゃるような事、要は大学での教育費まあ授業料、これが必要でない国ってのが幾つか有ります。 で、それは実は人権条約のシイ規約って言うので、日本は批准してないから授業料取れるんだけど、批准してる国は、スペインとかそうなんですけども、そういう授業料を払わずに大学に行ける、っていうシステムに成ってます。 で、そこの国で何が起こってるか、一回見て頂いた方が良いと思います。 |
アドヴァイスに従い、帰宅後インターネットで、大学学費無料の国の現状を調べてみたが、ハッキリした事は分からなかった。 私の主張は、学費を無料にしろ、という物ではありません。 この事は発表中の口述内容の「財力の大きい学習者の方が、財力の小さい学習者よりも大きな乗り物を利用できる、という不平等は、私の批判の対象ではありません」という部分に関係します。 |
| 宇田 | 有難うございます、はい。 | |
| 座長 | あの、私からチョッと質問したいんですが、どちらかと言うと、これ、学問に関する事なのですが、通常、義務教育とか、小中高と行事がありますけれども、そういう物はどういう風に | |
| 宇田 | そういうのはですねえ、私の問題意識からすると、これで言うと、比較的誰でも選択できる、というか、この分で言うと、歩道や自転車道に相当してる物で、自動車道でないと行けない所がある所が問題という事に成ると、これは大学教育とか大学院とか、そういう物を経ないと行けない様な場所がある、という、そういう問題意識が非常に強いわけで、そういう意味で、小学校や中学校にも有る様な分野というのは、あまり問題に引っ掛かって来ない、という感じが有ります。 | 私の今回の発表内容は、現状に対する批判と改善案です。 「問題に引っ掛かって来ない」という事は、批判の対象には成らない、という事であり、そのままで良い、という事です。 つまり、学校行事を無くせ、という主張は、私の発表には含まれていません。 |
| 1 | 「どういう位置付けですか」って伺ったんですよ、あの先生は。 小中高の行事、学校行事がありますよねえ、運動会があったりとか、文化祭があったりとか。 そういう物は、どういう位置付けですか、っていう意味ですよねえ。 |
|
| 座長 | はい。 | |
| 宇田 | 位置付けって、私の議論における位置付けですよねえ。 | 私の議論においては学校行事は、「ただし、実習物の扱いを、キチンと考える必要があります」という風に言及されている部分に該当します。 |
| 1 | って言うか、まあ、人間形成における | |
| ? | そのまま取ると、その部分が欠けてしまうと、今の学校教育の根幹が見えなく成ってしまう、というか。 社会性。 |
|
| 宇田 | それを取り除け、という思想では全然ないです。 | 私の言う「学力主義」は、「学歴主義」への改善案であって、学力以外の項目を除外せよ、という主張ではありません。 |
| 1 | 人間形成にはとても重要だ、と思います。 | |
| 宇田 | そうですねえ。 | |
| 1 | 人が集まって学ぶ、っていうのは、そういう事が必要だからです。 |
教育機能と評価機能を分離すべきだ、という私の主張の適用によって学校が失うのは、実質上の卒業資格を付与する権限だけです。
私の主張は、学校は知育以外の教育機能を失うべきだ、という主張ではありません。
私の意見は、個々の学校が独自に卒業資格を発行する事を禁止すべきだ、という意見でも有りません。
評価専門の機関から発行された評価値に比べて、学校独自の卒業資格は人気を失うだろう、という意見です。
これは、英語教育において、TOEFLやTOEICが発行する評価値の方が、学校が発行する評価値よりも人気があるのと同様です。
個々の学校が、自分の発行した評価値(卒業資格も)の人気を、その評価値の有意性を高める事によって、評価専門の機関によって発行された評価値の人気よりも、高くしようと努める事は、全くその学校の自由だと思います。
語学技能や高校までの教科と違って、大学で学ばれる科目は学力テストに馴染まない、という難点が、私の今回の発表内容には有る。
私自身、学生時代、テストが勉強の邪魔に成る、と思った。
テストがあると、勉強し終わった事をいつまでも覚えておかなければいけないからだ。
しかし、試験範囲を狭く限ったテストを多数用意して、公文式みたいに(違ってたらゴメン)、都合の良い時に都合の良い人だけが受験する、という方式なら、そういう弊害も生じないのではないか。
大学レベルでは、単位取得の要件としてテストで一定以上の成績を上げる事を課すよりも、既に実際そうである様に、レポートの提出を課す方が、学ばれる内容に良く馴染む、と思う。
研究して論文を執筆する、という段階の前段階だからだろう。
評価機関にレポートを提出する、という形式が良さそうだが、他人の書いた物を丸写しして提出する、という不正を防ぐ力を強化する問題が残される。
学力主義という事に成ると、実習物の教育効果が無視されてしまい、これでは完全ではありません。
学力の方はどういう過程を修了したかを、学力の直接測定で置き換える事が出来ますが、実習物については、どういう課程を修了したか、という基準で量るしかない、かもしれない。
しかし、原理的には、学校で育てられている属性の全てを学力だ、と定義して、学歴主義ではなく学力主義を、という風に言えば、間違いが減ると思う。
私が言う学力主義は、そういう意味であって、例えば体力は評価されない、という事を言う物ではない。
誰からの授業を何時間受けたか、何を何時間練習したか、そういう基準でではなく、結果として何が出来る様になったか、で評価しよう、という考え方です。
私の主張は「学歴主義ではなく学力主義を」という物であり、これを「学力主義を」という風に要約してしまうと、非常に誤解を招き易い、と思う。
教育の中心は知育だと思う、という私の態度は、発表中には「学問の教育は、その本来の志向性が学者要請コースである」という言葉で、述べられています。
そして、学校とは本来、学問の校だから学校なのだ、と私は思っている。
現在では他の要素も有るけれど、元々はそうであったはずだ。
そして、現在でも、それが根幹であるはずだ。
昔の日本には、女だからという理由で、女子を学校に通わせ渋った親が多かった、という話を聞いた事がある。
そういう親の決まり文句は「女に学問は必要ない」だった、と聞く。
これは、学校は学問の校だ、と考えられていた事の証拠だろう。
学校という意味の英単語「school」と学問という意味の英単語「scholarship」の語幹が同じである事も、その事を裏付ける。
知育と徳育は別だが、何を通して徳育するか、という事に関しては、知育だけが除外されるのも、おかしい。
学校行事だって徳育とは別である。
学校行事を通しての徳育が考えられるなら、当然、知育を通しての徳育だって考えられ、学校という物が始まったばかりの頃は、おそらく、知育を通しての徳育、という考え方が言われていたはずだ。
学問においては、才能についてだけでなく、勤勉さや誠実さといった徳育の対象と成る様な性質について、ボロが出やすい。
だから、知育を通して徳育する、という方式は、なかなか当たっているのではないか。
道徳の科学といった科目を置けば、それは、知育を通しての徳育といった間接的な物ではなく、知育でありながら直接的な徳育でもある。
この様に、徳育は大きく知育に頼る物であり、知育重視=徳育軽視と考えるのは間違いだと思う。
預かり補償金という観点からだけだと、確かに、学費が無料ならば、批判の余地は有りません。
しかし、もし仮に全ての学校の学費が無料であっても、誰かから学問を習わなければ何を発見しても発見したとは認定されない、という事が有ってはいけないのは当然の事です。
そういう批判の意味も私は今回の発表に込めたつもりですが、この点を言えてない事は、冒頭での私の「今回の私の発表は、政治の選挙の預かり補償金の様な働きを授業料がしている、という問題についてです」という宣言の、不完全な所です。
また学費が無料でも、入学試験に合格しなければ自分のやりたい分野を勉強してはいけない、という風に成っているとしたら、それは変です。
独学が実質上禁止されるなら、そういう事に成ってしまいます。
徳育については、学校という物は、新しい人材を送り込む事によって社会の現状の悪い習慣を改善して行く、という役割を担っていると思う。
次の代からはチャンとやろう、という風にです。
道徳は社会人に成ってから社会から教えてもらえ、という方式では、それが出来ない。
そういう意味で、社会で実際に通用してしまっているルールよりは、学校的なルールの方が好ましい、と感じる傾向が私にはある。
こういう点についても、発表会場では上手く言えなかった。
最近では、学校でもイジメの問題が深刻化していて、学校的なルールという物も今では良く分からなく成って来ている。
これは、学校が大人の社会みたいに成って来ている事、悪い習慣の低年齢化、とも言える現象ではないか。
逆に、コンプライアンスの行き過ぎで不具合が生じている、という問題が最近の実社会には生じているらしいが、これは学校的な秩序を社会に持ち込み過ぎた事の弊害ではないか、という風な疑い方も私はしている。
社会の学校化が無制限に善であるわけでもない、と思う。