
since 2003
イレコナビ サイトマップ
日本物理学会2015年秋季大会での私の発表は、文法物理学についての25pSC-2「宇田方程式の離散解にダルマ落とし公式を適用」および物理教育についての17pAL-10「ソレダケノモンの数理(3)」の2つだった。
発表旅行中に撮影された写真は、私の写メール投稿ブログ「即達」の2015年09月分のページに掲載されています。
AL会場は、関西大学千里山キャンパス第2学舎2号館5階C507教室だった。
17pAL-10「ソレダケノモンの数理(3)」では、液晶プロジェクターで資料を掲示しながら、次の様に口述した。
| 発言タイミング | 発言内容 | 注釈 |
| OHP-13-1 | 今回は、2015年春の大会で発表した先生、教育種目、生徒の相互選択アルゴリズム、に付け足すべき条件を発表します。 前回の発表では私は、先生全員と生徒全員の間に1対1対応を付けるアルゴリズム、を発表しました。 しかし、このアルゴリズムを現実の問題に応用するには、そのままではダメで、 |
左記発言の開始は、2015年09月17日16時01分19秒頃です。 |
| OHP-13-2 | これらの問題への解決法、を加味する必要があります。 [(1)を指して]現実の問題では、先生も生徒も必ず誰かを選ぶ、というわけではなく、ある程度までなら妥協するけど、それ以上の妥協が必要なら誰とも組まない、という選択が有り得ます。 この状況は、先生と生徒の志望序列表にno oneが含まれる場合、として定式化出来るでしょう。 [(2)を指して]前回の発表では、各クラスの定員が1人の場合について、しか述べませんでした。 また、定員の合計が生徒候補の人数と一致しない場合についても、前回は述べませんでした。 [(3)を指して]前回の発表では、無償の自由教育のみを論じました。 有償教育の場合、教育を受ける権利を保障するための奨学金を割り出す問題、が自明ではなさそうです。 [(4)を指して]特定の教育種目の履修者数が社会全体で最低でも何人は必要だ、という文化保存等の公の都合が存在する場合はどうするのか、という問題も有ります。 保護されるべき公益の候補としては、全体の価値は個の価値の単純和を超える、という価値観に基づく全体の価値も考えられます。 つまり、そういう価値観に基づいて個人の自由に制限を課す事の限界も、私の原理から定まるでしょう。 [(5)を指して]これは、物理と化学を選択するか生物と地学を選択するか、どちらの方がマシだと生徒が思っているか、という意味での志望序列が存在する場合の事です。 1つだけ選べと言われた場合の第1志望が物理、第2志望が生物、第3志望が化学であっても、2つだけ選べと言われた場合には生徒は、上から2つ取った物理と生物を選ぶよりも、物理と化学を選ぶ方がマシだ、と思うかもしれません。 [(6)を指して]志望がバラけた場合対応が不定に成る事、を前回発表しましたが、この場合にはどう決めれば良いのかは、まだ考えていません。 [(4)を指して]今回は特に、(4)について、詳しく述べます。 |
|
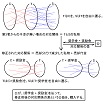
| OHP-13-3 | (最上段右端の文を指して)行政の介入が無い場合の契約内容は当事者の私物だ、という認識に基づいて、これに対して行政が変更を要請し、その変更に対して税金で報酬を支払う、という形で行政が私物を税金で購入する、という描像を用いて、この問題を分析してみます。 その購入の具体的な形としては、保存されるべき種目の先生には、生徒から受け取る授業料とは別に、行政から奨励金が支払われる、保存されるべき種目の生徒は授業料の一部を行政から代わりに払ってもらえる、という前提の下で生徒と先生が有償教育の場合のルールに基づいた自由選択を行なう、という形式を考えます。 これは、奨学金や奨励金という言葉に対する普通の用語法とは違うかもしれませんが、そういう風に言う事にします。 公務員である公立学校の先生に税金から支払われる給料も、私の用語法では、奨学金や奨励金です。 奨学金の額が授業料の額よりも大きい場合には、超過分は生徒への給与だと考えられ、そういうケースは、防衛大学や警察学校に、見られます。 民間の奨学金については、まだ考えていません。 (最上段の図を指して)ええ、これ上段の図ですが、まず、第三者からの干渉なしで、先生が教育種目を、生徒が先生を自由に選んだ結果得られる対応関係は、各々の先生と生徒の私物の並存状態だ、と考えます。 これは、自由な相互選択の結果は、誰から奪った物でもなく、当事者が元から外部に持っている自分だ、という考え方です。 (下段の図を指して)行政から、保存種目には奨学金と奨励金を払います、という干渉がある場合には、先生は教育種目プラス奨励金を、生徒は先生プラス奨学金を自由に選びます。 (中段の「公」の図を指して)上の対応関係から下の対応関係へ移行する事は、公が奨学金と奨励金を払って対応関係の差という公益を購入した、 (下向きの矢印↓を指して)生徒と先生は私物の一部を公に売却してその代金として奨学金や奨励金を得た、という風に理解されます。 (下向きの矢印↓の下端の式を指して)売却後は、先生と生徒の手元には、代金と売却分だけ減少した私物が残っている、という状態に成り、これが下の図の対応関係です。 |
|
| OHP-13-4 | (1行目の式を指して)自由に選ぶ、と言っても、自由に選べるのは自分の志望序列表の内容だけであり、前回の発表から示唆される様に、先生の志望序列表の内容と生徒の志望序列表の内容から、対応関係は決まってしまうので、 (最も右の下向き矢印↓を指して)公の介入による対応関係の変化は、(最も左の下向き矢印↓を指して)先生と(真ん中の下向き矢印↓を指して)生徒の志望序列表の内容の変化を通してのみ、生じるのであって、対応関係を直接選ぶ事は出来ません。 |
|
|
(最も左の右向き矢印→を指して)奨学金や奨励金が有る場合には、その金額が先生や生徒に参照される事によって、生徒と先生の志望状況が奨学金と奨励金の関数として変化します。 (真ん中の右向き矢印→を指して)志望状況から対応関係が決まる事は、先に述べた通りです。 (最も右の右向き矢印→を指して)また、各種目の履修者数は、対応関係の関数です。 したがって、各種目の履修者数は、奨学金と奨励金の関数と見なせます。 これは、種目別に言える事ではなくて、全体としての話です。 つまり、奨学金と奨励金を保存種目全体にどう配分するか決めれば、各々の保存種目の履修者数が決まる、という事であって、一つの種目の奨学金と奨励金の額がその種目の履修者数を決める、という事ではありません。 |
||
|
(結末の文を指して)そこで、全ての保存種目の履修者数が必要最小値に成る様な奨学金と奨励金の配分、という物が、その関数関係から決まるはずで、そういう配分が正義に叶っている、と考えられます。 全体としては、それが高いという事は、譲るのがそれだけ嫌だ、という事であり、高くて納税への同意が得られにくいからと言って値切ろうとする事は、その分無償で譲歩しようとする態度だから、これは、譲歩するのが納税と同じぐらい嫌である事に矛盾します。 つまり、その額が如何に高額であろうとも、それがその値段なのです。 高くて納税への同意が得られない事は、公の意志が保存を支持していない事とイクオールです。 ここまでが、税方式の説明です。 |
||
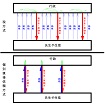
| OHP-13-5 | ここから、個別に「あなた、譲りなさい」といって要請する方法が、税方式に比べて、どう間違っているのか、を説明します。 | |
|
(税方式の段を指して)税方式でも全体としては、払った分だけ受け取るのであり、奨学金と奨励金が無から湧いて出て来て譲歩負担の埋め合わせをしてくれる、という事はありません。 志望変更したい人の志望変更という形での負担は奨学金や奨励金で相殺されますが、そういう人も含めて全員に納税という形での負担が掛かります。 |
||
|
(個別依頼方式の段を指して)個別依頼方式は、これを税方式に換算すると、譲歩する人が自分で自分に奨学金や奨励金を払う事に相当します。 譲歩を依頼された人にとっては、自分の正直な主観での譲歩分相当の奨学金や奨励金の金額だけ納税し、何も譲歩しないのと同じです。 つまり、これは、公定額、公的に定められた金額、という意味ですね。 つまり、これは、公定額に基づかず私人間の交渉の形式で個別に徴税して回る、みたいな物であり、ほとんど私有財産の否定です。 税負担の不公平に相当する不公平を生みます。 |
||
| OHP-13-6 | 結局、(「負担量」の段の左端を指して)負担量の問題、(「意志・納得」の段の左端を指して)意志・納得の問題、(「必要性の検証」の段の左端を指して)必要性の検証の問題、の3つが有ります。 | ※のタイミングで、何か声(私以外の)の様な音が聞こえる。 左記発言の終了は、2015年09月17日16時13分23秒頃です。 |
|
個別依頼方式の場合には、(最も左上の長方形の枠内を指して) (1件あたりの譲歩分相当の金額)×(志望を変更する人数) が、 税方式の場合には、(最も右上の長方形の枠内を指して) (1人あたりの納税額)×(納税者数) が、 負担量の合計ですが、税方式の場合には、最小化原理が有るから(上端の語を指した)、志望変更の負担を軽いと感じる人から順に志望変更するのに対して、個別依頼方式では、そういう調整機能が無いので、両者は等しく成らず、後者の方が小さく成ります。(最も上の不等号>を指した) また、保存種目は非常に少ないので、自分の志望序列表の内容を変更する人の人数は、納税者の人数よりも遥かに小さい、と考えられます。(負担量の段の不等号<<を指した) (負担量の段の不等号>>を指して)従って、(1件あたりの譲歩分相当の金額)は(1人当たりの納税額)よりも遥かに大きい事に成ります。 つまり、個別依頼方式は特定少数の人に全部負担してもらう方式(負担量の段の左下の長方形枠を指した)であり、税方式はみんなで少しづつ負担する方式(負担量の段の右下の長方形枠を指した)だ、と言えます。 |
||
|
(「快く応じた人」のセルを指して)個別依頼方式では、快く応じた人は、任意の意志で高額寄付をしたのと同じであり、それが本当に任意の意志であったなら、問題は無いのですが、嫌だが断れなかった人が、高額の負担を押し付けられたのと同じ目に遭ってしまい(「嫌だが断れなかった人」のセルを指して)、この点が問題です。 税方式では、各人には、私は払いません、といって任意に拒否する権利は無いけれど、税の導入に反対の一票を投じる機会は与えられています。 税方式でも、税の導入に反対した人は(「税の導入に反対した人」のセルを指して)、意に反して負担を押し付けられるわけですが、それは少額だし、そういう人が過半数なら、その税は導入されないので、そういう人は半数未満です。 税の導入に賛成した人は(「税の導入に賛成した人」のセルを指して)、任意の意志で少額の寄付をしたのと同じであり、税方式では、そういう人が過半数です。 |
||
|
(「必要性の検証」の段を指して)高過ぎるから払いたくない、という意見が趨勢である事が、保存の必要が公的に認められない事の、定義であるし、それで済むなら安いもんだ、という意見が趨勢である事が、保存の必要が公的に認められる事の、定義に他ならないので、税方式では選挙によって保存の必要性が検証されます。 そして、実際の選挙で少しでも増税を口にすると著しく不利に成る事を見れば分かる様に、この検証は非常に厳しく、公的保護の対象と成る種目は例外中の例外と言えるぐらいにまで厳選される、と考えられます。 ついでの話、公の都合ですらそうなのだから、息子には父の職業の後を継いでほしい、という私的な都合が個人の自由に課す事が出来る制限は皆無だ、と考えられます。※ 個別依頼方式では、各種目の保存の必要性が投票によって検証されないので、依頼する人の判断が甘く成るし、依頼された人が、保存が必要だとみんなが思ってるんですよ、という風に言われた場合に、もしそれが嘘や間違いであっても、嘘や間違いだと見破る事が難しく、ましてや、嘘や間違いである事を相手に認めさせる事は、ほとんど不可能です。 この事は、(「必要性の検証」の段内から「意志・納得」の段内まで引かれた矢印を指して)嫌だから断りたい人が義務の無い事を断れなく成ってしまう危険、を増大させます。 最小化が為されない分に加えて、その分も、全体として税方式の場合よりも負担の合計が大きく成るでしょう。 個別依頼方式では、依頼された人の「なぜ私が」という疑問に対して、他の人にも他の事で譲歩をお願いしているんですよ、という説明が考えられますが、そんなのは幾らでも嘘が吐けるし、そういう分担が誠実に行われていたとしても、公的に定めるの公定ですねえ、公定、定量化されていないので、到底公平には成り得ません。 過半数の人が足並みを揃えて判断を誤る事だってあるので、選挙による検証は完全ではないし、選挙で尋ねられるのは負担の是非であって必要性そのものではありません。 しかし、選挙に基づくならば、判断を誤っても、おおよそは誤った人が報いを受けるのだし、誰かが負担しなければいけない、という意見の是非は検証されます。 必要ではない、という結論が出ていなくても、必要だが負担は無理だ、という結論が出ているだけでも、断る理由として十分です。 むしろ、そういう投票結果の方が、負担条件抜きで必要だと思うか否かを尋ねたアンケート結果よりも、意味のあるデータだと言えます。 個別依頼方式でも必要性が全く検証されないわけではなく、依頼者と被依頼者の話し合いに検証作用が有りますが、断るためには討論に勝たなければいけない、という要素が少しでも有れば、それは断る権利の否定であり、容認できません。 |
||
| 会場では発言されなかった部分 | 結局、個別依頼方式は、嫌だが断れなかった人が大きな損害を受ける点で、悪意が存在しない場合でも小さくない間違いが起こり、悪用されれば実質上の強盗を可能にしてしまうので、危険です。 どんなに大金を積まれても断る、というタイプの人は、税方式なら断れますが、個別依頼方式では押し付けられてしまう可能性があり、個別依頼方式の悪用においては、特にそういう人が目の敵にされて狙われる事が懸念されます。 私を雇っている人でも私と同じ雇用者に雇われている人でもない人から、ただ私が近くに居て手が空いている、という理由だけで、なぜ手伝わないんだ、という風に責められ、驚き呆れた経験が私にはあります。 |
時間切れで音読できませんでした。 どんなに大金を積まれても断る、というタイプの人は、単なる好みの場合もあるでしょうけれど、志望変更しない場合の第1志望に進んだ場合の将来性が非常に大きいからそうなのだ、という事は有りがちです。 その将来性が目の敵にされ、失わせようと付け狙われる恐れがあります。 宇田経済学@持論 |
| 税方式でも、オカネを持っている人がオカネを持っていない人に譲らせる作用、が問題に成り得ます。 これが問題であるか否かは、前提として存在している経済システムの如何によって、変わります。 現行の経済システムでは、問題だと思います。 その点への改善を含む経済理論を私は目下考案中です。 それを私は、宇田英才教室サイト内に宇田経済学として書き進めています。 オカネを持っている人がオカネを持っていない人に譲らせる事の全てが不条理なわけではない事は、例えば大学で奨学金を貰ったので大学院では奨学金を貰う必要が無く成った、という場合を考えれば、鮮明に分かります。 この場合、その人は、既にオカネを持っているという理由で、オカネが足りなくて大学院で奨学金を貰う人に進路を譲らせている、と考えられますが、既に持っているオカネというのが進路を譲った事によって得た物だから、譲り合いで問題なし、と考えられるからです。 税方式でも、不正工作によって被害者をカネに困らせる事によって奨学金目当てに自分で譲る様に仕向ける、という手口によれば、個別依頼方式を悪用した実質上の強盗と同じ結果を狙う事が出来ますが、これは税方式の欠点ではなく、不正工作防止の問題でしょう。 |
||
| 特定種目の保存が公的に選択された、という事は、それに要する額の納税をしてもよい、という納得が選挙を通して得られた、という事です。 この条件は非常に厳しいのに対して、個別に譲歩を要請すると、増税公約で選挙に勝たなくてもよいので譲らせ過ぎが起こるし、税負担の不公平に相当する不公平も生じます。 |
画像をクリックすると拡大画像が表示されます。
| 講演概要 |  17pAL-10 |
日本物理学会2015年秋季大会 概要集 Web版 ISSN 2189-0803 DVD版 ISSN 2189-079X 3060ページより。 |
||||
| OHP |  OHP-13-1 |
 OHP-13-2 |
 OHP-13-3 |
 OHP-13-4 |
 OHP-13-5 |
 OHP-13-6 |
2015年09月17日撮影分@学会発表の実況@動画
質疑応答時間には、次の様な対話が生じました。
| 発言者 | 発言内容 | 注釈 |
| 1 | たぶん、今日のお話は社会物理的な側面が強いのかなあ、と思って、お聞きしてたんですけど、このモデルに対して、どうやって検証されます? 仮説としては、何か、面白そうには思えるんですけども、物理だったら、やっぱり検証しないといけないんだ、と思うんですね。 その検証は、どうされますか? |
|
| 宇田 | 検証というのは、あの、どの点を検証すんでしょうか? | |
| 1 | いや、こういう今日のお話全体のモデルとした時に、それがモデルが正しいかどうかを検証と言うんでしょう。 | |
| 宇田 | 正しいかどうか? | |
| 1 | うん。 | |
| 宇田 | あの、何が、 あ、そうか、そうか、何が どういう結果が得られれば、正しいと言えるか、訊こうと思ったんだけど、それが無いでしょう、という話ですね? |
|
| 1 | どうやれば、これが、今の話が検証できるか分からないな、って思って、聞いてたんですけど。 | |
| 宇田 | これは、だけど、私の場合、これはですねえ、主義主張ですから、「みんな民主主義で行こうよ、ねえ、それが正しいよね」と言ってるのと同じなんですよ。 そういう意見に対して、どうやったら検証できますか、という批判と同じだと思いますねえ、今の御批判はねえ。 まあ、質問ですか、質問かもしれないけれど。 うん、これ、私の価値観と言うかねえ、その様な物で、こういうのが正しいでしょう、という事で、根源的な物ですから、それに照らして、これは矛盾ですよね、とかね、そういう物は言えると思いますけれど、それ自体が正しいかどうか、というのは、それは、調べようが無い事です。 |
価値観という言葉に対してススリ笑い反応が生じた。 私が物理学の理論を発表しているつもりだ、と思ったからだろう。 民主主義以外の例としては、資本主義や共産主義が挙げられる。 これらについて、広い意味での検証という物を考える事は出来るだろうけれど、それは、現実の現象を記述する理論として正しいか否かを検証する、という意味での検証ではなく、究極的には、それに従う事が好まれるか嫌がられるか、それに従った結果は好まれるか嫌がられるか、という形での検証だ。 |
| 2(座長) | タイトル、ソレダケノモン、というのは、何がソレダケノモンなんですか? | |
| 宇田 | あ、これはですね、もう3に成ってますよねえ、数理にしてもねえ。 ソレダケノモンの数理、数理というのが付かないのが、まず有りましてね、ソレダケノモン教育というんで、まず発表してます。 で、そこで、 ソレダケノモンという単語については、そこで説明してあるんですけれど。 掻い摘んで申し上げますと、ちょっと、もう時間来てますが、こういう話をしましたね。 これは、会話のパロディーみたいに言いますが、 「結果が出なかったじゃないか、どうしてくれるんだ」 「いや、そりゃあ、あんたが、ソレダケノモンだった、っていう事じゃあないのかい」 というのが1つですね。 で、もう1つは、 「こんなにもらっちゃって、いいのかな、と思って」というのに対して、 「もちろんですとも、旦那が、ソレダケノモンだって事なんですから」という、 まあ、良い意味と悪い意味、2つ有りますが、そういう種類のソレダケノモンという事ですねえ。 |
この辺りでススリ笑いが聞こえ、受けてる事が分かる。 大阪弁の「なんぼのもんやねん」を引き合いに出して説明したかった所だ。 発表会場が大阪だったので特に、そう言える。 なーんだ、また自己責任か、宇田のソレダケノモン概念は自己責任概念の言い換えに過ぎない、という批判は当たっていません。 私のソレダケノモン主義は、他者の助けを借りるな、という内容を含むものではなく、助ける事や助けられる事を強要するな、という内容や、誰が誰にどれだけ助けられたかの事実を歪めるな、という内容を含む物であり、直接には、授受ゼロ(助けも助けられもしない)のラインを定める物です。 何でも自己責任でやれ、という主張が正当に成る様な前提条件を成立させろ、という主張が私のソレダケノモン主義だ、とは言えるかもしれない。 ここで言う「助ける」の概念には、基本としては、犯罪への対処を助ける、という内容は含まれない。 私のソレダケノモン主義思想は、今回の話に限って言えば、OHP-13-3を掲示している時に口述した「自由な相互選択の結果は、誰から奪った物でもなく、当事者が元から外部に持っている自分だ」という思想です。 ソレダケノモン方式コーチングは、日本物理学会2014年春季大会で、発表されました。 ソレダケノモンの数理(1)は、日本物理学会2014年秋季大会で、発表されました。 ソレダケノモンの数理(2)は、日本物理学会2015年春季大会で、発表されました。 |
| ? | それって物理なんですか? | |
| 宇田 | これは、物理教育だから、物理じゃなくて、どちらかと言うと、物理教育の教育の方の話ですね。 教育一般ですね。 教育一般についての話だから、物理教育についても適用できるでしょう、という話です。 先ほど社会物理だと思いますけど、とおっしゃいまして、私は、一切反論しませんでしたが、正確に言うと、社会物理の物理の部分は付かないです。 どちらかと言うと、物理よりは経済に関係が有ります、オカネの話も出て来ましたが。 |
物理教育よりも適用範囲が広い教育理論は、物理教育の部品として使う事が出来る。 ソレダケノモン主義の経済学として目下、私は宇田経済学という物を構想中です。 |
| 2 | そうですか? | |
| 宇田 | はい、そうです。 | |
| 2 | 分かりました。 | |
| 宇田 | はい。 |
SC会場は、大阪市立大学杉本キャンパス共通教育棟1階811教室だった。
25pSC-2「宇田方程式の離散解にダルマ落とし公式を適用」では、液晶プロジェクターで資料を掲示しながら、次の様に口述した。
| 発言タイミング | 発言内容 | 注釈 |
| OHP-sr-1 | 今回は、2013年秋に私が発表したダルマ落とし確率公式を、2015年春に私が発表した疑似解に適用してみます。 今疑似解と言ったのは、解き方が定性的だったので近似解ではなかったからです。 今回の発表は、私の新理論から観測に掛かる予言を引き出す作業への着手と見なせます。 |
左記発言の開始は、2015年09月25日13時47分09秒頃です。 日本物理学会2013年秋季大会 日本物理学会2015年春季大会 |
| OHP-sr-2 | まず、私の新文法では、(最上段の図式を指して)旧来量子状態の時間発展と考えられて来た物を、(初出のΦを指して)この様な汎関数で表します。 これは、1つの時刻に1つの変数が割り当てられている様な多変数関数としてイメージされる汎関数です。 これ多変数関数を書いてます。 (「本当は汎関数」という文を指して)ホントは汎関数なんですが、(初出のΦを指して)離散化描像を、ここに書いております。 関数から汎関数に表現空間を広げた事により、旧文法の量子状態の時間発展という概念では言い表せない何事かが、私の新文法には入って来ます。 それらをひっくるめて、この汎関数で表される物を量子歴史と呼ぶ事にしました。(「量子歴史」という語を指した) これは、2005年秋に私が発表したアイデアです。 (下から2行目の記録を指して)まあ、大体こう、2005年、こう、奇遇にも、ここだったんですね。 これが私の新文法の出発点でした、発表としては。 その翌年に、(最も下に書かれている記録を指して)こう、ハワイでも発表しておりますが。 |
日本物理学会2005年秋季大会 日米合同物理学会2006年秋季大会 |
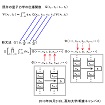
| OHP-sr-3 | 2013年秋に私が発表したダルマ落とし確率公式は、旧文法版量子力学の伝播関数に相当する関数が、私の新理論では、これである(G'を指した)、という内容を持つ物でした。 これは、どういう関数か、と言いますと、1つの量子歴史の汎関数に異なるダルマ落とし操作を加えて得られる2つの汎関数の内積として定義される関数です。 (G'の定義式の右辺を指して)ここが、まあ、内積に成ってる、という事ですねえ。 ダルマ落とし操作の内容を見てみますと、この様に、(左のダルマ落とし図を指して)変数の1つに定数を代入して、変数列からその部分をダルマ落としの要領で抜き取る、という描像で理解される物でした。 この際、ダルマ落としにおけるのと同様に、繰り下がって来た変数の番号は、1つずつズレます。 (最も右の上向きの赤色矢印↑を指して)ここの部分とか、それから、(最も右の下向きの赤色矢印↓を指して)ここの部分ですねえ。 代入する定数は、旧文法版量子力学の伝播関数の位置変数の値です。 (G'の変数のaを指して)これと、それから、(G'の変数のbを指して)これですねえ。 代入される変数の位置は、旧文法版量子力学の伝播関数の時間変数の値×αで決まります。 (左のダルマ落とし図の上脇のxqを指して)ここの位置と、それから、 (右のダルマ落とし図の上のxpを指して)ここの位置に、代入されてます。 |
最下行の発表記録に言及するのを忘れた。 |
| OHP-sr-4 | 2015年春に私が発表した疑似解は、具体的な事を切り捨てて言うと、こういう形をしていました。 (Φ[χ]=・・・の式を指して)こんな形ですねえ。 つまり、隣り合う1組の変数のみがエンタングルしている様な量子歴史の重ね合わせ、です。 まあ、ちょっと、これを簡略化して図式的に、(Φ[χ]=・・・の式の直下の図式を指して)この様に書いておきます。 これを発表したのは、この2015年3月22日早稲田大学早稲田キャンパスです。 この関数を、前のページで提示した、(最上段の積分イメージを指して)この積分に代入して計算すると、 |
|
| OHP-sr-6 | (冒頭の式を指して)こういう結果が得られます。 ただし、定数Aと関数fは、こういう風に定義されます。 (Aの式を指して)定数Aと(fの式を指して)関数fですねえ。 Aの値もfの関数形も、pとqが十分に離れていれば。 そんなに離れてなくても、2つほど離れてれば、もう良いんですが、あんまり重なってると駄目なんですが。 十分に離れていれば、pにもqにも依存しない事が、定義から言えます。 Aの値も、fの関数形も、pとqに依存しません。 G'が(G'の変数のp/αを指して)t=p/αで(G'の変数のaを指して)x=aに局在していた粒子の(G'の変数のq/αを指して)t=q/αでの波動関数の(G'の変数のbを指して)x=bでの値である事を考えると。 正確には、旧文法版ではそうであった物の代替物、という事ですねえ。 そうである事を考えると、pとqへの依存性が皆無である事は、G'が伝播関数として正しくない事を意味します。 これは、疑似解に含まれるエンタングルメントが厳密解に含まれるエンタングルメントに比べて少な過ぎるからだ、と思われます。 (冒頭の式を指して)この式の導出は、 |
|
| OHP-sr-4 | 大体、次の様に行ないます。 まず、分かり易い様に、求めたい積分の被積分関数を、この様に、図解しておきます。 (下段の図を指して)こうですねえ。 前半の因子において、(Φの式の右辺のxkを指して)ここにbを代入した物が、(下段の図中の左の因子の下から2番目の図を指して)これですねえ、この図ですねえ。 で、(Φの式の右辺のxk+1を指して)ここにbを代入した物が、(下段の図中の左の因子の上から2番目の図を指して)この図ですねえ。 その他は、(下段の図中の左の因子の最も上の図を指して)これとか、(下段の図中の左の因子の最も下の図を指して)これです。 この様な記号で、表します。 それ以外の項は、そう成ってて(独り言) 後半の因子についても、同様です。 (下段の図中の右の因子を指して)後半の因子、こっちですねえ。 こっちはbの代入ではなくて、aの代入ですが。 |
|
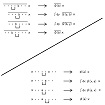
| OHP-sr-5 | (左上のエリアを指して)すると、分配の法則の適用において、前半の因子からどの項を取るかに応じた積分結果への寄与は、この様に成ります。 後半の因子からどの項を取るかに応じた積分結果への寄与は、(右下のエリアを指して)この様に成ります。 こっちの右下の半分ですねえ。 これらが、 |
|
| OHP-sr-6 | (冒頭の式を指して)この式の中の各項の由来です。 | 左記発言の終了は、2015年09月25日13時52分51秒頃です。 |
画像をクリックすると拡大画像が表示されます。
| 講演概要 |  25pSC-2 |
日本物理学会2015年秋季大会 概要集 Web版 ISSN 2189-0803 DVD版 ISSN 2189-079X 8ページより。 |
||||
| OHP |  OHP-sr-1 |
 OHP-sr-2 |
 OHP-sr-3 |
 OHP-sr-4 |
 OHP-sr-5 |
 OHP-sr-6 |
2015年09月25日撮影分@学会発表の実況@動画
この発表の原型はwww.GrammaticalPhysics.ac > Forum > Problems > Theory of Quantum History Entangled in Time-like Direction > Application of the Stacked Daruma Game Formulaです。
質疑応答時間には、次の様な対話が生じました。
| 発言者 | 発言内容 | 注釈 |
| 鈴木 | シグマがありますけれど、 | |
| 宇田 | シグマ?はい。 出しましょう。 |
|
| 鈴木 | テンソル、じゃあないですよねえ? | |
| 宇田 | 高校数学で出て来るシグマです。 和の無、ああ無限とは限らない、まあ、ここでは無限ですが、和の記号ですねえ。 |
|
| 鈴木 | 例えばね、テンソルの和には、結局、次元を考えなくて、数学的に自由に計算できる、という意味が、有りますよねえ? | |
| 宇田 | そうでしたっけー? 次元を考えなくて良いですか? |
|
| 鈴木 | それは、じゃあ、物理学的に言うと、どういう意味が有るんですか? | |
| 宇田 | 物理学的に言うと、それは、あのう、途中計算の個々の部分が、どういう物理的な概念ないし状況に対応してるか、というのは一々は分かりません。 っと、こうやって考えてみると、これ何でしょうねえ? うーん、分かりませんねえ。 分かりません、うーん。 いや、それは良い問題ですねえ。 考えてみると何か実りの有る結果が、出て来るかもしれません。 |
|
| 鈴木 | いやあ、ちょっと、何か、無意味な様な気がするんですけど。 何の為に、そういう、非常に労力の掛かる計算をね、やられておられるのか、それをちょっと心配したわけです。 |
|
| 宇田 | ああ、そうですか、無意味ではない、と思います。 旧文法版の量子力学で、時間発展というのが有ります。 ある時刻にこの位置に在った物が、別の時刻に測定すると、この位置に在る確率が幾ら幾らです、というのが有りますよねえ? それが、私の理論を使って計算すると、違うんじゃないか、という見込みなんです。 それを、出してみよう、という。 まあ、ここでは、まだ出てませんが、次回もまたそれを目指して、出るかもしれないし、という事で、しばらくそれを狙って、今回はその第1回目という事なんですよね。 まだ結果は出てませんが。 で、違うのが出れば、そうすると、実験結果で見て、宇田の方が正しいのか、旧文法版の量子力学の方が正しいのか、 まあ、私の方が正しくて、旧文法版のとズレてる、と言っても、旧文法版が間違ってる、という言い方は正しくないですが。 そういう、あのう、計算 |
|
| 鈴木 | まあ頑張ってください。 | |
| 宇田 | はいー。 意味は有ります、非常に。 |
AL会場で、最前列は次の講演者の準備の為のスペースとして空けておく必要があるか、座長に尋ねると、そんな規則はありません、と言われた。
最前列は次の講演者の準備の為のスペースとして空けておく必要がある、という規則は、前々回の大会頃に私の耳に入り、2015年春季大会のCK会場では私の自分の発表のデジカメ撮影を阻止する目的で使用された。
2015年春季大会のCK会場ではセッション開始前に、私が「(次の講演者の準備スペースを避けて)それでは空いてるここにデジカメを置くのは構いませんか?」という意味の質問をすると、座長が「他者が当たってデジカメが床に落ちて壊れても構わなければそうしてください」という暴力団まがいの脅迫的返答をした。
その位置で他者が当たる恐れは感じなかったので、協力者が故意に当たって落とすぞ、という脅迫だ、と思った。
2015年春季大会のCK会場では、最前列の中で次の講演者の準備用スペースの反対側の机は頒布物で埋められていた。
2015年春季大会のDG会場では、CK会場と比較してのみならず、過去の他の会場と比べても、撮影妨害が皆無だったのは、私の発表内容を「どーせ、公開しても、自分が恥をかくだけだ」という風に、犯人連の当該部署が高をくくっていたためで、DG会場での私の発表内容がその予想に反していたために、一転してCK会場では逆の現象が出ているのではないか、という風にCK会場での私は思った。
2015年秋の今回、私のデジカメ撮影への妨害がピタッと止んだのは、前回の発表の報告動画で再現映像という手法を初めて用いたからだ、と思われる。
この方法なら、実況動画を撮影できなくても、それ以上に分かり易い報告動画を公開できる。
2011年秋に初めて撮影公開した時には皆無だった撮影妨害が2015年春までは徐々にエスカレートしていた。
今回は確認しなかったが、過去については途中からずっと、自分の発表の以外は録音も禁止と言われ続けている事も、念のために一々ここに書いておく。
後で、そんな事は全然ありませんでした、と揉み消される恐れがあるからだ。
そう成る恐れがあるぐらいに十分に不審な規則だ。
2011年秋季大会の報告記事で対話文の詳細な公開を行なった事がキッカケである事は明白だ、と思っている。
前回あたりから、素粒子論の発表会場で毎回同席するS氏の私への妨害工作が、判然として来た。
前回は、私が登壇して自分のノートPCに会場のケーブルを接続しようとしていると、聴講席最前列に座ったS氏が、過失を装って、私が使うケーブルを、自分の方へ引っ込めてしまった。
今回は、私の順番が回って来た時に、S氏が降壇を故意に遅らせたので、私は、座長に、もう登壇しても良いですか、と尋ねる必要が生じた。
私が登壇した際に、まだ壇上に残っていたS氏は、私の失敗回避を悔しがる「ちくしょー」という発語をした。
セッション終了後、自分の荷物の片付けをしていると、2014年春季大会の報告記事で指摘されているクリック音をS氏が数回鳴らすのが聞こえた。
これは、S氏が犯人連に加入した事の明白な印、であった。
2014年春季大会の会場での発表妨害クリック音の発音者もS氏であった可能性もあるが、S氏がクリック音を鳴らすのを聞いたのは、2015年秋季大会の今回が初めてだろう、と思う。
S氏は、クリック音を私に聞かせた後直ぐに、何事も無かったかの様に私に挨拶(接近を伴わない)をして退室したが、犯人が犯行直後に被害者の眼と鼻の先を何食わぬ顔で悠然と通過する、という行動パターンが典型として存在する。
被害者に、暴力を振るわせたり言葉で咎めさせたりして、被害者を陥れるのが目的だ、と考えられる。
S氏を犯人連が勧誘しているのを見掛けたのは、2009年春の立教大学の会場ではなかったか、と思う。
その時には、S氏は誘いに乗りそうにない感じに見えたが、その後、勧誘に応じたのだろう。
犯人連は、「なあ、あんなやつ、もう放っておいて、我々の仲間に入れよ」と言うのだろう。
そういう態度を私は非難しないが、放っておかず集めた仲間で不正な手段を使って立ち向かって来るのは、非難の対象である。
判然とでなければ、S氏の存在は、毎回同席する様に成った当の最初から怪しかった。
学会での私の発表の様子を伝聞する人に、実際とは違った様子を想像をさせる目的と、S氏が質問する事によって質疑応答時間を圧迫する目的が、思い当っていた。
2014年秋季大会の報告記事の末尾に書かれている、ノートPCと会場設備を接続するケーブルに関する罠においても、単にS氏が誤ってケーブルを脚で引っ掛ける事が犯人によって期待されていただけではなく、S氏も故意に脚をケーブルに引っ掛ける予定だった疑いが濃厚だ、と2014年秋季大会の会場で私が思ったのが、S氏の工作が限度を超える事が判然とし始めた時だった。
発表前に私に雑談をさせて、発表直前の準備を妨害し、発表内容を劣化させる、という工作をS氏が過去に何度もして来た事も間違いない、と思う。
これについては、私から話し掛けた事も多いし、私が雑談には応じないという意思表示をハッキリ行えば、断れる状況だった。
ある時期を境にS氏のその傾向がピタッと消失し、誰かに言われたらしい、と感じた。
ハードウェア的犯行に切り替わったのは、その時期が境ではないか、と思う。
帰路、香川県のホテルレオマの森に立ち寄って1泊した。
そこから自宅に帰る際に、岡田駅までホテルのシャトルバスで移動した。
岡田駅に到着して切符を購入する為に列に並んでいると、タマネギの臭いがすると同時に、シャトルバスの運転手が私の方を向いて顔をしかめた。
過去に他所で何度も経験した事が有る定番の嫌な臭いだった。
2015年09月27日正午の少し前の事だった。
私がシャトルバスの運転手に、タマネギの臭いがしますね、と言うと、シャトルバスの運転手は、しますねえ、という意味の返事をした。
これは、シャトルバスの運転手が私の事を快く思わず私の顔を見ながら顔をしかめた、という風に私が誤解した、という事実をデッチ上げる為の工作だったろう、と思っている。
私がワザワザ、タマネギの臭いがしますね、と言ったのは、その事に気を回して、誤解の芽を未然に摘み取る為だった。
従って一般論として、自分に対して顔をしかめた人に怒っている人が居て、顔をしかめた原因を怒っている人が誤認していても、その事は怒っている人の何らかの欠陥の証拠とは見なせない。
因みに、タマネギの臭いは、私の自宅の中で何者かによって過去に多数回用いられて来た。
本当にタマネギによる物なのかは不明だが、そんな感じの臭いであり、嫌な臭いだ。
し尿のアンモニア臭との類似性が非常に強いから、ではなかろうか。
さらに、私がまだ学生だった頃から、ポテトサラダ等の食品に生タマネギが入れられる様に成り、今に至るまで、私はこれに大きな不都合を感じて来た。
近年では、カレー店やハンバーガー店で経験した。
いずれも、私を狙った嫌がらせだと確信している。
宿泊中も、バイキング形式の夕食と朝食の際には、前回までと同様に、主に多数の客が連携した通行トラブル仕掛けが熾烈だった。
程度の差こそあれ、これは、前日に宿泊した天王寺のホテルでの朝食の際にも同様であり、近年は、どこに行ってもしつこく付きまとわれている。
何年か前に名古屋のホテルに宿泊した際には、盆が除去されていたらしく、皿を盆の様に使って大いに不便した。
このケースでは、ホテルも犯人に協力している事が分かる。
客室に顕著な不審異音が聞こえる事は、近年は何処に宿泊しても必ず付いて回っていたが、今回は非常に少なかった。
椅子に細工がしてあるらしかった事が過去には有ったが、今回は十二分に立派な異なるデザインの椅子だった。

2013年09月26日の記事@即達