
since 2003
イレコナビ サイトマップ
日本物理学会2015年春季大会での私の発表は、文法物理学についての22aDG-6「宇田方程式の多体量子力学描像」および物理教育についての24pCK-10「ソレダケノモンの数理(2)」の2つだった。
発表旅行中に撮影された写真は、私の写メール投稿ブログ「即達」の2015年03月分のページに掲載されています。
DG会場は、早稲田大学早稲田キャンパス14号館4階403教室だった。
仙台高等専門学校の松枝宏明さんによる22aDG-1「エンタングルメント・エントロピーからの重力場方程式の導出」の質疑応答時間に、次の様に質問した。
| 宇田 | 先行する質問の言い換えみたいな物に成りますが、どんな計量でも、とまでは言えないかもしれませんが、色々な計量に対して、それを解に持つアインシュタイン方程式が存在するわけで、これは、その計量を解に持つ様にエネルギー運動量テンソルを決める事が出来る、という事に過ぎません。 発表者は「重力場方程式を導出した」と言いますが、それは、情報幾何から出て来るフィッシャー計量をアインシュタイン方程式が解に持つ様にアインシュタイン方程式中のエネルギー運動量テンソルを決めた、という事ですか? |
| 松枝 | はい、そうです。 それに加えて、そのエネルギー運動量テンソルに情報幾何的な意味付けを行なった、という事です。 「重力場方程式を導出した」というのは、言い方が良くなかったかもしれません。 |
会議の主催者に録音を禁止する権利が法的には有るのか否か、後でキチンと調べたい。
22aDG-1の発表開始前に、この講演の講演概要を読んで私は、これは大変な物かもしれない、と独り言を言ったが、それは買いかぶりだった。
常葉大浜松総研の中村正義さんによる22aDG-3「曲面上の量子力学-G(x) = 0 vs. (d/dt)G(x) = 0 -」の質疑応答時間には、次の様に質問した。
| 宇田 | 同じ系に対して普通用いられているラグランジアンとは異なる別のラグランジアンを用いても同じ結果が得られる、という内容ですか? |
| 中村 | 使ったラグランジアンは、普通用いられている物と同じです。 ・・・の項を含むラグランジアン、 |
| 宇田 | その部分が普通のラグランジアンと違うのではないですか? |
| 中村 | はい、違います。 |
| 宇田 |
ラグランジアン以外に付加的な条件を使いましたか? 古典運動方程式も同じに成りましたか? |
| 中村 | 付加的な条件は使っていません。 古典運動方程式については確認していません。 |
拘束条件の演算子を状態ベクトルに作用させるとゼロベクトルに成る、という付加条件を使うのではなかったか、と思ったので、付加条件を使っていない、という返答にも納得しなかった。
使った、という返答を得た上で、使った付加条件が普通の付加条件とどう違うのか、質問しようと思ったのに。
この発表は、講演概要に私の学生時代の卒業研究の先生の論文が引用されていて、その意味で気に成った。
多分、東京農工大学工学部の松崎清司さんによる22aDG-4「SO(4) Standard model and Quanta with Flavour」の質疑応答時間に、次の様に質問した。
| 座長 | その仮説の必要性は何ですか? |
| 発表者 | 既存の理論では zitterbewegung(Bjorken & Drell, Relastivistic Quantum Mechanics, p.38)が生じてしまうが、私の仮説では、それが解消される。 |
| 宇田 | zitterbewegungというのは粒子が光速でジグザグに運動する物だったと思いますが、それはそれで良いのではないか。 zitterbewegungは無くさなくても良いのではないですか。 |
| 発表者 | zitterbewegungが有ると、ジグザグ運動で向きを変える時に何か他の存在から力を受けている事に成ってしまう。 |
| 宇田 | そうとは限らない、と思います。 |
「それはそれで良い」という私の意見は、相対論的量子力学でzitterbewegungが生じるが、場の量子論ではzitterbewegungは生じないので、zitterbewegungが生じる事は、相対論的量子力学が相対論的量子力学として変更されるべきである事を意味するものではなく、文法として正しいのは相対論的量子力学ではなく場の量子論だ、という事を意味する、という意見です。
22aDG-6「宇田方程式の多体量子力学描像」では、液晶プロジェクターで資料を掲示しながら、次の様に口述した。
| 発言タイミング | 発言内容 | 注釈 |
| OHP-sr-1 | 今回は、前回の発表で私が持ち出した力学系の量子力学を考えます。 これは、宇田方程式の離散化描像です。 |
左記発言開始は、2015年03月22日午前11時49分19秒頃です。 |
| OHP-sr-2 | (OHP-sr-2の冒頭の方程式を指して)これが宇田方程式です。 Φより左の部分をハミルトニアンと見ると、エネルギー・ゼロの定常状態を決める方程式の形をしています。 tは時刻ですが、Φより左の部分をハミルトニアンと見なす時には、時刻tは自由度の番号の役割を担います。 時間をε刻みで離散化し、運動量演算子について前回発表した特定を行なうと、ハミルトニアンは、(OHP-sr-2中のH0の定義式を指して)この様なH0と、それから(OHP-sr-2中のH1の定義式を指して)この様なH1の和の形に書けます。 H0は、自由粒子のハミルトニアンの和と見なせます。 H1は、粒子間の相互作用を表し、隣り合う粒子間の相互作用の和に成っています。 隣り合う粒子間の相互作用が、ノイマンが測定を表す為に導入した物と同じ形をしている事は、私の理論の有望性の現れだ、と感じます。 次の時刻での位置が前の時刻での位置を測定する事によって量子状態の時間発展が生じる、というのが私の理論の正しい解釈なのかもしれません。 まず、自由粒子1個のハミルトニアンの固有ベクトルを求めます。 固有値eに属する固有ベクトルを決める方程式は、座標表示では、(OHP-sr-2中の左辺に赤のアンダーラインが引いてある式を指して)こう成ります。 この方程式の解は、(OHP-sr-2中の{の右の漸化式を指して)これらの漸化式に従う係数列を用いて、(OHP-sr-2中の{の左に書かれている式を指して)こういうべき級数で表されます。 漸化式を解くと、係数列の一般項は、(OHP-sr-2の最後の2つの式を指して)こう成ります。 ただし、ガンマ関数の変数が複素数でも(OHP-sr-2の右下隅の楕円内に書かれている式を指して)この公式が成り立つ物と仮定しました。 そう仮定しなくても、式が汚く成るだけです。 この様に、係数列の偶数項と奇数項は完全に独立なので、各固有空間は2次元だと分かります。 |
- |
| OHP-sr-3 | 各固有空間の基底ベクトルは、座標表示では、べき級数の(OHP-sr-3の左上隅の式を指して)奇数項だけ取ったこの関数と、偶数項だけ取った(OHP-sr-3の最上段の右の式を指し忘れて)この関数の2つです。 これらの関数に座標演算子と運動量演算子を作用させると、各項の冪指数が1だけズレて、関数の偶奇が入れ替わる事は明らかなので、演算子の作用の詳細は、この様な(OHP-sr-3の2行目のξ1を指して)ξ1, (OHP-sr-3の2行目のξ2を指して)ξ2, (OHP-sr-3の3行目のη1を指して)η1, (OHP-sr-3の3行目のη2を指して)η2で表現し尽くされる、と分かります。 前のスライドの係数列の一般項を使ってξ1,ξ2,η1,η2を具体的に求めると、結果はこう成りました。 (OHP-sr-3の4行目の式を指して)これと、(OHP-sr-3の5行目の式を指して)これと、(OHP-sr-3の6行目の式を指して)これと、(OHP-sr-3の最後の式を指して)これ。 (OHP-sr-3の最後の式の右辺のデルタ関数の変数を指して)ここでデルタ関数の変数が複素数に成っていますが、この点が不安です。 どの式も成ってますけど、ここ複素数に成ってますね。 |
- |
| OHP-sr-4 | この点について考えてみました。 デルタ関数のフーリエ積分表示を拡大使用して、変数が複素数の場合のデルタ関数を、(OHP-sr-4の左上隅の式を指して)この式で定義してみます。 前のスライドの式を導き出す時に、(OHP-sr-4の1行目の右の式を指して)この式を使ったので、この式の証明を試みます。 そのために、複素平面内での、(OHP-sr-4の赤色の長方形を指して)この様な閉曲線に沿った、(OHP-sr-4のグラフの下の1行目の式を指して)この線積分を考えます。 曲線で囲まれた領域内に被積分関数の特異点は無いので、積分結果はゼロに成るはずです。 曲線の4つの辺に対応する部分を分けて書くと、この様に成ります。(OHP-sr-4のグラフの下の2行目の等号を指した) (OHP-sr-4のグラフの下の2行目の辺を指して)右に進む部分、(OHP-sr-4のグラフの下の3行目の辺を指して)上に進む部分、(OHP-sr-4のグラフの下の4行目の辺を指して)左に進む部分、(OHP-sr-4のグラフの下の5行目の辺を指して)下に進む部分です。 上に進む部分は(OHP-sr-4の]の左の1行目の式を指して)この様に書き直され、下に進む部分は(OHP-sr-4の]の左の2行目の式を指して)この様に書き直されるので、xの絶対値を無限大にする極限で(OHP-sr-4の右下の長方形枠内上段を指した)f(x+iy)の絶対値が限りなくゼロに近づくなど、aの絶対値を無限大にする極限で(OHP-sr-4の]の左の1行目の式中のf(a+iy)を指して)f(a+iy)と(OHP-sr-4の]の左の2行目の式中のf(-a+iy)を指して)f(-a+iy)の差がゼロに限りなく近づく場合には、(OHP-sr-4の右下の長方形枠の下段を指して)a=2nπを保ちつつaの絶対値を無限大にする極限を取ると、上に進む部分と下に進む部分の対は、キャンセルします。(OHP-sr-4の]の右の0を指した) したがって、最初の2項の和もゼロでなければいけません。 つまり、(OHP-sr-4の∴の右の等号を指して)こうです。 (OHP-sr-4の∴の行の右辺を指して)この積分は、実変数のデルタ関数しか含まないので、(OHP-sr-4の最終行の辺を指して)こう成る事が元から分かっています。 これで、証明が出来た事に成ります。 ただし、aの値を2nπに限定した事と、(OHP-sr-4の右下の長方形枠全体を指した)fに対して変数の実部が大きい場合の条件を課した事が、証明の暗い部分です。 |
- |
| OHP-sr-5 | 話を元に戻します。 (OHP-sr-3の1行目の2つの式を指して)これらの関数の直積、これを(OHP-sr-5の左上隅の式の末尾の因子を指した)座標表示に持つベクトルを、全空間の基底ベクトルとして用いると、一般のベクトルはこの様に書けます。(OHP-sr-5の左上隅の式の等号を指した) 因みに、今考えている問題においては、このベクトルは量子状態ではなく量子歴史を表すベクトルです。 このハミルトニアンの(OHP-sr-2のHを指した)固有値ゼロに属する固有ベクトルを決める問題は、(OHP-sr-5の長方形で囲まれたHΦ[x]=0を指して)HΦ=0に成る様な(OHP-sr-5の左上隅の式中のAを指して)Aを求める問題に帰着します。 この問題の解を摂動法で1次の項まで求めました。 そのために、βを摂動パラメータとして、(OHP-sr-5の左上隅のセルの右隣の2行を指して)この様に置きました。 元の問題はβ=1の場合であり、べき級数は収束しそうにないので、元の問題とは異なる問題を解く事に成り、結果は定性的な意味しか持ちません。 --- 基底ベクトルへのH0の作用(OHP-sr-5の1個目の長方形枠の上の式の左辺を指した)は、(OHP-sr-2のuの定義式を指して)基底ベクトルの定義から、こう成る事が(OHP-sr-5の1個目の長方形枠の上の式の中央辺を指した)分かり、D0をこう(OHP-sr-5の1個目の長方形枠を指した)定義すれば、基底ベクトルへのH0の作用は、この様に(OHP-sr-5の1個目の長方形枠の上の式の右辺を指した)略記できます。 --- 基底ベクトルへのH1の作用は(OHP-sr-5の2個目の長方形枠の上の式の左辺を指した)、H1の(OHP-sr-2のH1の定義式を指した)定義と、(OHP-sr-3の2行目と3行目を指しながら)XとPの作用の表現を使うと、この様に書けます。(OHP-sr-5の2個目の長方形枠の上の式の中央辺を指した) ここで、D1をこの様に定義すると(OHP-sr-5の2個目の長方形枠を指した)、基底ベクトルへのH1の作用は、この様に略記できます。(OHP-sr-5の2個目の長方形枠の上の式の右辺を指した) --- これらの表現を使うと、HΦ=0という条件は(OHP-sr-5の最後の長方形枠を指した)、この様に書けます。(OHP-sr-5の最後から2番目の式を指した) この式と基底ベクトルの線形独立性から、基底ベクトルの係数は全てゼロでなくてはいけない事が分かります。 したがって、こうです。(OHP-sr-5の最後の式を指した) この式に、(OHP-sr-5の右上隅の方のA[e,i]の式を指して)これを代入し、 |
- |
| OHP-sr-6 | (OHP-sr-6の冒頭の式を指して)両辺のβ0の係数を等しいと置くと、こう成ります。 両辺のβ1の係数を等しいと置くと、こう成ります。(OHP-sr-6の2行目の式を指した) --- この式と(OHP-sr-6の冒頭の式を指した)、D0の定義より、この式(OHP-sr-6の3行目の式を指した)が得られ、この条件を満たすA0の中からエンタングルしていない歴史に対応する物を一つ選んで書いたものが、これです。(OHP-sr-6の最後から2番目の式を指した) この式(OHP-sr-6の2行目の式を指した)とD0とD1の定義より、この式が得られ(OHP-sr-6の4行目のスペースを指した)、これにこのA0を(OHP-sr-6の最後から2番目の式を指した)代入すると、A1はこうだと分かります。(OHP-sr-6の最後の式を指した) ここの分母は全ての(OHP-sr-6の最後の式の右辺の分数を指した)eの和ですが、ek-1までと(OHP-sr-6の最後の式の・・・δ(ek-1)を指した)それから(OHP-sr-6の最後の式のδ(ek+2)・・・を指して)ek+2以降はデルタ関数でゼロに出来ます。 このA1は、このA1の全体はですね(OHP-sr-6の最後の式の左辺を指した)、H1によってエンタングルが生じる事を示しています。 ここの分数係数(OHP-sr-6の最後の式の右辺の分数を指した)がekの関数とek+1の関数の積に成っていない事を見るだけでも、エンタングルが生じている事は分かります。 隣り合う粒子だけがエンタングルしている状態の和が全状態だ、というのが結論です。 |
左記発言の終了は、2015年03月22日午前11時58分44秒頃です。 |
画像をクリックすると拡大画像が表示されます。
| 講演概要 |  22aDG-6 |
日本物理学会講演概要集・第70巻・第1号(ISSN2189-079X)・21ページより。 | ||||
| OHP |  OHP-sr-1 |
 OHP-sr-2 |
 OHP-sr-3 |
 OHP-sr-4 |
 OHP-sr-5 |
 OHP-sr-6 |
2015年03月22日撮影分@学会発表の実況@動画
この発表の原型はwww.GrammaticalPhysics.ac > Forum > Problems > Theory of Quantum History Entangled in Time-like Direction Discretized Quantum Mechanical Modelです。
質疑応答時間には、次の様な対話が生じました。
| 発言者 | 発言内容 | 注釈 |
| 鈴木貞吉氏 | 最後の所の、そのA0とA1ありますよね? |
- |
| 宇田 | はい、あります。 | - |
| 鈴木 | A2は、どうなんですか? | - |
| 宇田 | A2以降は求めていません。 | - |
| 鈴木 | Akがどういう風に成るか、という事を言わないと、なんか中途半端な様な気がするんですけどねえ。 | - |
| 宇田 | そうですねえ、全く中途半端だと思います。 あの、逆にですねえ、これは、先ほど申しました様に、β=1の問題であるのにβが小さい場合でしか通用しない摂動法という物を用いているので、高次の項を求めてもしょうがない、というのは有るんですよ。 だから、初項だけ求めて、定性的に何が起こるか、というのを大雑把に見てみる、様子を見てみる、という、そういう事ですねえ。 まあ、言い逃れに近いですけれど。 ま、それも、ちょっと悪く言い過ぎなんですけどねえ、うん。 まあ、そういう論法なんですが。 |
1次の摂動項までしか求めない、というのは、教科書等でも良く有る事です。 |
| 座長 | すみません、普通の量子力学と違う所は、どういう所が違うんでしょうか? | - |
| 宇田 | はい、普通の量子力学と違うとこはですねえ、これは一番最初に2005年に発表した物なんですが、新文法という事でですねえ、このtは時間なんですが、普通の量子力学ではtは時刻ですが、その普通の量子力学で時刻として現れて来るtが、私のこの方程式においては自由度の番号の様に成ってる、つまり、χ(t)というのが、t番目の自由度の座標である、といった扱いに成ってるんです、うん。 という意味で違う、はい。 |
- |
2015年03月22日午前10時05分から午前10時07分までの間の何時かに、DG会場内に「ホー」という機械音が持続的に聞こえ始めた。
22aDGでは、私の発表終了直後に鈴木さんの発表資料が表示されず、鈴木さんの22aDG-7の発表開始が遅れた。
私の後始末の不備や私による故意の嫌がらせを疑わせる為の工作が有ったらしい、と思った。
これまでは、学会会場では、私に対する攻撃だけだったが、私が攻撃したという事実を捏造しようとする仕掛けが始まった、と思った。
最初は鈴木さんのパソコンの不調が疑われ私もそう思っていたが、会場設備のスイッチが切られていたのが原因だと分かり、それを知って工作の可能性が高いと思った。
高田馬場駅から早稲田大学早稲田キャンパスまで移動するために高田馬場駅でバスに乗って運賃を運賃箱に入れようとモタついていると、運賃をまだ入れていないのに、発車するので後方に移動して下さい、と運転手から言われ、慌てて運賃を運賃箱に入れて数歩後方に移動するとバスは直ぐに発車した、という事があった。
運賃の支払い中は発車を待ってくれるだろう、と見込んで乗っての事だったが、東京は違ったかな、と思い、次回以降は乗る前に財布から運賃を出す様にしたら、その間発車を待った運転手も居たので、初回のはやはり仕掛けだった様だ。
自宅を出発する前に、バス運賃用の小銭は、A9ポリ袋に片道1回分を入れて、それを財布の硬貨室に入れておいたので、モタツキは度を過ぎた物ではなかった。
バス運賃用の小銭の準備をこの様に入念に行なう様に成ったのは、過去の経験からだが、その過去の経験も怪しいらしい、という事が、今回の事で分かった。
また、初回往路バス車内では、私にスマホを覗き見させて反則を取ろうと狙う者も居た。
DG会場で見たあの人だったかもしれない。
CK会場は、早稲田大学早稲田キャンパス11号館7階704教室だった。
24pCK-10「ソレダケノモンの数理(2)」では、液晶プロジェクターで資料を掲示しながら、次の様に口述した。
| 発言タイミング | 発言内容 | 注釈 | |||||||||||||||||||||||||||||||||||||||
| OHP-13-1 | 宇田雄一です。 今回は、どの先生がどの生徒を教えるかを決める原理について発表します。 日本物理学会2014年春の大会での発表の続編です。 |
左記発言開始は、2015年03月24日16時04分56秒頃です。 | |||||||||||||||||||||||||||||||||||||||
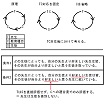
| OHP-13-2 | 先生をT、教育種目をC、(OHP-13-2の上段の3行2列の表を指した)生徒をSで表すと、これら3者の相互選択の原理は、ソレダケノモン的には、この様に(OHP-13-2の上段左の図を指した)、TがCを、CがSを、SがTを選択する、という物です。 | - | |||||||||||||||||||||||||||||||||||||||
| 選択結果の全体を一度に求めるのは難し過ぎるので、TC対応毎に分けて考える事にします。(OHP-13-2の上段中央の図を指した) TC対応を固定すると、CS対応はTS対応だと見なせます。(OHP-13-2の上段右の図を指した) |
|||||||||||||||||||||||||||||||||||||||||
| 全てのTC対応についてTS対応を求めた後で、その中から最善のTS対応を生むTC対応を探せば、選択結果の全体が分かります。 | |||||||||||||||||||||||||||||||||||||||||
| 無償の自由教育の場合について、TS対応を決める条件として、これら2つの条件(OHP-13-2の下段の2行2列の表を指した)を作ってみました。 ただし、先生にとって生徒が好ましい、とは、その先生の教育種目へのその生徒の適合度が高い、という事です。 それ以外の意味での好ましさは全て差別に当たる物として排除されるべきです。 |
|||||||||||||||||||||||||||||||||||||||||
| これらの条件は、現実社会で少なくとも建前としては是とされている事を、四角四面に書いただけです。 両性の合意のみに基づく結婚も、これです。 自由契約は全てこれです。 |
|||||||||||||||||||||||||||||||||||||||||
| OHP-13-3 | 先生も生徒もN人だとし、それらを1からNまで(OHP-13-3の最上段の変数設定を指した)の自然数で表す事にします。 | - | |||||||||||||||||||||||||||||||||||||||
| Tの志望状況をこの様な表で表す事にします。(OHP-13-3の2段目左の表を指した) T=1の第1志望はS11(OHP-13-3の2段目左の表中のS11を指した), T=1の第2志望はS12(OHP-13-3の2段目左の表中のS12を指した), 第3志望はS13(OHP-13-3の2段目左の表中のS13を指した)。 T=2の第1志望(OHP-13-3の2段目左の表中のS21を指した)、第2志望(OHP-13-3の2段目左の表中のS22を指した)、第3志望(OHP-13-3の2段目左の表中のS23を指した)。 T=3の第1志望(OHP-13-3の2段目左の表中のS31を指した)、第2志望(OHP-13-3の2段目左の表中のS32を指した)、第3志望(OHP-13-3の2段目左の表中のS33を指した)など、という風に成っています。 |
|||||||||||||||||||||||||||||||||||||||||
| Sの志望状況をこの様な表で(OHP-13-3の2段目右の表を指した)表す事にします。 S=1の第1志望はT11(OHP-13-3の2段目右の表中のT11を指した), 第2志望はT12(OHP-13-3の2段目右の表中のT12を指した), 第3志望はT13(OHP-13-3の2段目右の表中のT13を指した)。 S=2の第1志望(OHP-13-3の2段目右の表中のT21を指した)、第2志望(OHP-13-3の2段目右の表中のT22を指した)、第3志望(OHP-13-3の2段目右の表中のT23を指した)。 S=3の第1志望(OHP-13-3の2段目右の表中のT31を指した)、第2志望(OHP-13-3の2段目右の表中のT32を指した)、第3志望(OHP-13-3の2段目右の表中のT33を指した)など、という風に成っています。 |
|||||||||||||||||||||||||||||||||||||||||
| TS対応を関数Zで表す事にします。(OHP-13-3の3段目の式S=Z(T)を指した) | |||||||||||||||||||||||||||||||||||||||||
| (Tの志望状況表のS11,S21,S31,・・・を指しながら)S11,S21,S31,・・・が全て異なる場合は、Si1=Z(i)(OHP-13-3の最下欄の文中の式Z(i)=Si1を指した)は条件1の解です。 任意のiに対して、Si1がT=iよりも高く評価する先生は、仮に居るとしても、既に第一志望の生徒を取っており、その先生にとって第一志望の生徒は必ずSi1よりも好ましい、からです。 |
|||||||||||||||||||||||||||||||||||||||||
| また、この場合、Si1=Z(i)は条件2も満たします。 任意のiに対して、T=iがSi1よりも高く評価する生徒は居ないので、仮に居たらどうだ、という命題は常に真だからです。 |
|||||||||||||||||||||||||||||||||||||||||
| 同様にして、(Sの志望状況表のT11,T21,T31,・・・を指しながら)T11,T21,T31,・・・が全て異なる場合は、i=Z(Ti1)(OHP-13-3の最下欄の文中の式Z(Ti1)=iを指した)は条件1と条件2の両方の解です。 | |||||||||||||||||||||||||||||||||||||||||
| (OHP-13-3の最下欄の文の冒頭のS11,S21,S31,・・・を指しながら)S11,S21,S31,・・・が全て異なり、(OHP-13-3の最下欄の文の冒頭のT11,T21,T31,・・・を指しながら)T11,T21,T31,・・・も全て異なる場合、前者は先生の意志であり後者は生徒の意志であるから、両者は独立であり、従って、この解と(OHP-13-3の最下欄の文中の式Z(i)=Si1を指した)この解は(OHP-13-3の最下欄の文中の式Z(Ti1)=iを指した)、一般には異なります。 従って、条件1の解も条件2の解も一般には一意でない、と分かります。 また、競争関係は、先生間と生徒間で別々に存在するのではなく、先生が第一志望の生徒を取ると生徒が第一志望の先生に就けない、生徒が第一志望の先生に就くと先生が第一志望の生徒を取れない、という風に、先生の希望と生徒の希望も一般には対立する物である事が分かります。 |
|||||||||||||||||||||||||||||||||||||||||
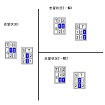
| OHP-13-4 | N=2の場合について(OHP-13-4の志望状況1の欄を指した)、その様子を具体的に見てみましょう。 志望状況1では、Z(1)=1, Z(2)=2は条件1,2の解であり、 先生の希望と生徒の希望が同時に叶えられています。 志望状況2では(OHP-13-4の志望状況2解1の欄を指した)、Z(1)=1, Z(2)=2は条件1,2の解だが、 これでは、先生の希望のみが叶えられ、生徒は妥協しています。 志望状況2では(OHP-13-4の志望状況2解2の欄を指した)、Z(1)=2, Z(2)=1も条件1,2の解だが、 これでは、生徒の希望のみが叶えられ、先生は妥協しています。 この様に、志望状況に応じて、先生と生徒の間に競争関係が存在したりしなかったりしています。 志望状況2では、解が一意でない事が分かります。 |
- | |||||||||||||||||||||||||||||||||||||||
| OHP-13-5 | N=3の場合を見ると、志望状況によっては、先生と生徒の間の綱引きの様な不定性が存在する事が分かります。 先生が第一志望の生徒を取り、生徒が第三志望の先生で妥協する解。(OHP-13-5の左の上段を指した) 先生も生徒も第二志望で妥協する解。(OHP-13-5の左の中段を指した) 先生が第三志望の生徒で妥協し、生徒が第一志望の先生に就く解。(OHP-13-5の左の下段を指した) この様に、同一の志望状況に対して3つの解が存在します。 ここまで解明してみて、このうちの1つの解のみを提示し、条件1や条件2に訴えて、こうするしか仕方ありませんよね、と言って先生や生徒をだましている人が居るのではないか、と思う様に成りました。 先生が生徒に第1解のみを提示して生徒をだましたり、生徒が先生に第3解のみを提示して先生をだましたり、という可能性です。 |
- | |||||||||||||||||||||||||||||||||||||||
| OHP-13-6 | この様に、3人の先生の志望内容が全く同じで、3人の生徒の志望内容も全く同じ場合、解は、人気の有る人は人気の有る人同士、人気の無い人は人気の無い人同士で師弟関係を結ぶ、という内容に成り、もっともらしい。 この場合、解は1つだけで、不定性は有りません。 |
- | |||||||||||||||||||||||||||||||||||||||
| ここまでの具体例を見て、解には、先生と生徒の綱引きの形での不定性が残るだけで、開放かスクミかの形での不定性は生じそうにない、と予想されます。 つまり、先生と生徒が足並みを揃えて希望が叶うか妥協するかの不定性は生じそうにない。 また、不定性は志望がバラける事によって生じるらしい事も分かります。 |
|||||||||||||||||||||||||||||||||||||||||
| OHP-13-7 | 最後に、条件1と条件2が同値である事を、証明します。 先生による志望序列表がこうだとし(OHP-13-7の最上段左の表を指した)、生徒による志望序列表をこうだとすると(OHP-13-7の最上段右の表を指した)、 (OHP-13-7の3行2列の表中の条件1の式の該当箇所を指しながら)条件1は、T=iの生徒の序列表でのT=iの順位よりもkが小さいならば、T=iの生徒の第k志望の先生の序列表でのその先生の生徒の順位は、その先生の序列表でのT=iの生徒の順位よりも小さい、つまり上位だ、という風に書けます。 (OHP-13-7の3行2列の表中の条件2の式の該当箇所を指しながら)条件2は、T=rの序列表でのT=rの生徒の順位よりもsが小さいならば、T=rの第s志望の生徒の序列表でのその生徒の先生の順位は、その生徒の序列表でのT=rの順位よりも小さい、つまり上位だ、という風に書けます。 条件1の対偶は、これ(条件1の式の⇒より右の部分を指した)の否定ならばこれ(条件1の式の⇒より左の部分を指した)の否定、という命題だから、こう成ります。(OHP-13-7の3行2列の表中の第3行を指した) この表式において、この変数変換を行なうと(OHP-13-7の最終行の変数変換の式を指した)、 (条件1の対偶の式の⇒の左の不等式の左辺を指して)この不等号の左の部分がsに(条件2の式の⇒の左の不等式の左辺を指した)、(条件1の対偶の式の⇒の左の不等式の右辺を指して)不等号の右の部分が(条件2の式の⇒の左の不等式の右辺を指した)この不等号の右の部分に、 そして、(条件1の対偶の式の⇒の右の不等式の左辺を指して)こっちの不等号の左の部分が(条件2の式の⇒の右の不等式の左辺を指して)これに、そして(条件1の対偶の式の⇒の右の不等式の右辺を指して)不等号の右の部分が(条件2の式の⇒の右の不等式の右辺を指して)この不等号の右の部分に一致するので、 条件1の対偶と条件2が同じに成ります。 したがって、条件1と条件2は同値です。 さて変数変換の内容ですが、これはiの値毎に分けて考えると、分かります。 ここでiを固定すれば(変数変換の左の式中のiを指した)、これは順列関数なので(変数変換の左の式中のλを指した)、ここはλが順列関数なので、この条件でkとrが一対一に対応し(変数変換の左の式中の等号を指したらしい)、この条件でsは(変数変換の右の式中のsを指した)T=rの序列表での(変数変換の右の式中のπrを指した)Z(i)の順位という事だから、sはrの関数に成ります(変数変換の右の式中のsを指した)、この条件で。 したがって、rもsもk,iの関数として指定できています。 (変数変換の左の式中のλZ(i)を指した)これは順列関数だから、kを変えるだけでrは全範囲動きます。 iを動かしても合わせてkを変える事によってrを一定に出来、(変数変換の右の式中のZを指した)Zも(変数変換の右の式中のπrを指した)これも順列関数だから、そうやってiを変えれば(変数変換の右の式中のsを指した)sは全範囲を動きます。 従って、(k,i)から(r,s)への写像は上へのです。 逆に、右の式はiをr,sの関数として与え(変数変換の右の式を指した)、それを左の式に代入すると(変数変換の左の式を指した)、kがr,sの関数として決まります。 以上によって、(k,i)と(r,s)は全範囲一対一対応が付いています。 |
左記発言終了は、2015年03月24日16時15分11秒頃です。 |
|||||||||||||||||||||||||||||||||||||||
画像をクリックすると拡大画像が表示されます。
| 講演概要 |  24pCK-10 |
日本物理学会講演概要集・第70巻・第1号(ISSN2189-079X)・3524ページより。 | |||||
| OHP |  OHP-13-1 |
 OHP-13-2 |
 OHP-13-3 |
 OHP-13-4 |
 OHP-13-5 |
 OHP-13-6 |
 OHP-13-7 |
2015年03月24日撮影分@学会発表の実況@動画
質疑応答時間には、次の様な対話が生じました。
| 発言者 | 発言内容 | 注釈 |
| 座長 | さっき等号が無かったんですが、良んですかねえ? | - |
| 宇田 | それは等号の無い場合についてしか調べてません。 等号が入ると難しい問題に成るので、今回は、その問題については、まだ調べてません。 |
- |
| 座長 | 対偶という風に言うんだったら、等号が気に成ったんですが。 | A < B の否定は A≧B であって A > B ではない、という観点からの指摘です。 |
| 宇田 | 最初の問題設定が、講演概要に書いてあるんですが、ここでですねえ、たとえばT=1について第1志望、第2志望、第3志望とか並べてますが、途中でイクオールは無い、という前提で問題解いてます、はい。 そういう問題しか解いてません。 あ、述べてませんねえ、ええ、述べてません。 そういうのを使ってます。 鋭い御指摘だと思います。 |
先生にとって異なる生徒の好ましさが等しい事は無い、あるいは、等しい場合でも必ず便宜上どちらかを上位に置きどちらかを下位に置く、という前提の下で考えたので、その事を宇田は何とか言おうとしています。 「述べてません」というのは、発表中にこの前提条件を宇田が述べなかった、という意味です。 「鋭い」という形容詞を宇田は肯定的な意味で用いました。 |
| 座長 | これは何かに解決するスキームを与えますか? | - |
| 宇田 | 解決するスキーム? | - |
| 座長 | はい、この手法が何かを解決することは有るでしょうか? 有るとすれな何か? |
- |
| 宇田 | やっぱり、個人個人の権利を明らかにして、どの範囲がその人の権利であるか、というのを理論的に究明して行こう、という物で、色々な人の権利侵害を防ぐ、まず第一歩として研究してる、というのは有ります。 | ソレダケノモン方式教育全体が何を解決するか、を宇田は言おうとしています。 今回の発表内容は、ソレダケノモン方式教育の部品です。 スキームと言われて、ソレダケノモン方式教育をスキームだと思った。 今回の発表だけについて言えば、マッチングにおける納得の達成、という問題に解決するスキームを与える事が期待できるでしょう。 |
| 座長 | 具体的適用事例というのは何か考えていますか? | - |
| 宇田 | 適用事例は無いです。 無いですが、例えば、まあ、具体例で言ったら、こういうのは有りますよねえ。 一つ暴いたのは、どこだったかなあ、例えばですねえ、これですか、このうちの「1つの解のみを提示し条件1や条件2に訴えて、こうするしか仕方ありませんよね、と言って先生や生徒をだましている人が居るのではないか、と思う様に成りました。先生が生徒に第1解のみを提示して生徒をだましたり、生徒が先生に第3解のみを提示して先生をだましたり、という可能性です」と。 こういう事を明らかにする事によって、そういう事が出来なく成りますよね、私がこういう事を暴けば。 |
- |
| 座長 | 実はそこの部分、実は引っ掛かっちゃって私。 騙すとか騙さないとか、なんかそういう事ではない側面の方が強くって、意に反してそういう風に言われてしまうと、それはちょっと嫌じゃないですかねえ。 そういう場面って、どういう時に有るんでしょうねえ? 実際そういう事は、 |
- |
| 宇田 | これをもし私が初めて明らかにしているとすれば、そういう事が有ったとしても、故意ではないですから、偶然そう成っているだけだから、騙しているわけではないですが、まだ誰も気付いてないとしても、そういう事が出来るというのは気に入らないじゃないか、という意見です。 理論的にこうであれば、誰もまだしてないかもしれないけど、故意にそういう事が出来てしまう。 だけど、私がこの様に暴いてしまえば、もう、そういう事は故意に出来なく成ってしまう。 そういう事ですねえ。、 |
- |
| 座長 | マッチングの話ですよねえ、これ。 | - |
| 宇田 | マッチング、はい、そうです。 | - |
| 座長 | 要するに。 | - |
| 宇田 | はい、そうです。 | - |
| 座長 | ちょっと、まだ理解できてない部分が有るんですけども。 | - |
| 宇田 | 10分ではね、ちょっと、なかなか、難しいですね。 | - |
| 座長 | 何を明確にしようとしてるんですか、じゃあ? もう一回確認すると。 |
- |
| 宇田 | ええとですねえ、だから、明確にしようとしてるのは、この条件1と条件2というのは、これは、具体的に言うとどういう物なのか、という所ですかね。 | - |
| 座長 | その条件は妥当なのかな? | - |
| 宇田 | あ、それは大いに議論の余地が有ると思います。 私は、もう、これは非常に妥当な物だ、と思ってますが。 それは、疑問を持たれて、 |
今回の私の発表内容は、条件1と条件2の妥当性を検討する為の判断材料としても、役立ちます。 |
| 座長 | それは違うかもしれませんねえ。 | - |
| 宇田 | かもしれないですね。 | 何にでも可能性だけなら常にある、という認識に立脚しての発言です。 直前の発言を、心理的ゆさぶりや演出効果を狙った物だ、と感じたので、熱冷まし的にコレを言う必要を感じた。 |
| 座長 | 教育という場面においては、それは利害の為に取ってない、と思うんですねえ。 | - |
| 宇田 | そうですか? | 宇田の発表内容は、普通の意味では、先生が利害の為に生徒を取る事を前提とする物ではありませんが、たとえその方が生徒の為に成るからという理由であっても、教えたい事を教えたい生徒に教える、という目標が良く達成されている場合はそうでない場合に比べて先生に利益をもたらしている、という考え方が瞬間的に脳裏をよぎったので、「そうですね」とは言わず、聞き流す意味の相槌を打った。 一見すると言う必要の無い事を言ってる、うっとうしい発言に見えるかもしれないが、何も言わないと後で事実と違う解釈を付けられる危険性が有るので、こういう局面でも、しつこく一言入れる様に心掛けた。 それじゃあまるで私が「先生は生徒を利害の為に取る」と言ってるみたいじゃないか、という反発を感じて、とっさに傍聴者の誤解を未然に防ぐ一言を入れようとした。 そういう一言としては「そうですね」が有効だから、「そうですね」と言おうとしたが、上に書いたような理由で「そうですか」に変更した、という事が、一瞬の内に頭の中で起こったのだった、と思う。 因みに、つまづいてから転ぶまでの間に論理演算を6つほど行なった、と感じた事が私には有る。 これに似ている。 しかし、そういうとっさの機転に大事が掛かっていては危なっかしくていけない、と私は前々から思っている。 |
| 座長 | 公平性の観点で多分なさってると思うし、利害でそういう事でやってないんじゃないかなあ。 | 公平性については、私の今回の発表もそれを目指した物だ、と思っています。 |
| 宇田 | あん、じゃあ、この条件を認める認めない、については、ちょっと意見が食い違うかもしれません。 即座には私も、なかなか、そこについてまでは、述べる事が出来ませんが。 |
- |
| 座長 | それは、ちょっと違う気がするんだけど、 |
- |
| 宇田 | ああ、そうですか。 |
- |
| 座長 | なんか、条件設定が、なんか。 | - |
| 宇田 | ええ、じゃあ、また | - |
| 座長 | 現実的ではない気がしますねえ。 | - |
| 宇田 | はい、じゃ、また、それについて発表でもして下されば、見る事も出来ます。 | - |
| 座長 | それ、違うと思う。 あのう、相性って有りますからね、先生と生徒、学生の。 |
- |
| 宇田 | そうですねえ。 | - |
| 座長 | そういう面では一意じゃないんじゃないですかねえ、これは。 | - |
| 宇田 | それは、だから、あの、適合度というのに入れたらどうでしょうか。 あの、教育 |
この時は、瞬間的に、相性は適合度に含まれるかな、と思ったが、後で違うと思う様に成った。 相性というのは組んだ後でないと分からない事であり、相手を自由に選択する事はそれに逆行する場合もある、というのは、離婚事例に見られる通りだ。 かと言って選択の自由を否定する理由には成らないだろう。 実際問題としては事前には知り得ないような事まで事細かにあげつらうならば、原理的にはやはり相性も適合度に含まれるのかもしれない。 |
| 座長 | ええと、まあ、時間なんで、ちょっと、あの、後、あの、よろしくお願いします。 | - |
| 宇田 | はい。 | - |
| 座長 | はい、どうも有難うございました。 | - |
| 宇田 | 有難うございました。 | - |
24pCKセッション開始直前には、私の動画撮影を阻止しようとする工作が前回までより執拗だった。