
since 2003
イレコナビ サイトマップ
日本物理学会2014年秋季大会での私の発表は、物理教育についての9aAC-7「ソレダケノモンの数理(1)」および文法物理学についての20pSE-2「新文法版量子論の離散化古典描像」の2つだった。
発表旅行中に撮影された写真は、私の写メール投稿ブログ「即達」の2014年09月の記事に掲載されています。
AC会場は、中部大学春日井キャンパス9号館2階925教室だった。
AC会場では自分の発表の前に、9aAC-2「慣性力の力の教え方についての考察2」で、静止した質点を回転系で観測する場合を例示すればよい、という私が日本物理学会2008年春季大会25pRC-12で発表したのと同じ意見の人が居たのを見た。
9aAC-3「A Demonstration of the Electrical Oscillation by use of R-L-C Circuits」の発表は英語での発表だった。
質疑応答時間には私の右隣に座っていた人が英語で活発に発言していた。
質問者が発表者をボコボコにしている感じがした。
質問者に過言な所が有れば発表者を弁護してあげたかったが、発表も質問も良く聴き取れなかった。
聴き取れなかったので、質問者が「抵抗器には抵抗が有ります。電流は流れます。抵抗器とコイルを繋げれば繋がります」という風に自明な事をまくし立てる様に言っていた可能性すら、私には否定できない。
しかし、質問→返答→質問→返答なし、という流れだったので、たぶん発表者が質問者にやり込められていたのだろう。
自宅に帰って講演概要を読んでみたが、どこが新しいのか、よく分からなかった。
私の発表は9aAC-7「ソレダケノモンの数理(1)」だった。
発表前に、液晶プロジェクターで掲示する為の画像ファイルを自宅に置き忘れている事に気付き、会場で数十分間かけて即席で代替画像ファイルを作成した。
下の画像欄では、両方見る事が出来ます。
9aAC-7「ソレダケノモンの数理(1)」では、液晶プロジェクターで資料を掲示しながら、次の様に口述した。
| 発言タイミング | 発言内容 | 注釈 |
| - | 宇田英才教室の宇田雄一です。 ソレダケノモンの数理について発表します。 私の手違いで、自宅で準備したスライドが表示できないので、先ほど即席で作った物を、表示いたします。 今回は、生徒の性質関数と能力関数が与えられた時、どういう選択が予想されるか、それぞれの選択が何を意味するか、を発表します。 日本物理学会2014年春の大会での発表の続編です。 |
発言開始は午前11時06分31秒でした。 |
| OHP-13-1 | 最初に、前回発表した性質関数と能力関数について、おさらいも含めて、追加の説明をします。 まず、性質関数です。 生徒の積極度をx とし、学習結果をz とし、性質関数をz=f(x)とします。 その積極度で学習してb以上の結果が得られるならaまでなら積極度を上げたい、という事が、グラフ上の任意の点(a,b)について言える。 これが性質関数の定義です。 性質関数は、学習種目ごとに、また生徒ごとに異なります。 --- グラフが全体として左に寄っているのが「怠け者」で、全体として右に寄っているのが「働き者」。 全体として上に寄っているのが「虫が良い」、全体として下に寄っているのが「人が良い」事に対応します。 両者は独立ではなく、つまり、怠け者か働き者か、という事と、虫が良いか人が良いか、という事は独立ではなく、怠け者は虫が良い、働き者は人が良い、という相関がある事がグラフから分かります。 --- b2>b1なるグラフ上の2点(a1,b1)と(a2,b2)を考える時、b2以上の結果が得られるならば、b1以上の結果が得られるからa1までなら積極度を上げたいはずです。 一方、b2以上の結果が得られるならばa2までなら積極度を上げたいわけだから、a2までなら積極度を上げたい事はa1までなら積極度を上げたい事の十分条件でなくてはいけません。 したがってa2>a1です。 つまり、fは単調増加関数でなければいけない、と分かります。 |
OHP-13-1中では、(a1, b1)を誤って(a1, a2)と書いています。 |
| 次に、性質関数の特徴を表す指標を、幾つか導入します。 必要最低結果は、それより低い結果が保証されただけでは全くやる気が出ない結果値です。 これは、腰の重さを表します。 「重い腰を上げる」という慣用表現の意味での腰の重さです。 ドラマに出て来る「そんなハシタガネで俺が動くとでも思っているのか」という台詞は、必要最低結果の大きさを表しています。 妥協率は、必要最低結果から保証結果を少しだけ吊り上げた時の、それに対する積極度の増加率です。 妥協率は「ゲンキンさ」を表します。 限界積極度は、保証結果を幾ら吊り上げても、これ以上は積極度を上げたくない、という積極度の上限です。 漸近線のx座標が限界積極度です。 限界積極度は、怠け者か働き者かや、執念の有無によって変わります。 --- たとえば、死ぬまで頑張る、という積極度を考えれば、限界積極度は有って当然だ、という事が分かります。 積極度の絶対的な上限は限界積極度だけであり、それ未満の上限は、もっと大きな積極度に対する結果の応答が不明だ、という理由によってしか顕在化しません。 もっとやればもっと出来る、という事が分かれば、中間的な上限は上に移動します。 その種目に全く興味が無い生徒や何でも出来るだけ怠けたい生徒の性質関数は、必要最低結果が無限大、あるいは限界積極度がゼロ、という特別な場合として理解されます。 結果はそれ自体で満足が決まり、努力が無駄に成ったなんてケチな事は考えない、という意見については、そういう人のfは必要最低結果が0, 妥協率が∞, 限界積極度が∞って事であり、性質関数の概念への論駁とは見なされない、と考えます。 また、人生を棒に振る、という慣用表現の存在が、そんな人は居ない事を物語っています。 |
死ぬまで頑張る、という選択は、しないのが普通です。 これは、死ぬまで頑張るという積極度より下に限界積極度が存在している、という事を意味します。 人生を棒に振る、という慣用表現は、投入した資源が無駄に成った事に力点を置く物です。 人生を棒に振っても構わない人なんて居ないから、努力が無駄に成った事を気にしない人なんて居ない、と推測できます。 |
|
| OHP-13-2 | 次は能力関数ですが、能力関数ですね。 能力関数をz=g(x)とする時、積極度xで学習した場合、g(x)を超える結果を得るのは無理だが、g(x)以下のどの結果も有り得る。 これが能力関数の定義です。 能力関数も、学習種目ごとに、また生徒ごとに異なります。 --- x=0でもg(x)=0ではなく、x=0から出発してxを増加させて行くと、最初は指数関数的な増加が見られ、その後上限から来る頭打ち傾向が出て来る、という形に書いておきました。 グラフが上に寄っているほど才能が有り、下に寄っているほど才能が無い。 左に寄っているほど要領が良く、右に寄っているほど要領が悪い、と言えます。 両者は独立ではなく、才能が有る人は要領が良く、才能が無い人は要領が悪い、という相関が有る事がグラフから分かります。 |
- |
| 能力関数の特徴を表す指標を、幾つか導入します。 限界結果は、いくら積極度を上げても、それ以上の結果は得られない、という、結果の上限です。 これは、非常に嫌われ易い意見だと思いますが、たとえば、どんなに脚力を鍛えても月までジャンプする事は不可能だ、という言い方をすれば、誰も反論しないと思います。 月まではジャンプ不可能というのは上界の存在ですが、上界が有れば上限が有る、という数学の理屈を使うと、上限が有る事も分かります。 種目を限定しなければ、人間には無限の可能性が有る感じはします。 限界結果の高さが表す才能を奥行才能と名付けてみました。 奥行才能は、枯渇し難さであり、アウトプットモードで出しても出しても次が出て来て枯渇しない才能です。 「おい、まだあるんか?」と驚かれる類の才能が奥行才能です。 十分積極度は、その積極度で最大結果が出るので、それ以上積極度を上げる必要が無い、その様な積極度です。 正確には、g(x)が限界結果の九十何パーセントに達するxの値、という風に定義すると良いでしょう。 十分積極度は、同じ事をするのに他人より苦労しなければいけないのか他人より楽にこなせるのかの目安に成ります。 十分積極度が高ければ苦労し、低ければ楽です。 獲得済能力は、トレーニング開始時の能力であり、今後トレーニングしなかった場合の結果、つまり積極度ゼロの場合の結果で表す事が出来ます。 非常に小さいxに対してはg(x)は(1個目の式を指して)この様な指数関数で表されると仮定し、この式中のアルファベットの小文字のkを呑み込み才能と名付けてみました。 呑み込み才能は呑み込みの早さ、つまり、初歩の段階での吸収の速さを表します。 --- 呑み込み才能は受動的な学習才能で、奥行才能は能動的な研究才能です。 呑み込み才能の優劣を知った事で奥行才能の優劣を知ったと早合点する事の危険性を指摘しておきたい、と思います。 過去のトレーニングの事まで考えると、獲得済み能力は、時間軸の原点の選択の問題に過ぎないので、本質的ではありません。 現在までの学習量を積極度に換算した場合、それをbだけ増やす事は、x軸の原点を右にbだけずらす事に相当します。 すると、グラフの式は、(1個目の式を指して)この1行目の式から(2個目の式を指して)2行目のこういう式に変化し、獲得済み能力はexp(kb)倍に成ります。 ここで用いたa,bは性質関数の説明で用いたa,bとは関係ありません。 |
- | |
| OHP-13-3 | ここまでが前回に対する補足した詳しい説明なんですが、ここからが今日の本論みたいなもんですが。 性質関数と能力関数を重ねて表示すると、x-z平面は3種類の領域に分割されます。 一つは、性質的に満足だが能力的に不可能な領域です。 (領域①を指して)この丸1番の所ですね。 そして、もうひとつは、能力的に可能で性質的にも満足な領域。 (領域②を指して)これが丸2番ですね、ここですね。 そして、三つ目は、能力的に可能だが性質的に不満な領域です。 (領域③を指して)これが丸3番です。 能力的に不可能で性質的に不満な領域もありますが、これは議論に関係しません。 --- この図から、実際にどういう積極度を生徒が選択するか推測出来ます。 それは、賭博のごとき物です。 積極度xを選択した場合の、性質的に満足な結果が出る確率の目安としてg(x)-f(x)が使えます。 (領域②中の両矢印を指して)グラフ中のこれですねえ。 この両矢印の長さに対応する様な物ですねえ、g(x)-f(x)はねえ。 g(x)が大きい場合には、低い結果が出る確率は小さいので、([g(x)-f(x)]/g(x)を指して)こちらの方が正確だ、とも言えません。 生徒による積極度の選択では、これが、②の上端のx 座標を積極度として選ぶ事にブレーキを掛けます。 また、②の左半分のx 座標を積極度として選んだ場合と同じ確率でもっと良い結果が得られるxが右半分に有るので、左半分のxは選択されない、と分かります。 確率を最大にするx を積極度として選択する事には、③に落ち難いというメリットが有るが、もっと頑張れば良かったと後悔するリスクも有ります。 ギャンブルで勝ったら、もっと賭けとけばよかった、負けたら、やめときゃよかった、と後悔するのと同じです。 --- 確率を最大にする積極度で安全に平凡な結果を出す事で妥協した人が、妥協せずに積極度を上げて高い結果を出す事に運よく成功した人に対して、自分は嫌な事を我慢しているのでお前は俺に感謝しろ、と主張するのは不当です。 逆に、妥協せずに②の上端を狙って失敗した人が、②の中ほどで妥協した人に対して、お前は卑怯者だ、と非難するのも不当です。 なぜなら、自由な選択の結果の責任は選択した人自身に帰せられるからです。 自分の胸に手を当てて聞いてみれば、違った選択をする自由だって有ったのにしなかった理由は自己的(※)な物であったはずです。 だから他人には利他的な選択をしろと要求する事は出来ないのです。 自分がどうすれば他人に何か強制できる、というものでもありませんが。 --- fとgの如何によっては②が無い、という事が起こり得ます。 fがもっと上に寄ってたり、gが下に寄ってたり、例えばそういう事ですが。 fが上に寄り過ぎていたりgが下に寄り過ぎていたりすると②が無く成ります。 fが普通より上に寄りgが普通より下に寄っているとか、gは普通より上に寄っているが、それにも増してfが上に寄り過ぎているとか、fは普通より下に寄っているが、それにも増してgが下に寄り過ぎている、という場合にも②は無く成ります。 いずれなのかによって、fが悪いのかgが悪いのか、を言う事が出来ます。 ②が無いという事は、その種目には向いていない、という事であり、どの種目も②が無ければ選択の如何にかかわらず満足な結果は得られない、という事です。 生来固有の性質と能力がそうである人は、障害者に準じる資質の持ち主として、相応の配慮を受けるべきだ、という提案を、ここでしたいと思います。 --- 因みに、グラフを見ると、②がある為には、gの傾きがfの傾きを途中で超える事が大切らしい、と分かります。 以上です。 何か質問などありましたら、どうぞ。 |
実際には、gがハッキリとは分からない、という問題も有るだろう。 ②が無い、という事は、犯罪の動機に成り得る。 ※利己的を誤って自己的と読んでいます。 積極度を上げれば満足できる確率が下がるから積極度を上げない、という選択や、積極度を上げれば成功した場合の満足度が高いから積極度を上げる、という選択における選択理由は利己的だ、と言っているのであって、それ以外の考え方をする人は居ない、と言っているのではありません。 それ以外の考え方をする人が極めて少ないのも事実でしょうけれど。 左記発言終了は、午前11時17分45秒でした。 |
画像をクリックすると拡大画像が表示されます。
| 講演概要 |  9aAC-7 |
日本物理学会講演概要集・第69巻・第2号・第2分冊240ページより。 | ||||
| 発表されたOHP |  OHP-13-1 |
 OHP-13-2 |
 OHP-13-3 |
- | - | - |
| 発表されなかったOHP |  |
 |
 |
 |
 |
 |
2014年09月09日撮影分@学会発表の実況@動画
質疑応答時間には、次の様な対話が生じました。
| 発言者 | 発言内容 | 注釈 |
| 質問者 | 前回のスライドの | - |
| 宇田 | 1個前ですね、はーい。 | - |
| 質問者 | 質問なんですけども、怠け者などの定義というのは、 | - |
| 宇田 | 何の定義ですか? | - |
| 質問者 | 怠け者体質だとか、積極的だ才能がある、っていう話だったんですけども、それは、どの様にして検査や測定というのを定義をして、その様に決定をしてるんですかねえ? | - |
| 宇田 | それは、全然してないです。 国語辞典の辞書的な意味でそう対応するだろう、といった様な事です。 |
- |
| 質問者 | その対応するけ、 数値的な、 生徒を実際に、この様な生徒を居るから、というので、 この様な生徒は怠け者体質だ、というのは、測定をしていなくて理論的に話をして行った、という感じですか? |
クリック音が何度も鳴らされている。 |
| 宇田 | まあ、そうですねえ。 どちらかと言えばそうですが、そういうほどの物でもなくて、当て字を当てて行ったというか。 どういう局面が有るかなあ?似たのと言うと、うーん。 |
- |
| 質問者 | 実際にそういうグラフが出るのに対して、何か生徒をダーッと百人なら百人対象にした物をやったのか、やっていないのか、という話なんですけども。 | - |
| 宇田 | あ、してないです。 | - |
| 質問者 | あ、してないんですか? | - |
| 宇田 | 全然してないです。 だから、怠け者という言葉の定義が別にあって、それに基づく統計データがあって、で私の方の特徴付けの基準があって、照らし合わせて、私の方の基準でここに該当する人は怠け者の定義においてここに該当する人に一致してますね、という話ではないんです。 そうじゃないんです。 そうじゃなくて、むしろね、怠け者とかいう様な言葉に定義を与えようという様な、科学的な定義を与えようといった様な物にかなり近いですねえ。 ちょっと出しますとね、ほんとはそういう言葉は無くても良いんですが、キャッチフレーズ的に一つ一つ言葉を当てておいた方が頭にも残るでしょう? |
- |
| 質問者 | ああ、はい。 | - |
| 宇田 | そんな事でね、当ててあって、例えばですねえ、怠け者というのはグラフがこれ、性質関数が左に寄ってれば怠け者、というのは、同じ結果を提示しても、それでは、その結果を得るために、私は努力したいです、という人と、私はそんな結果では努力する気が起きません、という人を分けた時に、努力したいです、という人がこれが働き者気質で、やる気が起きません、という人が怠け者気質だという | - |
| 質問者 | それは、最終的な結果というものを、人によって、興味がある、興味がない、っていうのがあると思うんで、 | - |
| 宇田 | ああ、それは、そうですね。 | - |
| 質問者 | 全体的には平均取ってしまえば、一緒に成る様な気がするんですけれども、 | - |
| 宇田 | それは、特定の種目において興味を示さないからと言って、怠け者だとは言えませんね、うん。 その部分は不正確だと思います、私の表現は、ええ。 それで、全部を総合すると、それはあるかもしれないです。 怠け者だとか働き者だとかいう様な言い方というのは、全ての種目にわたって総合すると、どの人も同じだ、というのは私は多分違うと思いますよ。 最後に「②が無い」という話が出て来ましたけど、そうするとまあ、そういう言葉(怠け者や働き者)も適切かと思いますねえ。 全部総合した結果は |
全種目に渡る平均はどの人も同じだ、という事は多分無いだろう、という意見を述べています。 |
| 質問者 | うん、総合した結果なんですけども、初めにバラつきがあって、それをまとめたら一緒に成るよね、というのをチョッと思ったので。 | - |
| 宇田 | 一緒に成るというのは? | - |
| 質問者 | 最終的に、さっき言ったみたいに、平均取ってしまえば、そういうバラつきが無く成るんじゃないかな、っていうのは、個人によっては、そういうバラつきがあるんですけども、っていうのは、そう感じただけなので。 | 質問者は、全種目に渡る平均が、どの個人についても同じに成るだろう、と言っているらしい。 |
| 宇田 | これは、まだ個人の特徴付けの話ですね。 まだね。 |
質問者が全ての個人に渡る平均の話をしている、と宇田は誤解している。 |
| 質問者 | 特徴付けですね。 ごめんなさい。 はい、ありがとうございます。 |
- |
| 宇田 | いずれは、統計的な事も、考えれれば考えたいですけども。 | - |
SE会場は、佐賀大学本庄キャンパス教養教育1号館3階133教室だった。
20pSE-2「新文法版量子論の離散化古典描像」では、液晶プロジェクターで資料を掲示しながら、次の様に口述した。
| 発言タイミング | 発言内容 | 注釈 |
| OHP-sr-1 | www.GrammaticalPhysics.acの宇田雄一です。 | 発言開始は13時48分10秒でした。 |
| 今回は、新文法版シュレディンガー方程式を旧シュレディンガー方程式に持つ連続体の古典力学を、質点系の古典力学に置き換えて明らかにし、そうする事によって、新文法版シュレディンガー方程式の内容の基本イメージを作ります。 | - | |
| OHP-sr-2 | 新文法版シュレディンガー方程式の表現のうちの、日本物理学会2011年秋の大会で発表した形が、これです。 (一番上の式を指した) これは、ポテンシャル項がゼロの場合の式です。 そろそろ宇田方程式と呼ばせて下さい。 |
- |
| 時間をε刻みで離散化すると、こう成ります。 (2段目の区画に書かれている式を指した) これは、エネルギー固有値ゼロの定常状態を決めるシュレディンガー方程式の形をしているので、ここより左の部分 (2段目の式の}を指して)この、ここより左の部分ですね。 ここより左の部分をハミルトニアンと見なす事が出来ます。 |
||
| 古典力学の形式でハミルトニアンを書き出すと、こう成ります。 (3段目の区画内の1行目の式を指した) これは、(φを指して)こういうスカラーポテンシャルと(Aを指して)こういう無限次元ベクトルポテンシャルの電磁場中を運動する(Mを指して)こういう質量と(Qを指して)こういう電荷の質点のハミルトニアンの形をしています。 ポテンシャルの方を「作用×(-1)ポテンシャル」と呼び、磁場の方を「速度磁場」と呼ぶ事にします。 最初の方程式の形から、そういう風に名前を付けるのが適当だと思います。 変数は、χからxに変更しました。 |
||
| このハミルトニアンから導かれる正準方程式は、これとこれです。 (正準方程式の段の上の式を指して)これと(正準方程式の段の下の式を指して)これですね。 物理時間tと区別して、τを論理時間と呼ぶ事にします。 (正準方程式の段の式中のτを指した) (ハミルトニアンの段の丸で囲った式を指して)この式から分かる様に、物理時間は(正準方程式の段の丸で囲った式を指して)t=jεという形でjに繋がっているのであって、正準方程式が表す時間発展の時間τとは別です。 |
||
| これら2つの式からpを消去すると、ニュートンの運動方程式として、この式が得られます。 (最下部に書かれている式を指した) |
||
| OHP-sr-3 | 考察の対象と成っている質点系は、横軸を物理時間、縦軸を位置とする座標平面内で、物理時刻がεずつ隔たった直線上に質点が1個ずつ存在し、それらが論理時間の経過とともに運動する、という物です。 古典解は、この平面内の線で表されます。 今考えているのは、宇田方程式中の物理ポテンシャル項をゼロとした自由粒子の場合だから、古典解は直線です。 |
- |
| OHP-sr-4 | ニュートンの運動方程式を図解すると、各質点に働く力は、こうです。 (左上の区画を指した) 真ん中の質点は、左右の質点からバネ定数kの弾性斥力を受けます。 また、真ん中の質点は、左の質点からは速度に比例した引きずり力を、右の質点からは同種だが逆向きの力を、受けます。 |
- |
| kとκの具体的な内容は、(右上の区画を指して)こうです。 | ||
| (左下の区画を指して)力と速度の積が運動エネルギーの増加率だから、この図から、運動エネルギーの増加率と弾性ポテンシャルエネルギーの減少率が等しい事が分かります。 なぜなら、速度に比例する力がする仕事の和はゼロだからです。 また弾性斥力に関しては、隣合う質点間で作用反作用の法則が成り立っている事が分かります。 速度に比例する力については、隣合う質点間で作用反作用の法則は成り立っていません。 |
||
| しかし、(右下の区画を指して)隣の隣の質点との関係を考えると、この様に速度に比例する力についても、作用反作用の法則が成り立っている事が分かります。 だから、考察の対象と成っている質点系はエネルギー保存則も運動量保存則も両方とも成り立つ正常な質点系だ、と分かります。 |
||
| OHP-sr-5 | (最も右上の2つの区画を指して)この様な行列A,Bを使うと、先述した運動方程式は、こう書けます。 (最も左上の式を指した) |
- |
| 第2項の係数を非常に小さい定数(初出のkを指して)kに書き換え、(x=x0+・・・を指して)xをkの冪級数に展開して、摂動法を適用してみます。 このkは前のページのkとは別です。 第2項の係数は実際には非常に小さくは出来ないので、(k<<1を含む区画の文を指して)あくまで定性的な調査と成ります。 |
||
| (k<<1を含む区画の左の区画の下の式を指して)これを(k<<1を含む区画の左の区画の上の式を指して)これに代入して、k0の係数を等しいと置いた物が(d2x0/dτ2=・・・の式を指して)これで、k1の係数を等しいと置いた物が(d2x1/dτ2=・・・の式を指して)これです。 | ||
| こっちを解くと、(d2x0/dτ2=・・・の式を指して)これを解くとx0の1階微分が得られ、それを積分してx0が分かります。 そうして得られた結果が、(dx0/dτ=・・・の式を指して)この式と(x0=・・・の式を指して)この式です。 u,v,wは積分定数であり、uとvは(v=Auを指して)この関係で結ばれる列ベクトルです。 wも列ベクトルです。 |
||
| Aが実反対称だから、exp(τA/εα)は無限次元空間内での一定の角速度での回転です。 ちょっと、ここには計算は書きませんが、この回転は(無限次元実回転の区画内の座標変換を指して)この様に古典解を古典解に移すので、古典解の空間を軸とする回転だと言えます。 |
||
| (d2x1/dτ2=・・・の式を指して)こっちを解くとx1の1階微分は、(dx1/dτ=・・・の式の1行目を指して)この様に表される事が分かり、これにx0の解を代入すると、こう成ります。 (dx1/dτ=・・・の式の2行目を指した) ここで([A,B]-=0を指して)行列Aと行列Bが交換する事を使うと、(dx1/dτ=・・・の式の3行目を指して)こう成ります。 積分結果は、(dx1/dτ=・・・の式の4行目を指して)こうです。 w'は積分定数であり、Aw'=Bwである様な列ベクトルです。 |
||
| 以上の計算結果をまとめると、1次までの摂動近似では、論理速度ベクトルは、(最下部に書かれている式を指して)こう成ります。 講演概要には、w'=0の場合を、書いておきました。 一定のハシタベクトルを除けば、ゆっくり変化するベクトルを一定の角速度で回転させた物に成っています。 2013年春の大会で発表した描像とも特徴が一致します。 |
||
| OHP-sr-6 | 初等力学の問題に、頂上での位置エネルギーに等しい力学的エネルギーを持って一様重力場中で滑らかな円周を登る質点が頂上に到達するまでに掛かる時間は無限大だ、というのが有ります。 | 円に上る時間が無限大に成る事は エネルギー保存から求めたdt/dθを積分すれば分かる。 |
| これに対して、今考えている問題では、頂上での論理位置エネルギーに等しい論理力学的エネルギーを持って、一様な速度磁場中で、作用ポテンシャル山に、巻き付きながら歴史荷電質点が、無限の論理時間を掛けて頂上イクオール古典解まで登ります。 前のページの計算でそれを証明できたわけではありませんが、前のページの計算結果と2013年春の大会での発表内容から推測すると、そう言えます。 2013年春の大会では、論理時間の経過に伴って永久に限りなく古典解に近付き続ける、という事が、物理時刻の個数を3にまで減らした簡単化された系について示されています。 |
- | |
| 古典解の実現確率が高い、という事情は、古典解の任意に小さい近傍への滞在時間が無限大だ、という状況として表現される、と解釈できます。 論理時間が有る程度以上経過すると、その後ずっと歴史質点がほとんど古典解に静止したままに成ります。 |
- | |
| OHP-sr-3 | これは、このグラフで言うと、赤色の質点が全て古典解を表す灰色の直線に寄って行く、という事です。 と思いきや、そう成るのは物理速度がゼロの古典解についてだけである事に、講演準備中に気付きました。 物理速度がゼロの古典解は、このグラフでは水平な直線で表されます。 |
- |
| OHP-sr-4 | (左下の区画を指して)この図を見れば分かる様に、物理速度がゼロの古典解の位置エネルギーはゼロですが、物理速度がゼロでない古典解の位置エネルギーは負です。 弾性力による位置エネルギーに着目すれば、そうだと分かります。 |
- |
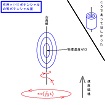
| OHP-sr-7 | この事情を反映させて、作用×(-1)ポテンシャルの等ポテンシャル面を描くと、こう成ります。 序盤に述べた様に、論理エネルギー固有値がゼロの定常状態の古典対応物を考えているのだから、論理力学的エネルギーはゼロだとせねばなりません。 したがって、物理速度がゼロの古典解に無限の論理時間を掛けて限りなく近付く事は有り得ますが、物理速度がゼロでない古典解に無限の論理時間を掛けて限りなく近付く事はかなり無さそうです。 これが宇田方程式の致命的な欠点であるかどうか即座には判断できませんが、少なくとも、古典解の近傍で滞在論理時間が無限大に成るので古典解の実現確率が高い、という解釈は成り立たない、という事が言えます。 そういう解釈が成り立つためには、等ポテンシャル面は(右上隅の図を指して)こうでなくてはいけません。 |
- |
| 物理速度が異なる古典解の位置エネルギーが異なる事は、作用汎関数がガリレイ変換に対して不変ではない、という事です。 ローレンツ不変な作用を用いれば改善されるのではないか、と思いますが、こんな所で相対論の必要性が出て来る物なのかは疑問です。 自由クラインゴルドン場の作用は、どの古典解に対してもゼロに成りそうです。 以上です。 質問どうぞ。 |
左記発言終了は、13時59分38秒頃でした。 |
画像をクリックすると拡大画像が表示されます。
| 講演概要 |  20pSE-2 |
日本物理学会講演概要集・第69巻・第2号・第1分冊13ページより。 | |||||
| OHP |  OHP-sr-1 |
 OHP-sr-2 |
 OHP-sr-3 |
 OHP-sr-4 |
 OHP-sr-5 |
 OHP-sr-6 |
 OHP-sr-7 |
2014年09月20日撮影分@学会発表の実況@動画
この発表の原型はwww.GrammaticalPhysics.ac > Vintage(2008-2014) > Forum > Grammatical Physics > Products of Grammatical Physics > Theory of Quantum History Entangled in Time-like Direction > Discretized Classical Model of the New Equationです。
質疑応答時間には、次の様な対話が生じました。
| 発言者 | 発言内容 | 注釈 |
| コメント者 | 質問というかコメントなんですけど、今の話を聞いて、一般相対性理論というのは、時空の物理で、だから論理時間とかを考えてしまうと、新しい時空みたいな、そういう拡張が必要じゃないですか。 で、一般相対論によって宇宙とか膨張してるので、だからその論理時間に対してそういう一般相対性理論を使ってみたら、もしかしたら、何かホントは膨張してるんじゃなくて、我々の論理の何て言うんでしょう、我々の時間がこうチョッと変な感じに成ってて膨張に見えてる、という、何かそういう可能性とか |
論理時刻の各々に対しては、4次元宇宙が対応します。 一方、宇宙膨張という概念は、物理時刻の各々に対して4次元宇宙の3次元断面を対応させる物です。 したがって、宇宙膨張が論理時間の経過に従って進行する、という事は有り得ません。 論理時間の経過に従って起こる宇宙膨張という物が有るならば、それは、我々の言い慣わして来た宇宙膨張ではなく、4次元空間が膨張する、という新種の膨張です。 |
| 宇田 | うーん、ちょっと、そういう風な事は無いだろう、という印象は受けますが、やってみた事は無いです。 | |
| 質問者 | 論理時間っていうのは何でしたっけ? すみません。 |
- |
| 宇田 | 論理時間? 論理時間はですねえ、私自身も分かりません。 私自身も何の事やら分からない新概念なんですが、流れで説明するしか無いんですけど、宇田方程式というのがですねえ、定常状態を決める方程式の形をしてます。 定常状態を決める方程式で、ここには物理概念しか出て来てないんですが、論理時間は出て来てません。 そうすると定常状態を決める方程式というのは、その方程式を得るために量子化する前の系を考えると、そこでは時間発展の古典力学があるわけですね。 そこに戻すと、時間発展の古典力学というものがあるから、何か時間の概念というのがあるはずなんですが、それを勝手に論理時間と名付けて。 実際にそのような現象が起こってる、というのではないんですね。 私自身、何かは分からない。 これから明らかにして行かなければいけない新しい物を見付けた、という、そういう感じです。 |
旧量子力学において定常状態を決める方程式は時間を全く含んでいない。 一方その元になった古典力学には時間の概念が含まれている。 前者から後者への移行は、時間が付け加わる、という特徴を持つ。 これに倣うと、宇田方程式を、定常状態を決める方程式とみなす時、古典力学に相当する理論への移行において、何らかの時間が付け加わるはずだが、物理時間は宇田方程式中に既に登場しているので、付け加わるのは物理時間ではない。 そこで、論理時間という新概念の存在の必要性が生じた。 参考: 曖昧な概念で明瞭な概念を定義する事@動画 |
ここまでに書き出した様な対話内容詳細を用いない限り、「宇田の発表内容は支離滅裂だった」とか「宇田が意思疎通不能者だという事が発表を見てよく分かった」とか「宇田の失礼な態度に怒らなかった相手は立派だ」というデマを流された場合に、その被害を防止・軽減する事は、ほとんど不可能である。
そして、私は過去に、そういうデマを、たくさん流された。
ただし、「宇田の失礼な態度に怒らなかった相手は立派だ」というデマは、記憶に無い。
おそらく、そういう犯罪に対して発言内容詳細を公開する事によって打ち勝ったのは、私が初めてであろう。
その事は、この犯罪が、防ぐ術を持たない者に一方的に襲いかかる、という点で、極めて卑劣な物である事を物語る。
ありがちな事がその人については違う、という場合、その人は誤解されやすい状態にある。
して見せなければ信じてもらえない程までに非常に高い能力を持った人の、その能力事実は、この一例だ。
それ程までには能力が優れてはいない、という事が、ありがちな事であり、また、自分はそのぐらい能力が優れているんだ、という風にうそぶく人ほど実際の能力は人並み以下である、という事も、ありがちな事だ。
過去に私は、あなたがもし本当に人並み外れて優れた研究結果を出したとしても、他者から理解されないだろう、という意味の事を言われた事がある。
その時は、その点についても、して見せなければ信じてもらえない程までに非常に高い能力を発揮すれば、克服できるだろう、と思った。
しかし、あなたは理解されない、と言った人の真意は、誤解を招きやすい、という弱点を最大限利用した攻撃を受けるだろう、あるいは、自分(達)がそういう攻撃をする、という意味であったようだ。
これは、「あなたは犯罪を犯す」とか「そういう奴は犯罪を犯す」という言説にも見られる事だ。
2014年09月09日午前09時31分頃AC会場に到着した。
その時に9aAC-1は既に始まっていた。
2014年09月09日午前09時38分、AC会場の窓の外から動力削岩音が、しつこく持続的に聞こえていた。
2014年09月09日午前09時49分頃、削岩音が止んだ。
その約1分後、削岩音発生が再開された。
再開は、音が止んだというメモメールを私が自分のパソコンに送信した事への反応で有り得る。
2014年09月09日午前09時58分頃から少なくとも約5分間は、削岩音が止んだままに成っていた。
その後についてはメモしていないが、ずっと止んだままではなかった。
ガガガガとかドドドドという音ではなく、電動鋸でコンクリートを切断している様なギーンという音だった。
これは、私の自宅近辺で私を陥れるために頻繁に用いられる音と、音量や音色が大体同じだった。
実際には、連絡を受けた別人が連携して発音しているのだろうけれど、どこへ行っても行った先で同じ音を聞かされると、された人は同一の犯人がつきまとっている様に感じる。
狙われた人以外はそう感じないので、狙われた人が周囲から理解されない、という構造に成っている。
異音については、前回の発表の報告記事にも、書いておきました。
また、陥れ全般については、敵の手口を暴露@空手以外@理論@武道に、書かれています。
2014年09月20日は、前の人の発表の間中自分のノート型パソコンを演壇付近の器具に接続しっぱなしにするよう、発表前に座長から勧められた。
私は、「今まで通りにしないと何かあるといけないので」と言って、それを断り、自分のパソコンを自分の席に一旦持ち帰った。
勧められた瞬間には気付かなかったが、自分のパソコンを席に持ち帰った直後、次の点に気付いた。
もし自分のパソコンを演壇付近につなぎっぱなしにしたら、前の人が発表を終えて帰る際に、足でケーブルを引っ掛けて、それで私のパソコンが床に落下し使えなくなって、私の発表がプロジェクター無しの発表に成る危険性が大きい。
そして、間違いなくその事が狙われている、と思った。