
since 2003
イレコナビ サイトマップ
経済への参加者が全員、出来るだけ負担率の小さい商品を売って稼ごうとする事により、負担率の小さい商品ほど販売競争が激しく成り、その結果、負担率の小さい商品ほどたくさん売れる確率が小さく(少ししか売れない確率が大きく)成る。
以下においては、簡単のため、負担率に個人差は無いものとし、益種格の量による差も無いものとする。
また、個人に着目する。
益種格αiの負担率をLiとし、αiが価値にしてfだけ売れる確率密度をπi(f)とする。
αiの生産量をfiとし、生産した分は全て出荷するものとする。
αiの消費量(自給自足の場合の生産量)はf0iだとする。
売り上げの期待値 = ∫0fi df f πi(f) ・・・ (1)
売り上げの期待値は消費量に一致するはずだから、
∫0fi df f πi(f) = f0i ・・・ (2)
生産負担 = Lifi ・・・ (3)
負担は自給自足の場合と同じには成らないだろう。
売れ残り分を生産する負担だけ、負担が増えるはずだ。
そこで、(負担の増加) = (売れ残り分を生産する負担の期待値) という式を書くと、
Lifi - Lif0i = Li∫0fi df (fi - f)πi(f)
∴ Li(fi - f0i) = Lifi∫0fi df πi(f) - Li∫0fi df fπi(f)
∴ Li(fi - f0i) = Lifi - Li∫0fi df fπi(f) ∵∫0fi df πi(f) = 1
∴ Lif0i = Li∫0fi df fπi(f) ・・・ (4)
オッズOiの馬券の的中確率がOiに反比例する事を参考にして、πi(f) = cLi/f としたのでは、規格化積分∫0fi df πi(f) において、f = 0 の近傍で発散が生じるので、規格化条件 ∫0fi df πi(f) = 1 が成り立たない。
従って、πi(f) = cLi/f は不可能である。
色々と試行錯誤した結果、負担率Lの益種格については x = f/fi の確率分布は次の関数πL で表される、という仮説が有望だと分かった。
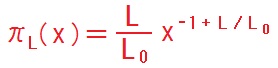
この関数は、規格化条件
∫01 dx πL(x) = 1 ・・・ (5)
を満たす。
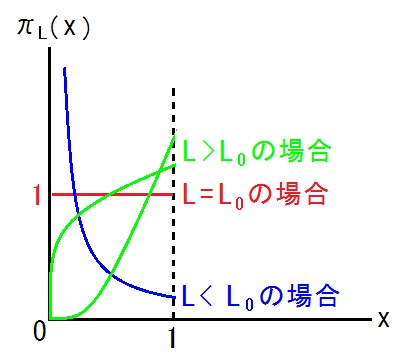
πL(x)は、低xではLの減少関数、高xではLの増加関数に成っている。
この事は、負担率が大きい益主格ほど大きな売り上げが得られる確率が大きく小さな売り上げに終わる確率が小さい、という事を意味する。
この性質はもっともらしいので、このπL(x) は本当っぽい。
πi(f)は、この関数を使って、
πi(f) df = πLi(f/fi) d(f/fi)
∴ πi(f) = πLi(f/fi)/fi ・・・ (6)
という風に表され、当然の事ながら規格化条件
∫0fi df πi(f) = 1
を満たす。
∫0fi df fπi(f) = fi∫01 dx xπLi(x) = fi(Li/L0)(1+Li/L0)
これが f0i に一致するのは、
fi(Li/L0)(1+Li/L0) = f0i
∴ fi = f0i(L0/Li)/(1+Li/L0) ・・・ (7)
こう成った場合に(4)が成り立つ事、も分かる。
つまり、仮説として(6)を採用する事は、仮説として(7)を採用する事と等価である。
∫01 dx xπ(x) = (L/L0)/(1+L/L0)
から、
xの期待値=(L/L0)/(1+L/L0) ・・・ (8)
だと分かる。
L = L0とするとxの期待値=1/2に成るから、L0は出荷量の丁度半分が売れ半分が売れ残る傾向を持った益種格の負担率だ、と言える。
そこで、L0を「半売性益種格の負担率」と呼ぶ事にする。
L0は経済定数だと考えられる。
市場統計を実測する事によって、どれが半売性益種格かを特定する事が出来る。
それが特定できれば、その益種格の生産過程を克明に分析し、その明細を作る事によって、L0の値を具体的に知る事が出来る。
まず、この段階で、複数の半売性益種格の生産過程の明細を突き合わせて比較し、明細から算出された負担率が全て同じに成らなければいけない事を使って、個々の負担の見積もりの妥当性を検証できる。
同じに成らない方が正しい、と思われれば、(6),(8)も検証の対象に成る。
間違っていれば、修正する必要が有る。
これは、理想気体の状態方程式を修正して実在気体の状態方程式を作る作業、に似ているだろう。
これによって、実地観察による負担測定のアルゴリズムを精製できる。
次に、市場統計を実測する事によって、他の色々な益種格のxの平均値を収集する。
また、それらの益種格の生産過程を克明に分析し、その明細を作る事によって、(L/L0)/(1 + L/L0) の値ごとに、Lの具体的な値を知る事が出来る。
この段階でも、xの期待値が同じである様な複数の益種格の生産過程の明細を突き合わせて比較し、明細から算出された負担率が全て同じに成らなければいけない事を使って、個々の負担の見積もりの妥当性を検証でき、それによって、実地観察による負担測定のアルゴリズムを、さらに精錬できる。
さらに、xの期待値が異なる複数の益種格の負担率の実測値の関係が(8)に従っていなければいけない事を使えば、実地観察による負担測定のアルゴリズムに、さらなるチェックを掛ける事が出来る。
こうして得られたノウハウをまとめれば、生産過程の分析による負担率の見積もりの根拠と成る理論を作る事が出来るだろう。
理論的には、売り上げの合計の期待値が自給自足での生産量の合計に等しいならば、売れ残りの期待値の分だけ負担の期待値が自給自足の負担よりも大きく成る、という条件からπを決めるべきだ。
(7)が成り立つ場合には、上掲のπは、そう成っている。
競争が、負担率の小さい益の供給者の地位の奪い合いであろうが、譲らせ合いであろうが、負担率の大きい益の供給者の地位の押し付け合いであろうが、表向きのやり方が何であろうと、自由市場原理に違反していない限りは、表に出ている事だけから底意での競争の実態を科学的に解明できる、というコンセプトを、このページで提示できたと思う。
表に出ているデータだけに基づいて隠された真実を理論的に探り当てる、という考え方は、犯罪捜査にも応用できるのではないか、と思う。
ガウスの法則を使って電場の表面積分から内部に含まれている電荷を求める、みたいなイメージだ。
また現行の制度で言うと、外形標準課税の考え方に通じる所が有りそうだ、とも感じる。
| 出 典 |
12日@2014年08月@日記 | 市場取引ギャンブル |
| 13日@2014年08月@日記 | 市場取引ギャンブル2 | |
| 14日@2014年08月@日記 | 市場取引ギャンブル3 | |
| 15日@2014年08月@日記 | 市場取引ギャンブル4 | |
| 16日@2014年08月@日記 | 負担の科学 |