
since 2003
イレコナビ サイトマップ
バックステップの跳び幅と反撃BFSの跳び幅を、大雑把に見積もりたい。
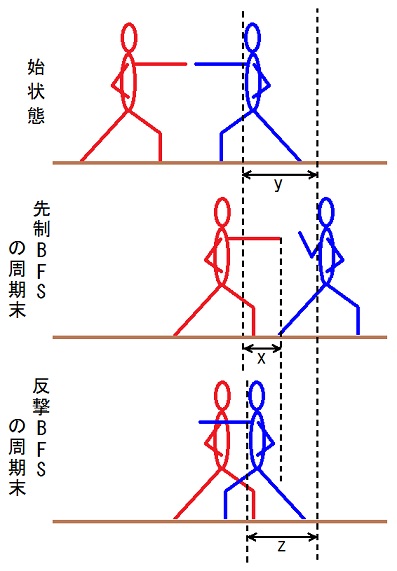
まず、始状態でのこちらの身体の前面を敵の拳先が先発BFSの周期末までに行き過ぎる距離、をxとする。
このxの定義においては仮想的に、敵は極めの後も周期末まで突き腕を伸ばしっ放しにしている、ものとする。
バックステップでの、こちらの身体の前面の後退距離をyとする。
y > x であれば、敵の拳はこちらの身体に届かない。
これは十分条件であって、必要条件は極めの瞬間の位置関係に基づく、と考えるべきだろう。
敵の拳がこちらの身体に届かない為の必要条件はそうだが、敵の先発BFSの周期末にコンタクトする様にBFSで反撃する為には、y > xである事も必要だ。
反撃BFSにおけるこちらの身体の前面の前進距離、をzとする。
こちらの拳先が敵に届くためには、z > y - x である事が必要だ。
なぜならば、z = y - x の場合に、敵の仮想拳先がこちらの身体前面にギリギリ届く位置関係に成り、したがって、こちらの拳先も敵にギリギリ届くからだ。
z > y - x という条件は厳密ではない。
なぜならば、反撃BFSの極めの瞬間には、こちらはまだ周期末の位置まで前進していないし、敵は第2撃のための動作に既に入っているかもしれないからだ。
以上をまとめると、バックステップ後先BFS成立の大雑把な条件は、
y > x and z > y - x
だと言える。
y と z の値は、与えられたxに対して、この条件を満たす範囲内で選択される。
この中で、y = z という選択を、私は良い選択だと感じる。
なぜなら、この場合には、z > y - xは自動的に満たされるし、反撃BFSの周期末における敵と自分の位置関係が、仮想的にバックステップしなかった場合の先発BFSの周期末における敵と自分の位置関係、と同じだからだ。
つまり、y = z という返し方をしたならば、当初敵がこちらに当てようとしていたBFSとほぼ同じ深さのBFSを、こちらが敵に当てる事に成る。
元々バックステップ後先BFSは、先発BFSが浅くしか入らない様に狙い付けられている場合に妥当する技なので、それ以上に浅く返すと、反撃の威力が不十分と成る恐れが有る。
こうして、大雑把な見積もりとしては、バックステップ後先BFSの跳び幅として、
z = y = x + (出来るだけチョット)
という選択に導かれる。
バックステップは前へのステップよりも困難である事を考えると、しっかりバックステップした後でチョコッと前へのステップをフォローする、といった心掛けで、大体そう成るだろう。
前へのステップは意識せず、バックステップの終点で前足を着地させず空中に保留するだけ、といった心掛けでも出来そうだ。
許容可能なxの値の範囲は、実験によって決める必要が有る。
x ≦ 0.5ウデ
ぐらいではないか、と思うのだが。
運動学的解析の結果は、もう少し厳しい(小さい上限)を示唆している。
-------------------------------------------
与えられた条件が、どういう特徴を持っている場合に、敵にとって不利、自分にとって有利であるかは、次の様にして、大雑把に見積もる事ができる。
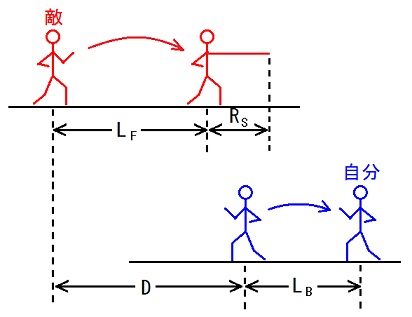
D = 重心間距離の初期値
LF = 前方へのハーフステップの跳び幅
LB = 後方へのハーフステップ(バックステップ)の跳び幅
RS = 静リーチ
まず、タイミングの事を言わなければ、前提条件として存在しているのは、先制BFSが届く事を表す条件:
LF + RS > D ・・・ (1)
および、バックステップで敵の先制BFSを交わせる事を表す条件:
LF + RS < D + LB ・・・ (2)
および、重心移動なしでは敵のパンチが届かない事を表す条件:
D > RS ・・・ (3)
および、反撃BFSが届く事を表す条件:
(D + LB - LF) - LF < RS ・・・ (4)
だけである。
(1)は、次の形に書き換えられる。
LF > D - RS ・・・ (1a)
この式が成り立つ為には、
(LFの最大値) > D - RS
つまり、
(LFの最大値) + RS > D ・・・ (1b)
である事が必要だ。
(2)は、次の形に書き換えられる。
LB > LF - (D - RS) ・・・ (2a)
(3)により、D - RS > 0 だから、
LF > LF - (D - RS) ・・・ (3a)
(2a)(3a)から、
LF > LB > LF - (D - RS) ・・・ (5)
の範囲内にLBの値を選ぶ事が可能だと分かる。
こうすれば、(4)は自動的に成り立つ。
なぜならば、(1)と(5)から(4)を導出できるからだ。
D - LF < RS ∵(1)
LB - LF < 0 ∵(5)
∴ (D - LF) + (LB - LF) < RS
LBの値をこの様に選べば、LF > LBである事によって、反撃側の時間的および体勢的優位が保証される。
この優位性のうちの特に時間的優位性に着目して、この戦術は「待ち拳」と呼ばれる事がある。←間違っているかもしれない。
LF - LBが大きいほど、反撃側が有利に成る。
LF - LB を出来るだけ大きくする事は、LBをLF - (D - RS)に出来るだけ近づける事だと、(5)から分かり、そうした場合の LF - LBが大きい事は、LF - [LF - (D - RS)]が大きい事と同値だ。
ここで、
LF - [LF - (D - RS)] = D - RS
である事を使うと、LF - LB を大きく出来る事とDが大きい事は同値だ、と分かる。
しかし、(1b)が成り立たない場合には、どうせ届かないんだから、という事で、敵は攻撃して来ないので、Dを幾らでも大きく取れる、というわけではない。
結局、敵にとって不利、自分にとって有利な与えられた条件は、Dが(LFの最大値) + RS よりも少しだけ小さい事(敵がxを小さくしか出来ない事)だ、という直感的に自明な物だ、と分かる。