
since 2003
イレコナビ サイトマップ
y = z の場合のグラフを描いてみた。
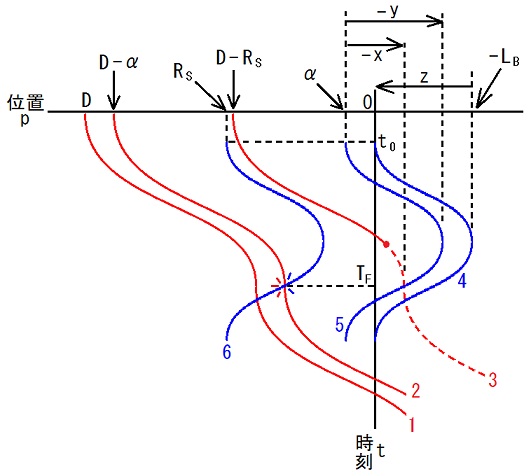
曲線1 = 敵の重心の運動(2連ハーフステップ)
曲線2 = 敵の身体前面の運動
曲線3 = 敵の仮想拳先の運動(破線部は極めよりも後)
曲線4 = こちらの重心の運動(前半がバックステップ、後半が前へのステップ)
曲線5 = こちらの身体前面の運動
曲線6 = こちらの仮想拳先の運動
t0 = 敵の開始に対する自分の開始の遅れ
TF = 前方へのハーフステップの時間周期
(曲線5の上端の位置座標) - (時刻座標がTFである曲線3上の点の位置座標) = x
(曲線5の上端の位置座標) - (曲線5の最右点の位置座標) = y
(曲線4の上端の位置座標) - (曲線4の最右点の位置座標) = z (≠定義)
曲線2と曲線6の交点が、反撃BFSのコンタクトの位置と時刻を表す。
α = 重心から身体前面までの距離(こちらと敵で共通)
D = 重心間距離の初期値
RS = 静リーチ(こちらと敵で共通)
t0の値とyの値は、次の条件を満たす範囲内で選択される。
[条件1] 先制BFSの極めの瞬間までは曲線3に曲線5が接触してはいけない。
[条件2] (曲線2と曲線6の交点の時刻座標) = TF
グラフで見ると、y > xでなくても、[条件1]は成り立ち得る事が分かる。
しかし、まあ、これは、周期末ではなく極めの瞬間を見るからなので、グラフで見なくても分かる事だ。
それでは、
(曲線5の最右点の位置座標) < (曲線3上の極め点の位置座標)
である事は必要だろうか。
必要である事がグラフから分かる。
それでは、
(曲線5の最右点の位置座標) < (曲線3上の極め点の位置座標)
でありさえすれば十分だろうか。
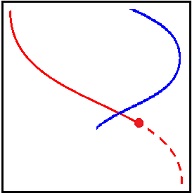
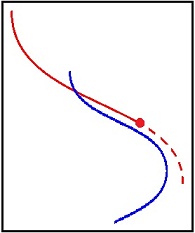
下図の様な場合があるので十分ではない、という事がグラフから分かる。
t0は、こちらの意志で値を選択できるパラメーターだが、実際問題としては、値を大きい方へ変更する自由は無い。
出来るだけ早く反応して、やっと、反撃がギリギリ間に合うぐらい、だからだ。
見て反応すれば t0 > 生理反射時間 だが、山を掛ければ t0 < 0 も可能。
山掛けが当たれば、敵の挙動は正に、飛んで火に入る夏の虫、と言えるのでは。
さて、バックステップ幅zを最小にするには、曲線5の最右点が曲線3の極め点の右に隣る様にすれば良い。
しかし、その様に調節すると、それは、曲線2と曲線6の交点の時刻がTFである事と両立しない恐れがある。
いや、一般には両立しない、と考えるべきだろう。
そこで、バックステップ幅zを最小にする事よりも、曲線2と曲線6の交点の時刻をTFにする事を、優先させる事にする。
定量的に検討してみる。
ハーフステップのページの式から、曲線6の式は、
p = RS - [h/(tanθ0)]{cosh[(t - t0)√(g/h)] - 1} ・・・ (0 ≦ t - t0 ≦ TB/2)
p = RS - LB + [h/(tanθ0)]{cosh[(TB + t0 - t)√(g/h)] - 1} ・・・ (TB/2 ≦ t - t0 ≦TB)
p = RS - LB + [h/(tanθ0)]{cosh[(t - t0 - TB)√(g/h)] - 1} ・・・ (TB ≦ t - t0 ≦ 3TB/2)
p = RS - [h/(tanθ0)]{cosh[(2TB + t0 - t)√(g/h)] - 1} ・・・ (3TB/2 ≦ t - t0 ≦2TB)
だと分かる。
ハーフステップのページの式から、
LB = [2h/(tanθ0)]{cosh[(TB/2)√(g/h)] - 1}
である事も、分かる。
曲線2の方程式は、
p = D - α - [h/(tanθ0)]{cosh[t√(g/h)] - 1} ・・・ (0 ≦ t ≦ TF/2)
p = D - α - LF + [h/(tanθ0)]{cosh[(TF - t)√(g/h)] - 1} ・・・ (TF/2 ≦ t ≦TF)
p = D - α - LF - [h/(tanθ0)]{cosh[(t - TF)√(g/h)] - 1} ・・・ (TF ≦ t ≦ 3TF/2)
p = D - α - 2LF + [h/(tanθ0)]{cosh[(2TF - t)√(g/h)] - 1} ・・・ (3TF/2 ≦ t ≦2TF)
であり、LFとTFの間には、
LF = [2h/(tanθ0)]{cosh[(TF/2)√(g/h)] - 1}
という関係式が成り立つ。
LFの値としては、LFの最大値を使う。
したがって、TFも定数である。
曲線2上のt = TF である様な点の座標は、(D - α - LF, TF)だ。
この点が曲線6の上の点でもある様にしたい。
曲線3と曲線5に着目すれば、
α - (D - RS - LF) = x
だから、
D - α - LF = RS - x
したがって、曲線6の式を使って、
RS - x = RS - LB + [h/(tanθ0)]{cosh[(TF - t0 - TB)√(g/h)] - 1} ・・・ (TB ≦ TF - t0 ≦ 3TB/2)
RS - x = RS - [h/(tanθ0)]{cosh[(2TB + t0 - TF)√(g/h)] - 1} ・・・ (3TB/2 ≦ TF - t0 ≦2TB)
すなわち、
x = [2h/(tanθ0)]{cosh[(TB/2)√(g/h)] - 1} - [h/(tanθ0)]{cosh[(TF - t0 - TB)√(g/h)] - 1} ・・・ (TB ≦ TF - t0 ≦ 3TB/2)
x = [h/(tanθ0)]{cosh[(2TB + t0 - TF)√(g/h)] - 1} ・・・ (3TB/2 ≦ TF - t0 ≦2TB)
すなわち、
TB ≦ TF - t0 ≦ 3TB/2であり、かつ、
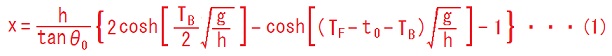
であるか、または、3TB/2 ≦ TF - t0 ≦2TBであり、かつ、
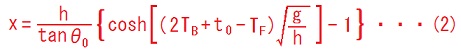
式(2)は、ハーフステップで 2TB + t0 - TF の時間だけ進む距離が x である、という風に読める。
この式は、TB, t0に課された条件、と見なされるべき物だ。
hとθ0は、こちらの意志で値を変える事が出来るが、事前に敵の目に見えるパラメータなので変化させない、と考える。
x, TFの値は与えられた条件だ、と考える。
曲線3と曲線5は、曲線2と曲線6を右にRS - αだけ平行移動して得られる曲線なので、曲線3と曲線5の交点の時刻もTFだ。
したがって、[条件1]の成立は、たぶん大丈夫だろう。