since 2003 イレコナビ　サイトマップ

< 武道 >

< 理論 >

< デザイン例 >

< バックステップ後先BFS >

< 運動学的解析(2) >

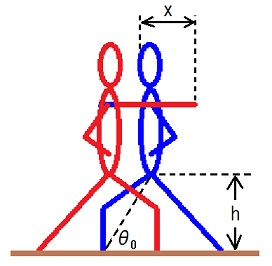
x, h, θ0, t0, TF, gに具体的な数値を代入すれば、TBが求まる。 こうして求まったTBを、TBとLBの関係式に代入すれば、LBが求まり、曲線5の詳細が確定する。 先制BFSの極めのタイミングよりもt = t0 + TBの方が早い、のか否かも見ておきたい。 xに値を代入してTBを求める、というのがコンセプトだが、式(1)(2)の形に由来する都合により、TBに値を代入してxを求める、という順序の計算を以下では行なった。 x = (h/tanθ0){2cosh[(TB/2)√(g/h)] - cosh[(TF - t0 - TB)√(g/h)] - 1} ・・・ (1) x = (h/tanθ0){cosh[(2TB + t0 - TF)√(g/h)] - 1} ・・・ (2) LB = 2(h/tanθ0){cosh[(TB/2)√(g/h)] - 1} --- g = 9.8m/s2, h = 80cm, θ0 = 60°, TF = 0.62s, t0 = 0.1s 式(1)を使った場合、 (1) x TB TF - t0 3TB/2 (t0 + TB)/TF LB 評価 7cm 0.34s 0.52s 0.51s 0.71 17cm - 9cm 0.35s 0.52s 0.53s 0.73 18cm ○ 12cm 0.36s 0.52s 0.54s 0.74 19cm ○ 14cm 0.37s 0.52s 0.56s 0.76 20cm ○ 16cm 0.38s 0.52s 0.57s 0.77 21cm ○ 18cm 0.39s 0.52s 0.59s 0.79 22cm ○ 19cm 0.40s 0.52s 0.60s 0.81 24cm ○ 21cm 0.41s 0.52s 0.62s 0.82 25cm △ 23cm 0.42s 0.52s 0.63s 0.84 26cm △ 25cm 0.43s 0.52s 0.65s 0.85 27cm △ 27cm 0.44s 0.52s 0.66s 0.87 29cm △ 29cm 0.45s 0.52s 0.68s 0.89 30cm △ 31cm 0.46s 0.52s 0.69s 0.90 32cm △ 32cm 0.47s 0.52s 0.71s 0.92 33cm △ 34cm 0.48s 0.52s 0.72s 0.94 35cm △ 36cm 0.49s 0.52s 0.74s 0.95 36cm × 38cm 0.50s 0.52s 0.75s 0.97 38cm × 39cm 0.51s 0.52s 0.77s 0.98 39cm × 41cm 0.52s 0.52s 0.78s 1.00 41cm × 43cm 0.53s 0.52s 0.80s 1.02 43cm - 式(2)を使った場合、 (2) x TB 3TB/2 TF - t0 2TB (t0 + TB)/TF LB 評価 1mm 0.25s 0.38s 0.52s 0.50s 0.56 9cm - 0mm 0.26s 0.39s 0.52s 0.52s 0.58 10cm ○ 1mm 0.27s 0.41s 0.52s 0.54s 0.60 11cm ○ 4mm 0.28s 0.42s 0.52s 0.56s 0.61 11cm ○ 1cm 0.29s 0.44s 0.52s 0.58s 0.63 12cm ○ 2cm 0.30s 0.45s 0.52s 0.60s 0.65 13cm ○ 3cm 0.31s 0.47s 0.52s 0.62s 0.66 14cm ○ 4cm 0.32s 0.48s 0.52s 0.64s 0.68 15cm ○ 6cm 0.33s 0.50s 0.52s 0.66s 0.69 16cm ○ 7cm 0.34s 0.51s 0.52s 0.68s 0.71 17cm ○ 9cm 0.35s 0.53s 0.52s 0.70s 0.73 18cm - --- h = 80cm, θ0 = 70°, TF = 0.62s, t0 = 0.1s (1) x TB TF - t0 3TB/2 (t0 + TB)/TF LB 評価 6cm 0.35s 0.52s 0.53s 0.73 11cm ○ 12cm 0.40s 0.52s 0.60s 0.81 15cm △ 18cm 0.45s 0.52s 0.68s 0.89 19cm △ 26cm 0.52s 0.52s 0.78s 1.00 26cm × (2) x TB 3TB/2 TF - t0 2TB (t0 + TB)/TF LB 評価 0cm 0.26s 0.39s 0.52s 0.52s 0.58 6cm ○ 1cm 0.30s 0.45s 0.52s 0.60s 0.65 8cm ○ 5cm 0.34s 0.51s 0.52s 0.68s 0.71 11cm ○ --- h = 80cm, θ0 = 80°, TF = 0.62s, t0 = 0.1s (1) x TB TF - t0 3TB/2 (t0 + TB)/TF LB 評価 3cm 0.35s 0.52s 0.53s 0.73 5cm △ 6cm 0.40s 0.52s 0.60s 0.81 7cm △ 9cm 0.45s 0.52s 0.68s 0.89 9cm × 13cm 0.52s 0.52s 0.78s 1.00 13cm × (2) x TB 3TB/2 TF - t0 2TB (t0 + TB)/TF LB 評価 0mm 0.26s 0.39s 0.52s 0.52s 0.58 3cm △ 6mm 0.30s 0.45s 0.52s 0.60s 0.65 4cm △ 2cm 0.34s 0.51s 0.52s 0.68s 0.71 5cm △ θ0が大きいと、動作が緩慢に成り、評価が低く成る様だ。 この様に見てみると、バックステップ後先BFSという技は、少なくとも理論的には可能な技だ、という事が分かる。 --- ※ 0.1秒は、陸上競技のスプリント走のスタートで、フライングの判断の根拠に使われている、反応の限界時間です。 ※ 私のハーフステップBFSを210フレーム/秒で高速度撮影し、29フレーム/秒で再生すると、1周期分の再生時間は約4.5秒だった。 これを元に計算すると、4.5s×29÷210 = 0.62s TFの値としては、これを使ってみた。 ※ 評価は、反撃BFSの重心運動の勢いに着目して、行ないました。 LB - x が小さければ、反撃BFSの重心運動の勢いも小さい、と考えられます。 LB - xが小さくて、評価が△や×でも、エッヂとして正拳の代わりに肘を用いれば、反撃BFSの重心運動の勢いを稼ぐ事が出来ます。 ただし、その場合には、コンタクトのタイミングは微妙に遅れます。 ※ (t0 + TB)/TFは、バックステップから反撃BFSへの切り替えが、敵の先制BFSの1周期の何パーセントが完了した時点で起こるか、を知るための指標です。 先制BFSの極めのタイミングと、反撃BFS開始のタイミングの、前後関係を知るための指標です。

最終更新2016年01月25日