
since 2003
イレコナビ サイトマップ
等競争力面
購買の意思決定のページで論じたカレーライスとオレンジジュースの競争力の比較を一般化すれば、競争力の等しい益種格を結んだ曲線(曲がっているとは限らない)を、種格平面内に描く事が出来る。
この曲線を「種格平面内の等競争力線」と呼ぶ事にする。
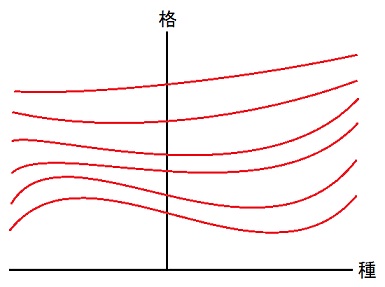
ただし、量の単位が個数である様な(体積や質量で測られて売られるのではない)益種に話を限定する。
図の様に、等競争力線は無数に有り、図に描かれている等競争力線と等競争力線の間にも、稠密に無数の等競争力線が存在している。
益種数は非常に多いが有限だ、とします。
すると、等競争力線は、
所持金初期値w円で各益種を1個ずつ購入せよ、という課題に対して平均的な人が出した答え、として定義される。
こうして定義された等競争力線は、wの値ごとに異なっているので、wを等競争力線に付けられた番号(整数とは限らない)と見なす事が出来る。
全ての益種格を1個ずつ買うのではなくて、コレとコレとコレ、という風に数個の益種を指定して、それらを1個ずつ買え、という課題の場合にも、平均的な人が出す答えは、1本の等競争力線上に収まっているだろう。
どの等競争力線上に収まっているかは、所持金初期値によって異なる。
全ての益種を1個ずつ買う、という設定は、あくまで仮想的な物であって、非現実的である。
その事は、食堂の店頭に立って、メニューを眺めている場合の事を考えれば、分かる。
全ての益種を全部食べる、なんて出来るわけない。
従って、曲線の番号wは、2点買いで等競争力線を定義した後で、競争力が等しい益種格の価格の総和を使って求められる、と解されるべき物だ。
また、等競争力線は機会によって異なる、と考えるべきだろう。
お腹をすかせて食堂の前に立っている時と、食事を済ませて食堂を出た直後では、違う事は明らかだからだ。
---
量の単位が体積や質量である場合、購買課題の前提としては、種と量を指定するやり方だけでなく、種と格を指定して量は自由に選ばせる方式や、種だけ指定して格も量も自由に選ばせる方式が、考えられる。
販売量が個数ではなく体積で測られるビールやワインについて考える場合、高級品を少量だけ買うか、廉価品を多量に買うか、という選択を迫られた経験を持つ人は多いはずだ。
この場合、異種益間の競争と違って、同種益内での高級品と廉価品の競争と成る。
益種を1つ指定した上での、所持金初期値w円で格量を1つだけ選んで買え、という課題に対して平均的な人が答えとして同程度に正しいと思う格量の集合、として「格量空間内の等競争力線」を定義する。
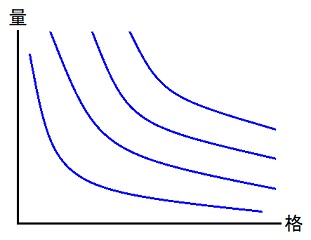
こうして定義された等競争力線は、wの値ごとに異なっているので、wを等競争力線に付けられた番号(整数とは限らない)と見なす事が出来る。
双曲線 xy = d のパラメータdに倣って、格量空間内の等競争力線の各々を格量積と呼ぶ事にする。
格量を1つだけ選んで買うのではなくて、コレとコレとコレ、という風に数個の格を指定して、それらを1個ずつ買え、という課題の場合には、今度は、平均的な人が出す答えは、1本の等競争力線上に収まっているとは限らない。
なぜなら、指定された複数の格の中の1つの格を除いて、他の全ての格の購入量をゼロとするかもしれない事が、1つの格だけ買えと言われた場合の反応から分かるからだ。
---
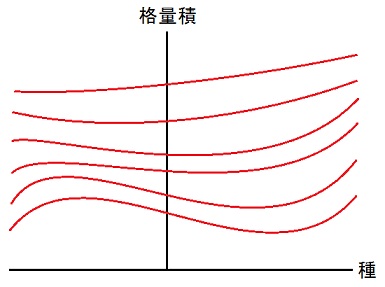
量の単位が体積や質量である場合、所持金初期値w円で、各益種の格量積を決めて、全ての益種を決めただけ購入せよ、という課題に対して平均的な人が出した答え、を等競争力面と呼ぶ事にする。
| 出 典 |
17日@2014年08月@日記 | 等競争力面 |