
since 2003
イレコナビ サイトマップ
名称=宇田雄一式ビデオ判定法。
宇田作品番号=UWV20241123.
概略の公開開始=2024年11月23日。
カメラの俯角を求める式の公開開始=2024年12月06日。
用途: 相撲でどちらの力士の身体が先に土俵の外の地面に触れたか、サッカーの試合の局面でボールがゴール・ラインよりも外に出た瞬間が有ったか否か、卓球の試合でボールが飛び去る前にテーブルの縁に触れたか否か、などを、ビデオ撮影結果に基づいて判定する。
運動科学総合研究所で高岡英夫さんが行なっている様な研究にも御活用いただける事でしょう。
早川貞一さんは、ライカの商品開発担当者にヒントとして知らせてみては、どうでしょうか。
私はオリンピックで金メダルを獲るのは無理だけど、オリンピックの審判設備は宇田工務店が一括受注みたいなもんだな、これで。
手順1: 計時中の同一のストップ・ウォッチの表示を2台のビデオ・カメラで数秒間撮影する。
手順2: 3つの長さD, H, Lを自分で決める。
手順3: Y+型配置[カメラの位置(x, y, z)=(0, D, H)]かY-型配置[カメラの位置(x, y, z)=(0, -D, H)]の位置に1台と、X+型配置[カメラの位置(x, y, z)=(D, 0, H)]かX-型配置[カメラの位置(x, y, z)=(-D, 0, H)]の位置に1台、合計2台のカメラを設置する。ストップ・ウォッチを撮影したビデオ・カメラを使う。
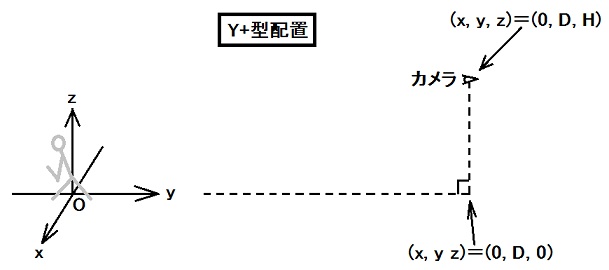
手順4: 設置した各カメラについて、第1代表点(2つのカメラに共通)、第2代表点、第3代表点を筆記具で地面(床面)に記入する。屋外の場合はゴルフのティーなどを使う。
| カメラ配置 | 第1代表点 | 第2代表点 | 第3代表点 |
| Y+型配置 | (x, y, z)=(0, 0, 0) | (x, y, z)=(L, 0, 0) | (x, y, z)=(0, L, 0) |
| X+型配置 | (x, y, z)=(0, 0, 0) | (x, y, z)=(0, -L, 0) | (x, y, z)=(L, 0, 0) |
| Y-型配置 | (x, y, z)=(0, 0, 0) | (x, y, z)=(-L, 0, 0) | (x, y, z)=(0, -L, 0) |
| X-型配置 | (x, y, z)=(0, 0, 0) | (x, y, z)=(0, L, 0) | (x, y, z)=(-L, 0, 0) |
手順5: 各カメラについて、ディスプレイのグリッド機能を援用して、第1代表点と第2代表点のn座標(撮影結果画像の上縁から下にnピクセル進んだ位置に代表点の像がある)が同じに成り、かつ第1代表点と第3代表点のm座標(撮影結果画像の左縁から右にmピクセル進んだ位置に代表点の像がある)が同じに成る様に、カメラの旋回角とロール角を調節し、ビデオ撮影を開始する。
手順6: 代表点のマーカーを除去する。筆記具での筆跡を消すとか、ゴルフのティーを除去するとか。
これを故意に残した上で「除去し忘れた」とウソをつく犯罪をしっかり防ぐ必要が有る。
マーカーをチョコレートで作っておくなども1つの方法だろう。
手順7: スポーツの試合の撮影を行なう。
手順8: 撮影結果をパソコンに取り込む。
手順9: 動画中の選手入場前の任意の1つの瞬間のフレームを静止画ファイルとして抽出する。これを2台のカメラの両方で行なう。
手順10: 各カメラについて、静止画ファイルから、3つの代表点の(m, n)座標を読み取り、その結果をm0, m1, n1, n2の値としてメモする。
| 第1代表点 | (m, n)=(m0, n1) |
| 第2代表点 | (m, n)=(m1, n1) |
| 第3代表点 | (m, n)=(m0, n2) |
手順11: 各カメラについて、D, H, L, m0, m1, n1, n2の値を基に、カメラの俯角θを算出する。
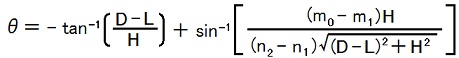
手順12: 動画中の調べたい瞬間のフレームを静止画ファイルとして抽出する。これを2台のカメラの両方で行なう。その時に、同じ瞬間のフレームを抽出するために、ストップ・ウォッチの撮影結果を参照する。
手順13: 各カメラについて、静止画ファイルを見て、ボールの中心など、調べたい点の(m, n)座標を読み取る。
手順14: 各カメラについて、θ, D, H, L, m0, m1, n1を基に、(p, q, r, u, v, w)を算出し、その結果を、第1カメラについては(p1, q1, r1, u1, v1, w1)として、第2カメラについては(p2, q2, r2, u2, v2, w2)としてメモする。
| カメラ配置 | p | q | r | u | v | w |
| Y+型配置 | 0 | D | H | -L(m - m0) | (n - n1)Lsinθ - (m0 - m1)D | -(n - n1)Lcosθ- (m0 - m1)H |
| X+型配置 | D | 0 | H | (n - n1)Lsinθ - (m0 - m1)D | L(m - m0) | -(n - n1)Lcosθ- (m0 - m1)H |
| Y-型配置 | 0 | -D | H | L(m - m0) | -(n - n1)Lsinθ + (m0 - m1)D | -(n - n1)Lcosθ- (m0 - m1)H |
| X-型配置 | -D | 0 | H | -(n - n1)Lsinθ + (m0 - m1)D | -L(m - m0) | -(n - n1)Lcosθ- (m0 - m1)H |
手順15: (p1, q1, r1, u1, v1, w1)と(p2, q2, r2, u2, v2, w2)に基づいて、ボールの中心など、調べたい点の(x, y ,z)座標を算出する。
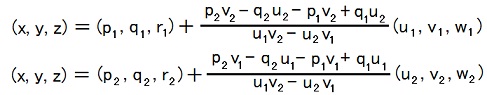
zの一致の良さで検算します。
ここまで、2つのカメラで共通のD, H, Lを使いましたが、カメラ毎に異なるD, H, Lを使っても、ここまでの方法は実質上無修正で使えます。
高度な設定方法1: D, Hの値を自分で指定する方式では、どうしてもこれらの値が不正確に成ってしまいます。そこで、プロ用の方法としては、D, Hを未知値変数のまま残しておき、xy平面上に第4代表点と第5代表点を設定し、第4代表点と第5代表点の(x, y, z)座標の両方が正確に再生されるようにD,Hの値を決める、という方法が有効だと思われます。
高度な設定方法2: y軸が撮影結果画面内の直線m=m0に正確に対応するようにするのは難しい。そこで、プロ用の方法としては、カメラの旋回角、ロール角、m0, D, Hを未知値変数のまま残しておき、xy平面上の幾つかの代表点の(x, y, z)座標の全部が正確に再生されるように未知値変数の値を決める、という方法が有効だと思われます。ただし、この方法は、当ページで説明されている計算式そのままでは実行できない(計算式の発展形を作る必要が有る)し、専用のソフトウェアを新規に作る事も必要とします。
---
実際には、選手の身体が邪魔に成って必要な位置がカメラから見えない場合に備えて、Y+型配置、Y-型配置、X+型配置、X-型配置、以上4箇所に合計4台のビデオ・カメラを設置して、それらのうちの2つから得られる撮影結果を使うのが良いだろう。
大きな大会では、念のためにz軸上に第5のビデオ・カメラも設置した方が良かろう。
異なるビデオ・カメラの向きの違いは本当は90度よりも小さい方が死角が生じ難いかもしれない。
しかし、そうすると計算がもう少し面倒に成るし、精度も少し低く成るだろう。
---
電卓と高精度計算サイトのサービスを利用して計算すると、1つの点について半日ぐらい掛かってしまったので、BASICでプログラムを作りました。
これを使うと一瞬で答えが出ます。
| 10 INPUT "D=";D 20 INPUT "H=";H 30 INPUT "L=";L 40 INPUT "M0a=";M0A 50 INPUT "M1a=";M1A 60 INPUT "N1a=";N1A 70 INPUT "N2a=";N2A 80 INPUT "M0b=";M0B 90 INPUT "M1b=";M1B 100 INPUT "N1b=";N1B 110 INPUT "N2b=";N2B 120 TA=(D-L)/H 130 SIA=(M0A-M1A)*H/(N2A-N1A)/SQR((D-L)^2+H^2) 140 SIB=(M0B-M1B)*H/(N2B-N1B)/SQR((D-L)^2+H^2) 143 TAA=SIA/SQR(1-SIA^2) 145 TAB=SIB/SQR(1-SIB^2) 150 THTA=ATN(TAA)-ATN(TA) 160 THTB=ATN(TAB)-ATN(TA) 170 INPUT "Ma=";MA 180 INPUT "Na=";NA 190 INPUT "Mb=";MB 200 INPUT "Nb=";NB 210 PA=0 220 QA=D 230 RA=H 240 UA=-L*(MA-M0A) 250 VA=(NA-N1A)*L*SIN(THTA)-(M0A-M1A)*D 260 WA=-(NA-N1A)*L*COS(THTA)-(M0A-M1A)*H 270 PB=D 280 QB=0 290 RB=H 300 UB=(NB-N1B)*L*SIN(THTB)-(M0B-M1B)*D 310 VB=L*(MB-M0B) 320 WB=-(NB-N1B)*L*COS(THTB)-(M0B-M1B)*H 330 KA=(PB*VB-QB*UB-PA*VB+QA*UB)/(UA*VB-UB*VA) 340 KB=(PB*VA-QB*UA-PA*VA+QA*UA)/(UA*VB-UB*VA) 350 XA=PA+KA*UA 360 YA=QA+KA*VA 370 ZA=RA+KA*WA 380 XB=PB+KB*UB 390 YB=QB+KB*VB 400 ZB=RB+KB*WB 410 PRINT "Xa=";XA,"Ya=";YA,"Za=";ZA 420 PRINT "Xb=";XB,"Yb=";YB,"Zb=";ZB 430 END |
PC-BASICというフリーソフトをダウンロードして使うとASIN関数が正常に機能しなかったので、143行と145行を加筆してASIN関数を使わずATN関数だけで済ませると、半日かけて出した結果と一致しました。
以下の写真はASIN関数が壊れている様子です。
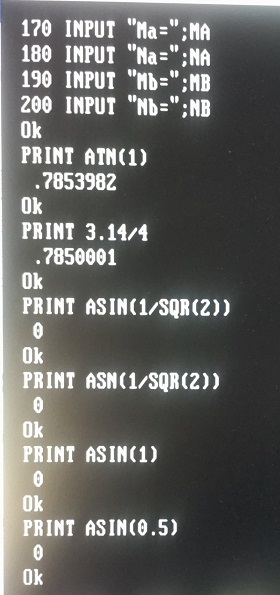 撮影2025年02月19日15時51分頃。
撮影2025年02月19日15時51分頃。PC-BASICをダウンロードした直後にもASIN関数の反応をチェックしたが、その時は正常だったので、これも集団ストーカー工作の被害だろう。
この様に写真を撮っておかなければ、「そんな事あるわけない」「お前の頭がおかしいんだ」と言われる仕掛けに成っている。
-----
以下は、以上の計算方法の根拠や導出です。
---
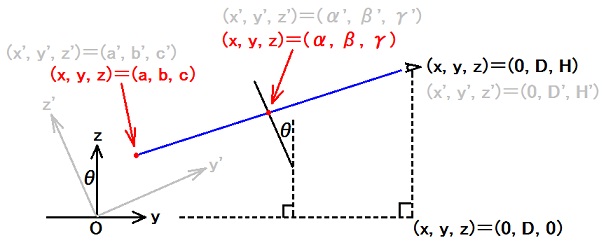
| x' = x ・・・ (0a) | y' = y cosθ + z sinθ ・・・ (0b) | z' = -y sinθ + z cosθ ・・・ (0c) |
| a' = a ・・・ (1a) | b' = b cosθ + c sinθ ・・・ (1b) | c' = -b sinθ + c cosθ ・・・ (1c) |
| α' = α ・・・ (2a) | β' = β cosθ + γ sinθ ・・・ (2b) | γ' = -β sinθ + γ cosθ ・・・ (2c) |
| 0 = 0 | D' = D cosθ + H sinθ ・・・ (3b) | H' = -D sinθ + H cosθ ・・・ (3c) |
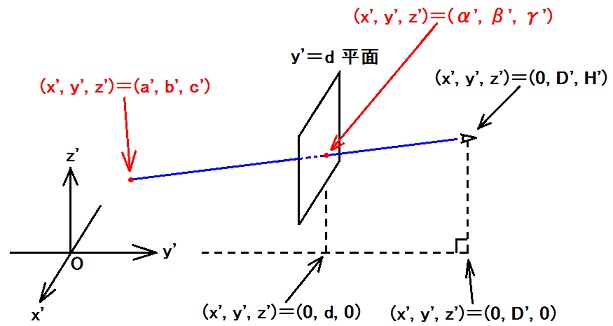
直線の方程式は、
(x', y', z') = (0, D', H') + k(a' - 0, b' - D', c' - H') ・・・ (4).
点(x', y', z') = (α', β', γ')がこの直線上にあるのだから、
(α', β', γ') = (0, D', H') + k(a' - 0, b' - D', c' - H') ・・・ (5a).
また、点(x', y', z') = (α', β', γ')はy'=d平面上にあるのだから、
β' = d ・・・ (5b).
(5a)(5b)より、
β' = D' + k(b' - D')
∴ k = (β' - D')/(b' - D') = (d - D')/(b' - D') ・・・ (6).
この結果を(5a)に代入すると、
α' = 0 + k(a' - 0) = ka' = a'(D' - d)/(D' - b') ・・・ (7a),
γ' = H' + k(c' - H') = H' - (H' - c')(D' - d)/(D' - b') ・・・ (7b).
| α' = a'(D' - d)/(D' - b') ・・・ (7a) |
| β' = d ・・・ (5b) |
| γ' = H' - (H' - c')(D' - d)/(D' - b') ・・・ (7b) |
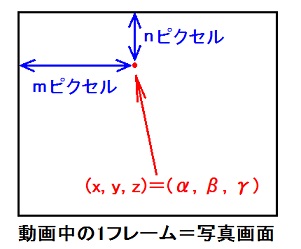
| α' = (m0 - m)ε ・・・ (8a) |
| γ' = (n0 - n)ε ・・・ (8b) |
y軸はx=0の直線だから、写真画面中にy軸はa=0の像として写っています。
(1a)(7a)(8a)から、y軸の像は直線m = m0である事が分かります ・・・ (9a)。
これによってm0の値を測定します。
d, ε, n0の値を測定する為に、x軸上の以下の2つの点に印を付け、写真画面中のそれらの像の(m, n)の値を測定し、測定結果をm1, n1とします。
| 第1代表点 | (a, b, c)=(0, 0, 0) | (a', b', c')=(0, 0, 0) ∵(1a)(1b)(1c) | (m, n)=(m0, n1) | ・・・ (9b) |
| 第2代表点 | (a, b, c)=(L, 0, 0) | (a', b', c')=(L, 0, 0) ∵(1a)(1b)(1c) | (m, n)=(m1, n1) | ・・・ (9c) |
Lの値は自分で勝手に決めます。例えばL=1メートルとか、L=1.4スネとか。
(7a)(8a)(9c)より、第2代表点について、
(m0 - m1)ε = α' = L(D' - d)/D' ・・・ (10a).
(7b)(8b)(9b)より、第1代表点について、
(n0 - n1)ε = γ' = H' - H'(D' - d)/D' ・・・ (10b).
(x', y', z')=(0, D', H')と(x', y', z')=(α', β', γ')の2点を通る直線の方程式は、
(x', y', z') = (0, D', H') + k(α' - 0, β' - D', γ' - H')
⇔ (x', y', z') = (0, D', H') + k((m0 - m)ε, d - D', (n0 - n)ε - H') ・・・ (11a)
∵(8a)(5b)(8b)
(m0 - m)ε = [L(D' - d)/D'](m0 - m)/ (m0 - m1) ・・・ (11b)
∵(10a)
(n0 - n)ε - H' = (n0 - n1)ε + (n1 - n)ε - H'
= -H'(D' - d)/D' + (n1 - n)ε ∵(10b)
= -H'(D' - d)/D' + [L(D' - d)/D'](n1 - n)/ (m0 - m1) ・・・ (11c)
∵(10a)
(11b)(11c)を使うと、(11a)は次の形に書ける。
(x', y', z') = (0, D', H') + {k(D' - d)/[D'(m0 - m1)]}(L(m0 - m), -D'(m0 - m1), -H'(m0 - m1) + L(n1 - n))
これは直線の方程式だからk(D' - d)/[D'(m0 - m1)]をkに書き換えても、表現する直線は同じである。
| (x', y', z')=(0, D', H')と(x', y', z')=(α', β', γ')の2点を通る直線の方程式 |
| (x', y', z') = (0, D', H') + k(L(m0 - m), -D'(m0 - m1), -H'(m0 - m1) + L(n1 - n)) ・・・ (12) |
一方、(0a)(0b)(0c)より、
x = x' ・・・ (0a1),
y = y' cosθ - z' sinθ ・・・ (0b1),
z = y' sinθ + z' cosθ ・・・ (0c1).
(12)を(0a1)(0b1)(0c1)にそのまま代入するんじゃなくて、方向ベクトルの部分だけを代入します。
直線が(x, y, z)=(0, D, H)を通る事は最初から分かっているからです。
-D'(m0 - m1)cosθ - [-H'(m0 - m1) + L(n1 - n)]sinθ
= (m0 - m1)(H'sinθ - D'cosθ) - (n1 - n)Lsinθ
= -(m0 - m1)D - (n1 - n)Lsinθ
= (n - n1)Lsinθ - (m0 - m1)D
-D'(m0 - m1)sinθ + [-H'(m0 - m1) + L(n1 - n)]cosθ
= -(m0 - m1)(H'cosθ + D'sinθ) + (n1 - n)Lcosθ
= -(n - n1)Lcosθ- (m0 - m1)H
| (x, y, z)=(0, D, H)と(x, y, z)=(α, β, γ)の2点を通る直線の方程式 |
| (x, y, z) = (0, D, H) + k(L(m0 - m), (n - n1)Lsinθ - (m0 - m1)D, -(n - n1)Lcosθ- (m0 - m1)H) ・・・ (13) |
| カメラ配置 | カメラの位置 | 第1代表点 | 第2代表点 | m=m0 |
| Y+型配置 | (x, y, z)=(0, D, H) | (x, y, z)=(0, 0, 0) | (x, y, z)=(L, 0, 0) | y軸 |
| X+型配置 | (x, y, z)=(D, 0, H) | (x, y, z)=(0, 0, 0) | (x, y, z)=(0, -L, 0) | x軸 |
| Y-型配置 | (x, y, z)=(0, -D, H) | (x, y, z)=(0, 0, 0) | (x, y, z)=(-L, 0, 0) | y軸 |
| X-型配置 | (x, y, z)=(-D, 0, H) | (x, y, z)=(0, 0, 0) | (x, y, z)=(0, L, 0) | x軸 |
視点と像点の2点を通る直線の方程式を
(x, y, z) = (p, q, r) + k(u, v, w)
とすると
| カメラ配置 | p | q | r | u | v | w |
| Y+型配置 | 0 | D | H | L(m0 - m) | (n - n1)Lsinθ - (m0 - m1)D | -(n - n1)Lcosθ- (m0 - m1)H |
| X+型配置 | D | 0 | H | (n - n1)Lsinθ - (m0 - m1)D | -L(m0 - m) | -(n - n1)Lcosθ- (m0 - m1)H |
| Y-型配置 | 0 | -D | H | -L(m0 - m) | -(n - n1)Lsinθ + (m0 - m1)D | -(n - n1)Lcosθ- (m0 - m1)H |
| X-型配置 | -D | 0 | H | -(n - n1)Lsinθ + (m0 - m1)D | L(m0 - m) | -(n - n1)Lcosθ- (m0 - m1)H |
2つの直線
(x, y, z) = (p1, q1, r1) + k1(u1, v1, w1) ・・・ (14a),
(x, y, z) = (p2, q2, r2) + k2(u2, v2, w2) ・・・ (14b)
は(x, y, z) = (a, b, c)で交わっているのだから、これらの直線のxy平面への射影の交点を求める
(x, y) = (p1, q1) + k1(u1, v1) ・・・ (14a'),
(x, y) = (p2, q2) + k2(u2, v2) ・・・ (14b')
という連立方程式を解けば、k1, k2の値が分かります。
| k1 = (p2v2 - q2u2 - p1v2 + q1u2)/(u1v2 - u2v1) ・・・ (15a) k2 = (p2v1 - q2u1 - p1v1 + q1u1)/(u1v2 - u2v1) ・・・ (15b) |
| (a, b, c) = (p1, q1, r1)+[(p2v2 - q2u2 - p1v2 + q1u2)/(u1v2 - u2v1)](u1, v1, w1) ・・・ (16a) and (a, b, c) = (p2, q2, r2)+[(p2v1 - q2u1 - p1v1 + q1u1)/(u1v2 - u2v1)](u2, v2, w2) ・・・ (16b) |
θの値を測定するには第3代表点を使います。
| カメラ配置 | 第3代表点 | |||
| Y+型配置 | (a, b, c)=(0, L, 0) | (a', b', c')=(0, Lcosθ, -Lsinθ) | (m, n)=(m0, n2) | ・・・(17a) |
| X+型配置 | (a, b, c)=(L, 0, 0) | (a', b', c')=(Lcosθ, 0, -Lsinθ) | (m, n)=(m0, n2) | ・・・(17b) |
| Y-型配置 | (a, b, c)=(0, -L, 0) | (a', b', c')=(0, -Lcosθ, -Lsinθ) | (m, n)=(m0, n2) | ・・・(17c) |
| X-型配置 | (a, b, c)=(-L, 0, 0) | (a', b', c')=(-Lcosθ, 0, -Lsinθ) | (m, n)=(m0, n2) | ・・・(17d) |
(n2 - n1)÷(m0 - m1)
= [(n0 - n1)ε - (n0 - n2)ε]÷[(m0 - m1)ε]
= [(第1代表点のγ') - (第3代表点のγ')]÷(第2代表点のα') ∵(8a)(8b)(9b)(9c)(17)
= {[H' - H'(D' - d)/D'] - [H' - (H' +Lsinθ)(D' - d)/(D' - Lcosθ)]}÷[L(D' - d)/D'] ∵(7a)(7b)(17a)
= [-H'(D' - d)/D' + (H' +Lsinθ)(D' - d)/(D' - Lcosθ)]÷[L(D' - d)/D']
= [-H'/D' + (H' +Lsinθ)/(D' - Lcosθ)]÷(L/D')
= (1/L)[-H' + D'(H' +Lsinθ)/(D' - Lcosθ)]
= (1/L)[H'L(cosθ)/(D' - Lcosθ) + D'L(sinθ)/(D' - Lcosθ)]
= (H'cosθ + D'sinθ)/(D' - Lcosθ)
= H/(D' - Lcosθ) ∵(3b)(3c)
= H/(D cosθ + H sinθ - Lcosθ) ∵(3b)
∴ D cosθ + H sinθ - Lcosθ = H/[(n2 - n1)÷(m0 - m1)]
∴ (D - L)cosθ + Hsinθ = H/[(n2 - n1)÷(m0 - m1)] = H(m0 - m1)/(n2 - n1).
ここでtanφ = (D - L)/Hとすれば、
sinφcosθ + cosφsinθ = {H/[(D - L)2 + H2]1/2}(m0 - m1)/(n2 - n1)
∴ sin(θ + φ) = {H/[(D - L)2 + H2]1/2}(m0 - m1)/(n2 - n1)
∴ θ = -tan-1[(D - L)/H] + sin-1[{H/[(D - L)2 + H2]1/2}(m0 - m1)/(n2 - n1)].
| θ = -tan-1[(D - L)/H] + sin-1[H(m0 - m1)/{(n2 - n1)[(D - L)2 + H2]1/2}] ・・・ (18) |
以下では、直接測定の結果と比較して検証します。
---
ホウキの柄の先端の位置座標を測定しました。

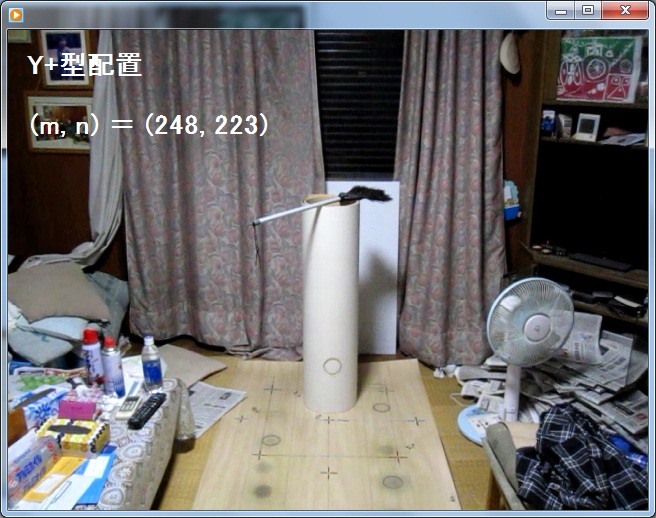
(D - L)/H = (2.4 - 0.377)/1.412 = 1.43271954674221,
H(m0 - m1)/{(n2 - n1)[(D - L)2 + H2]1/2}
= 1.412×(328 - 241)÷{(472 - 419)×√[(2.4 - 0.377)2 + 1.4122]}
= 122.844÷[53√(4.092529 + 1.993744)]
= 122.844÷130.752976474725・・・
= 0.9395120731629858・・・
θ = -tan-1[(D - L)/H] + sin-1[H(m0 - m1)/{(n2 - n1)[(D - L)2 + H2]1/2}]
≒ -55.085987555594度 + 69.969776264194度
≒ 14.8837887086度、
sinθ ≒ 0.25685935602093,
cosθ ≒ 0.96644879389677.
p1 = 0, q1 = 2.4メートル, r1 = 1.412メートル、
u1 = 0.377×(328 - 248) = 30.16メートル、
v1 ≒ (223 - 419)×0.377×0.25685935602093 - (328 - 241)×2.4 = -227.7798515350986メートル、
w1 ≒ -(223 - 419)×0.377×0.96644879389677 - (328 - 241)×1.412 = -51.43116572137987メートル、
p2 = 2.4メートル, q2 = 0, r2 = 1.412メートル、
u2 ≒ (224 - 419)×0.377×0.25685935602093 - (328 - 241)×2.4 = -227.6830155578787メートル、
v2 = -0.377×(328 - 406) = 29.406メートル、
w2 ≒ -(224 - 419)×0.377×0.96644879389677 - (328 - 241)×1.412 = -51.79551691667895メートル。
k1 = (p2v2 - q2u2 - p1v2 + q1u2)/(u1v2 - u2v1)
= (2.4×29.406 - 2.4×227.6830155578787)÷(30.16×29.406 - 227.6830155578787×227.7798515350986)
=(70.5744 - 546.4392373389089)÷(886.88496 - 51861.60348083716)
= 475.8648373389089÷50974.71852083716
= 0.0093353107412332.
a = p1 + 0.0093353107412332u1 = 0.2815529719555926メートル、
b = q1 + 0.0093353107412332v1 = 0.2736043053278904メートル、
c = r1 + 0.0093353107412332w1 = 0.9318740862070577メートル。
k2 = (p2v1 - q2u1 - p1v1 + q1u1)/(u1v2 - u2v1)
= (-2.4×227.7798515350986 + 2.4×30.16)÷(30.16×29.406 - 227.6830155578787×227.7798515350986)
= -474.2876436842366÷(886.88496 - 51861.60348083716)
= 474.2876436842366÷50974.71852083716
= 0.0093043700376758
a = p2 + 0.0093043700376758u2 = 0.2815529719556004メートル、
b = q2 + 0.0093043700376758v2 = 0.2736043053278946メートル、
c = r2 + 0.0093043700376758w2 = 0.9300753443145223メートル。
cの値の一致も悪くない、2mmぐらいズレているが。
直接測定の結果は(a, b, c) ≒ (27cm, 27cm, 92.2cm)だった。
大体一致している。
同一の被写点を2台のカメラで同時に撮影する代わりに2つの被写点を1台のカメラで異なる時刻に撮影した事と、直接測定の測定誤差が大きかった事が、直接測定の結果と計算結果が少し食い違った原因だろう。
以下は説教です。
---
私(宇田雄一)は、2辺を共有する2つの三角形の底辺の長さの比についての中学校で習う数学を使えば距離測定器を作れると自分で発想した事をキッカケとして、中学2年生(1981年)か中学3年生(1982年)の夏休みの自由研究として、距離測定器という物を作り、神辺東中学校の福本という理科の先生に褒められた。
いわゆる測距儀の簡易版です。
その頃既に当ページで発表されているビデオ判定法の萌芽が見られた、という事だ。
また、当ページで発表している数式のうちの(7a)と(7b)は、私が高校生だった時に遠近法の数学として自分で考え出した式です。
また、小学生だった頃(1970年代)に私は、木製の角材に竹筒が少しだけ被さる様に釘で結合した草野球遊びで軟球を打つ為のバットを自作した。
それを見た私の父ウダオサムは私に向かって「馬鹿だなあ、そういうのを木に竹をつぐって言うんだよ」と言ってけなした。
今インターネットで「木に竹をつぐ」を調べてみると、「前後関係や筋が通らないことを意味する慣用句です。木と竹のように性質が異なるものを継ぎ合わせることはできないことから、ちぐはぐで調和がとれていないことのたとえとして使われます」と書かれていた。
2千1桁年代に私がインターネット掲示板で空手について色々と意見交換をしていた時に「あなたの空手論はヌエ・・・であり的外れである」という意味の事を「ヌエ」という言葉を使って言われた事が有る。
今インターネットで「ヌエ」を調べてみると、「鵺、・・・、夜鳥、奴延鳥は、日本で伝承される妖怪である。・・・平家物語などに登場し、猿の顔、狸の胴体、前後の肢は虎、尾は蛇。・・・」と書かれていた。
つまり、私がウダオサムやインターネット掲示板投稿者から言われた言葉は、特にこれらが一致している事から、私(宇田雄一)の創意工夫には異質なものを継ぎ合わせる傾向が有る事を示している。
この事は、他者から言われるまで私はあまり自覚していなかった。
そして、どうですか、当ページのビデオ判定法も、異質なものを継ぎ合わせていませんか。
どこがそうかは追って考えたいが、漠然とそういう印象を私は受けます。
考えて見ました、デジタル式の画像ファイルでは長さの単位はピクセルですが、実空間では長さの単位はメートルです、両者の間に換算規則(100ピクセル=1メートルなど)は存在しません、その意味で両者は異質です。
だから、「木に竹をつぐ」と言われた話と「ヌエ・・・」と言われた話を思い出したんですよ。
発明というのは、よくよく調べてみると「この人にしてこの発明あり」と感じられる様な物でありがちなのであって、青天の霹靂の様に何の脈絡も無く突然思い浮かぶものではない。
「思い付きで物を言うな」という言葉を頻繁に目にするか耳にしてうるさい時期(何年も続いて今思い出しても脳に膠原反応が出る)が有ったが、私の発想が馬鹿の思い付きに見えたんだろうか。
大学生時代に私が量子力学のハミルトニアンのポテンシャル項としてデルタ関数形の項を試しに使ってみたのを見た鈴木公という先生が「既出のアイデアを私がカンニングしたのだ」と断定して授業で非難した事は、その発案を生む私の旧来の持ち味という物まで否定する行為でもあったという意味で非常に許し難いのである。
今思い出しても手に神経痛が出てるよ。
これは膠原反応です。
小学生時代から大学卒業後までにわたっての色々な事をここまでに書きましたが、この様に、全ての道がローマに続くぐらいに、事実というのは際限なくつながっているものです。
気に入らない部分だけを切り取って「違うんだ」と否定すると、つじつまが合わなく成ってしまうんですよ。
それは歴史の記録の破壊であって、個人の権利の侵害だけでは済まないし、多くの人にとって、もっと気に入らない物に成ると思う。
真実は小説より奇なりと言われる様に、作り話よりもホントの事の方が面白いんですよ。
ホントの事はホントの事として認めるしかない、と潔く諦める姿勢が大切である。
これが「正義に対する諦め」と私が呼ぶ態度です。
マイケル・サンデルというハーバード大学の教授は開き直って「実力主義がいけないんだ」と言い始めた。
(実力主義を否定するとは具体的にはどういう事なのか知らないから、そんな事を言うのだと思う。また、分断の原因は実力主義じゃなくて分業だと思うよ。実力主義だろうが世襲だろうが分業なら分断だよ。分業しないって言うのは大学教授って職種も無くすって事でしょ。実力主義を否定されたらほとんど「人間を返せ」に成るんですよ)
丁度私が自分の才能や能力への濡れ衣を晴らし終えた頃に、それは聞え始めた。
一体どういう事なんだ。
また私の父ウダオサムは、「お前は(東京の)大学に行ったのを境に理屈っぽく成った」なんて間違った事を言う様に成っている。
「東京に行ったのを境に理屈っぽく成った」とは、山口連続殺人放火事件の犯人である保見光成さんが言われているのと同じ台詞です。
こんな台詞で口裏を合わせて本当の事を捻じ曲げる行為が世界中で横行しているので気を付けて下さい。
大変危険な状態に成っています。
精神病冤病もそのひとつです。
私は、冤罪で凶悪犯罪の犯人に仕立て上げられたり、実際に凶悪犯罪をするように追い込まれた上でその動機は全く歪んだ物だったという事にされる恐怖を感じるんですよ。
したがって、保見光成さんはそうだったのだろうなあ、という事も分かるんです。
私は中学生の時に既に距離測定器を自分で発想して自作するほど理屈っぽい少年だったんだよ。
また、私の祖父、ウダオサムの父の名前は、宇田理一だ、「理」の字が入ってるんだよ、これ。
自分の才能や能力を証明して見せた時、謝らなければいけないのはそれを否定して来た人々であり(謝っても許しはしないけど)、証明して見せた事を謝らなければいけない、なんて言うのは、どこの理屈だ、それは。
「宇田は天才で他の人は大抵は凡人だとしたら大抵の人はどう成るんだ」という理由で「だから宇田も凡人だ」と認定したら宇田はどう成るんだ。
人はみな同じ様に尊重されなければいけないんだよ、それが法の下の平等だろうが。
それから、この問題はあまりに腹が立つので毎回言い忘れるが、私が天才でそれを存分に発揮したら他の人がどうか成るという事がもし有りましたら発表形式でお知らせ下さい。
私の目にもとまるかもしれません。
そういう事がもし有れば、間違った法則性が社会に通用しているという事ですから、それをみんなで正して行く必要が有ります。
法則性を正すべきなのであって、法則性を理由に才能を存分に発揮するのをやめさせる、才能を否定する、というのは間違ってますよね。
当ページのビデオ判定法を生んだ私による物事の狙い方を見れば、OSINT(オシント)という方法も、宇田雄一が言ってる事を聞いたり宇田雄一がやってる事を見た人が始めたのだろう、という風に感じられるのではないでしょうか。
20才台の頃に私は、物理学の研究について、教科書だけ読んでオリジナリティの高い業績を出す(論文を読んだり先発の研究に参加しなければ無理だと普通は考えられている)、という方針を口にした事が有る。
当ページのビデオ判定法を一般化すれば、GPS座標が正確に分かっている被写体が十分な個数だけ同時に複数の写真に写っていれば、それを基に、それらの写真に同時に写っている他の被写体のGPS座標も計算で分かってしまう様に出来るのではないか、と思う。
そういう計算式を作れる人って、居るんでしょ、どうせ。
これはオシントに使えるよね。
次の話題に進みます。
(11a)(11b)を見て私は、(11a)の方向ベクトル(右辺第2項)の最初の2つの成分にはD' - dという因子が入っている事に成るので、(11a)の中の(n0 - n)ε - H'という項にもD' - dという因子が入っていそうだ、と思い、その事を(11c)で確め、「やっぱりそうか!」と思いました。
方向ベクトルの最初の2つの成分にD' - dという因子が入っているならどうして第3成分にもD' - dという因子が入っていそうなのか?
それは、(12)の根拠として(12)の直前に書かれている、直線の方程式中の方向ベクトルを定数倍しても表現する直線は変わらないという道理と、そもそもこの問題では撮影結果画像だけから直線を特定できそうだからdとεは直線の方程式を導出する過程で消去されるだろうという洞察(私の自慢)によります。
そして実際、私のその予感は的中して、直線の方程式である(12)にはdもεも含まれていないわけです。
(直接測定結果との比較でk1, k2の値が非常に小さく成っているのは、その定数倍のせいで方向ベクトルがべらぼうに長いベクトルに成っている事を意味します)
この部分が、当ページで発表されているビデオ判定法の最大の見せ場です。
この展開を事前に予期したからこそ私は、このビデオ判定法の作成に着手しました。
右脳か左脳か、というステレオタイプな論評がマスコミから聞えて来るのをうるさがって、学問では右脳と左脳の両方を動員する二刀流が当たり前であると私は前々から言っていますが、本件はその良い例です。
洞察の部分が右脳的で、数式処理でεとdを消去する部分が左脳的です。
洞察の部分では映像で考えているので、エヴィデンスを示せと言われても答える事が出来ません。
これが二刀流(2脳流?)の手本なので、そっち系の若い人は真似してみて下さい。
図で考えるのが右脳的、言葉や数式で考えるのが左脳的です。
両者を同時に駆使するのではなくて、言葉や数式で進めない所は図で進み、図で進めない所は言葉や数式で進む、その後で、図で進んだ所は言葉や数式に、言葉や数式で進んだ所は図に翻訳しておき、以後はそれを早見表の様に使います。
これの典型例は、3次元ベクトル代数で外積結果の回転は回転結果の外積に等しい事が、図では明白だが数式で示すのは難しい事です。
図で進んだ後で数式に翻訳しておくと、以後は、数式だけで進む事も出来る様に成る。
さて、(D' - d)を括り出す事が出来るのではないか、と疑った時点では、(D' - d)という因子を括り出す事が出来る事をまだ証明していないわけです、当然。
それなのに、「アレが怪しいから調べてみよう」「コレが怪しいから調べてみよう」と発言すると、「根拠の無い事を言うな」「エヴィデンスを示せ」というおかしな事を言い出す行為が横行しています。
全く無根拠に怪しいと言ってるわけではなく、先述した道理と洞察を根拠として怪しいと私は言ってるわけです。
それらは証明したという意味での根拠ではありませんが、証明を試みる為の根拠としては十分です。
証明を試みる為の根拠として完成された証明を要求されたのでは、誰も証明作業を開始できないではありませんか。
もっと漠然とした長期の話としては、自分は天才だという自覚は、間違ってる場合も有るだろうけど、正しい場合も有り、ほとんどは間違いで正しい場合がどんなに希であるとしても、本当に天才ならば自分は天才だと必ず自覚するはずです。
つまり、自分を天才だと自覚する事は天才である為の必要条件だが十分条件ではない、本当に天才である事は自分を天才だと自覚する為の十分条件だが必要条件ではない、というのが私の予想です。
私が自分は天才だろうからその路線でやってみようという考えで何十年間も生きてみた結果こんな結果もあんな結果も出せたので自分は天才だった「やっぱりな」と言うのは、(11c)を見ての「やっぱりそうか!」と全く同じなんですよ。
これに対して「根拠の無い事を言うな」「エヴィデンスを示せ」と言うのと同様の態度が長年に渡って私に当てられて来た上、結果を出すと今度は一転して「何て事をしやがるんだ」という態度を当てて来る、これは絶対に許してはいけない。
先見性、予見性が無ければ何も出来ない、歩く事すら出来ないと思いますよ、したがって、先見性や予見性を否定すれば何も出来ない様に封じ込める事が出来る、それを許すな、と言ってるんです。
次の話題に進みます。
当ページに掲載されている写真を使っての計算値と直接測定結果を比較する検証の前に私は、α=0の場合に別の写真を使って同様の検証をしました。
その検証で私はまず、以下の結果を得ました。
| (15a)(16a)を使った場合 | (15b)(16b)を使った場合 |
| k1 = 0.0041925 | k2 = 0.004333 |
| a = 0.008385メートル | a = 0.008184メートル |
| b = 0.08574メートル | b = 0.147322メートル |
| c = 1.5677メートル | c = 1.57332メートル |
これを見て私は、bの値の食い違いが大き過ぎる、と思いました。
(14a')(14b')は2つの直線のxy平面への射影だから手順15に書かれている様に、(16a)(16b)を使うと(x, y) = (a, b)は自動的に一致する。
したがって、cの値が食い違うなら分かるがbの値が食い違うのは不可解だ、と私は直ぐに思いました。
2024年11月27日に2時間ほど原因を探しましたが、原因は分かりませんでした。
みなさん、間違い探しというのは、こういう物なんですよ。
間違いを探したけれど見付からなかったから間違いは無いんだという判断をする人が居ますが、それはとんでもない事です。
結果が間違っていれば必ずどこかに間違いが有るんです。
探しても探しても見付からない、それでも間違いは有るんです。
こういう経験を私は20才頃までには既に十分に積んでいたし、その後の数十年間も続けて、自分の学力を堅実にして行ったんです。
最初はp1, q1, r1, u1, v1, w1, p2, q2, r2, u2, v2, w2の値に間違いが無いか何度も見直しましたが、そうこうしているうちに、p1, q1, r1, u1, v1, w1, p2, q2, r2, u2, v2, w2の値が間違っていても(16a)(16b)を使えば(x, y) = (a, b)は自動的に一致するのだからk1の値かk2の値が必ず間違っているはずだ、という事に気付きました。
この様な考え方も大切です。
間違い探しでは、この様な考え方を色々と自分で生み出して、間違いの存在範囲を特定して行く様にしなければいけない。
ただ闇雲に探してるわけじゃないんだよ。
その意味で、間違い探しもまた勉強に成るわけです。
k1の値かk2の値が必ず間違っているはずだ、という気付きに基づいてk1とk2の計算を見直し、2024年11月28日昼12時28分頃、k1の計算式中にミスを発見しました。
それが以下の赤色数字部分です。
誤: k1 = (p2v2 - q2u2 - p1v2 + q1u2)/(u1v2 - u2v1) = (47.6 - 0 - 0 - 1324.8)/(68 - 304704) ≒ 0.0041925.
k1の計算式中のp2v2の値は、47.6平方メートルではなく本当は81.6平方メートルです。
この事も下書きに書かれています。
47.6平方メートルというのは、p2v2ではなくr2v2です。
p2の値が書かれている行の右端に書かれているr2の値をp2の値だと誤解した事が分かります。
これなんかも、絶対にそうですが、そうである事を証明なんて出来ないでしょ。
証明を必要だと過度に主張する態度は間違っている事が分かりますね。
この様にミスの原因を突き止めれば、以後は1つの行の左端から右端まで等号で式がつながっているかどうか良く確認する様に成り、同じミスはしない人間に成る。
だから、ひとつひとつのミスの原因を究明し尽くす事にも意味が有るんですよ。
このミスに気付いた時に私は「おかしいなあ、ここは何回も確認した所なんだけどなあ」といぶかりました。
この様に、何回も確認して間違いが見付からなかった場所から後で間違いが見付かる、という事も私は過去に多数回経験しました。
例えば2019年の山梨県道志村キャンプ場女児失踪事件の捜索で、何度も確認したけれど何も見付からなかった場所から後で重要な何かが見付かった場合、おかしい、そこは何度も確認した場所だから後で犯人が置きに来たに違いない、と判断するのは早合点なわけです。
袴田巌さんの事件の捜査にも有りましたよね、5点の衣類が事件から1年以上経って味噌工場の1号タンク底部から発見された、おかしい、そんな場所は事件直後に何度も調べたはずだ、という意見が。
袴田巌さんの事件は冤罪だろうと私も思うけど、探したはずだけど見付からなかったから探した時にはそこに無かった、という判断は絶対ではないわけです。
数学の勉強をまじめにする事は、人間の注意力について詳しく成り、色々な物事について事実がどうであるかを判断する時に色々な判断材料が根拠としてどの程度有効であるか有効度を見極める力を養います。
数学や物理学の学習や研究を通しての私のそういう経験の豊富さは常人の比では有りません。
それに比べて精神科医はどうでしょうか。
精神科医というのは、自分の診断が正しかったのか間違っていたのかは、究極的には死ぬまで分かりません。
どんな結果が出ても、診断が間違っていたからではなく診断以外の要因でそう成ったのだ、という風に幾らでも言い訳が出来るからです。
その点が数学では、bの値の食い違いを見れば分かる様に、「お前が間違ったんだ、言い訳は許さないぞ」という厳しい事実を突きつけられ、それによってよりいっそう判断力に磨きが掛かって行くわけです。
こんな話も昔は良く言われた事です。
間違っても間違った事がハッキリとは分からない分野よりもその点が科学は優れているんだ、という風に。
その上、精神科医の判断材料は、全部伝聞情報です。
精神医学の学理も、症例も、全部他人から聞いた話に過ぎず、自分が患者として自分の主観で「確かにこうだった」と確認した事は1つも無いわけです、ほとんどの精神科医は。
おまけに「精神病患者は自分が病気であるか否かを判断できない状態に成っている」と言うのだから、精神科医が精神病患者に成った経験を持っていたとしても自分では何も確認できない事に成ります。
この様に何を見ても何の証拠にも成らない、何を感じても何の証拠にも成らない、という性質を反証不能と言います。
精神医学の学理は反証不能なわけです。
探しても探しても間違いは見付からなくても間違いは必ず有る事などの経験を何十年も積んで来た私から見れば、「何だお前は」「お前に何が分かるんだ」と言われるべき存在に精神科医が見えるのは至極当然なわけです。
私を現実検討のプロとすれば、精神科医なんて判断のド素人なわけです。
だから、探しても探しても間違いが見付からないから精神病です、知覚過敏です、被害妄想です、潔癖症です、という判断をしてしまうんですよ、良く言って。
その優劣関係を、現実検討能力なんて言葉を振りかざして逆さまに言い掛かって来る、これはもう精神科医という資格を設置する所から犯罪は始まっている良い証拠です。
人間の注意力に詳しいという事は、現実検討能力に詳しいという事です。
人間の注意力に詳しい私に向かって何も分かってない精神科医が現実検討能力を説くなんて言うのは、いわゆる釈迦に説法です。
精神科医は現実検討の具体的な事を、ここに私が書いたレベルでは、何も知らない。
具体的な事を知らないから的外れな判断をしてしまう、というのは、社会科学では「観念論」という言葉で批判されているようです。
この観念論というのも現実検討が誤るひとつの典型的な要因なのであって、それよりも妄想の方が重要なんだなんて事は無いのである。
これで、精神異常と知能不足は別なんだ、という言い逃れへの反論が出来ていると思います。
「良く言って」というのは、善意に解釈すれば経験が足りないから間違った判断をするのだ、という意味ですが、善意に解釈するという前提を置かなければ、反証不能な似非学理を凶器として故意に冤病している、という事です。
犯人は、反証不能だから絶対に勝てる、と思って来た様ですが、反証不能というのは学理としての致命的な欠点なんですよ。
シャッター・アイランドという映画では、この点が考え落とされているせいで、反証不能な似非学理を凶器として攻撃されればお手上げである、という内容に成っているが、そんな事は無いんですよ。
反証不能な似非学理を凶器とする犯罪勢力は証拠を全て隠滅したので安心だと考えて来た様ですが、例えば数学の学習経験の中に証拠がたくさん存在し、これは隠滅できない。
ただし、何度も確認したのでおかしい、という判断も、単に何度も確認したというだけでなく、その確認が特別な特徴を持っている、確認した人がその確認に特別な実感を持っている場合には、もう少し尊重すべきです。
そういう機微を無視する事も、ガサツという言葉で批判される態度です。
また、数学の勉強ででなくても良いけど、何かの専門分野に真剣に打ち込んで、そこから判断の機微を教訓として引き出す、という事を、一部の才能の有る人だけしかやっていない事が、世の中を危うくしていて、そこが集団ストーカーなどに付け込まれているので、気を付けて欲しい。
精神科医だけでなく、人から指導されながらする学習でも、独学に比べると、ここまでで私が指摘した様な能力が育ちません。
独学を散々にケナス人は、こういう事を考え落としている。
右脳・左脳二分法の話と似た例として、天才・努力二分法の話もマスコミから聞えて来る事が多く、とてもうるさい。
そういう話においては、天才というものが不当に貶められる傾向が有るからだ。
ここまでで私が実例を示した様に、才能が有るというのは物事に臨む姿勢・態度が優れている、という事なんですよ。
受けるべき説教を自分で考え出す事が出来たり、見逃さない、それが「才能が有る」という事です。
したがって、努力を怠る人には才能は無いんだよ。
それなのに、マスコミから聞えて来る天才・努力二分法の話は、どれも、天才が勝つか努力が勝つか、という話だし、大抵は、努力は天才に勝つんだ、という話に成ってる。
それは、私に言わせれば、勝った人(天才ではなく努力家だと言われている人)の方が本当は才能が優れていた、という事なんだよ。
「強い方が勝つんじゃない、勝った方が強いんだ」という言葉も出所は私じゃないかと思うんだけど、この言葉に倣って言うと、「天才は、頭が良いんじゃない、頭の使い方が良いんだ」という事に成ろう。
また、文系・理系という二分法も有る。
これは、二分するのが悪いとは言わないけど、これも、文系は人間ならではの大切な事を担当し、理系は物や自然を相手にするから下等である、という価値観を遠回しに表現して来る所がとてもうるさい。
社会階級が大体、文系は雇用者(管理職)、理系は被雇用者(労働者)という風に成っていて、これは、軍事についての文民統制の原則も本質的には同じである。
理科しか勉強して来なかった人と社会科しか勉強して来なかった人のどちらかを選べと言われれば、管理職の場合、社会科しか勉強して来なかった人を選ぶ方が無難だと私も思う。
軍人が政治的にも強く成り過ぎたら不幸な結果が生じた事への反省というのも妥当だと思う。
しかし、それらは、最悪の事態を回避しているに過ぎず、最悪未満の弊害は大きいし、ひょっとすると最悪級の事態も既に何件も発生しているのかもしれない。
国際政治学者の三浦瑠麗さんは、安易に出兵してしまうのは文民統制のせいだ、と言っている。
これは、出兵させても自分が血を流すわけではない人が出兵の決断をしている事の欠点を指摘する意見です。
また、もっと感覚的に、ジャイアンが自分の暴力を背景としてのびたに偉そうにする事よりも、のびたが他人の暴力を背景としてジャイアンに偉そうにする事の方が醜悪である、という構図も見ておかねばならないだろう。
理系的な能力が欠けていれば人や社会への研究や理解が不十分に成る、という事を、εとdの消去の背景に洞察が有った事から、感じ取って欲しい。
つまり、εとdの消去は、知恵の輪を触っていると良く分からないけど外れたよ、といった事ではなく、そもそもこの問題はどういう問題だからどう成るはずだ、という洞察の下で行なわれている、理系の学問のそういう特徴を文系の人は無いと誤解してませんでしたか、という事なんです。
そういう種類の洞察は、社会を研究したり理解したりする時にも必要で、そういう種類の洞察を生み得るヒントに成る成功例や失敗例を理系の学問はたくさん蓄積して持ってますよ、それらは文系の人からは出て来ないでしょう。
宇田経済学@持論@学問で私は、
(~までに買うつもりの量) ≦ (~までに売るつもりの量) + (現在持っているおカネ)
という式の全員分の合計を考えれば、
(~までに買うつもりの量の全員分の合計) ≦ (~までに売るつもりの量の全員分の合計)
が保証されない、おカネは詐欺である、という事を指摘しています。
この様な思考法は、過去に私以外の誰からも出て来なかった、特に文系の人からは出て来得ない物でしょう。
εとdの消去では、細部が決まらなくても全体としては決まる、という考え方をしています。
この時には私は電気力学の繰り込みを連想していたので、繰り込みもヒントに成っていたかもしれない。
また、数学のトポロジーという分野は全体の大づかみな特徴だけを問題にします。
この様な数学や物理学の学習や研究の経験は、宇田経済学の様な思考のヒントに成っています。
数学や物理学を学べば誰でも社会の研究に役立つヒントを得られるというものでは無いけれど、数学や物理学を勉強して来なかったら私でも宇田経済学の様な思考は出来なかったです。
次の話題に進みます。
bの値の食い違いの原因となるミスを発見して訂正したら、(a, b)の値は一致する様に成りました。
しかし今度は、cの値と素朴直接測定の結果が大きく食い違う様に成りました。
| (15a)(16a)を使った場合 | (15b)(16b)を使った場合 | 素朴直接測定の結果 | |
| c | 1.563236メートル | 1.57332メートル | 150cm |
一難去ってまた一難です。
こういう時は膠原反応相当のダメージが心身に生じます。
集団ストーカー工作は、自由状態でも生じるその様なダメージに目を付けて、それを人工的に生じさせようと狙っているだろう。
自由状態の場合は、ここで無理をしない様に努めるのが賢明です。
この様に、ミス訂正という物は、探しても探してもミスを見付ける事が出来ないだけでなく、直しても直しても答えが合わない=まだ他にミスが残っている物です。
2024年11月28日20時頃、夕食後休憩中に、原因が思い当たった。
写真撮影でカメラをうつむかせた事が原因だろう。
つまり、α=0の場合の計算式を使ったが、カメラの設置状況はα>0だった、だから計算値と素朴直接測定結果が食い違ったのだ。
分かってしまえば全く間抜けな話ですが、気付くまでに随分と時間が掛かってますよね。
これも、そういう物なんですよ。
気付くまでは、そもそもαというパラメータの存在に気付いてない、「他に一体何が有ると言うんだ、もう全部やったぞ、あ、そうか、へ?カメラの俯仰なんて関係あるっけ?有るに決まってるじゃん」という風に成ったわけです、新しい事をやる時って、人間の脳ってそのぐらい馬鹿なんですよ、それがホントの事です。
こういう事は経験した者にしか分からない。
しかし、このミスを訂正した(カメラをうつむかせず再撮影した)ら計算結果と素朴直接測定結果は大体一致する様に成りました。
その事も下書きに書かれています。
ミスを2つ直すだけで正解に到達したというのはまだ良い方だ、と考えなければいけない。
次の話題に進みます。
近年、反グローバル主義、グローバル・エリートへの批判という物が高まっています。
いかがでしょうか?当ページで私が提供しているようなノウハウを生み出す人や仕事は世の中に必要ないとあなたはお考えでしょうか?
そんな事は無いと思うんですよ、私は。
私は自分をエリートではなく天才と位置付けていますが、私が思うには、グローバル主義やエリートの概念が間違ってるんではなくて、その内容が劣化して来ている、利権化して来ている、だからいけない、という事では無いだろうか。
滅多に居ない特別に優れた能力を持った人にその能力を発揮してもらう事は世の中にとって必要である、という法則は、どんな時代でも常に成り立つ、と思うんだけど。
「どんな事が有っても暴力は許されない」と主張する種類の人が「証明を開始するためには証明が完了している事が必要である」という意味で「エヴィデンスを示せ」と言う様なおかしな意見を、「この意見には逆らえませんよ」「逆らえば失職させるなどの不利益を与えます(暴力で制裁します)よ」といった調子で言う近年の倒錯した風潮は、グローバル・エリートのチャンネルを通って世界中に行き渡っている様に私は感じます。
日本で言うと、ドラゴン桜なんてテレビ番組が放送されていた頃には、既に異変が生じていたんだろうなあ、と思う。
しかし、2020年09月に日本学術会議候補者の任命を菅義偉内閣総理大臣が拒否した時に色々と耳に入って来た日本学術会議の実態は、日本学術会議が利権化している事を示していたので、エリートという地位が利権化してしまっているという問題は、最近生じた物ではなく昔から続いている事なのだろう。
実力主義を否定するって、こういうのを肯定する事なんですけど、マイケル・サンデルさんは、どうお考えなのでしょうか。
最初にエリート職位を設立して能力試験の結果に基づいて登用を行なうと、その結果が華々しい為に次は、自分もそういう風に成りたいという人が出て来る、そうすると今度は、個人として能力が高い人ではなく社会的に力の強い人がエリート職に就く様に成る、次第にエリート職位は間接的な意味も含めてカネで買う事しかできない地位に成って行き、エリート職から出力される指導がどんどん劣化して行く。
違うかもしれないけど、この様なスケールで問題を詮索しないと、頭がぶよぶよの人ばかりに成ってしまったグローバル・エリートという怪奇現象を解明して正す事は出来ない。
| 下書き |