
since 2003
イレコナビ サイトマップ
以下の図は、私が高校生だった時に自分で考え出した遠近法の計算式です。
学問的なオリジナリティーは有りません。
程度の問題じゃないんだけど、この程度の事では、学問的に何か新しい事を考え出したうちには入らない。
けれど、スポーツの試合のビデオ判定には、革命的な進歩をもたらすかもしれない。
その時には、しっかり私の名前を冠して下さい、宇田雄一式ビデオ判定(宇田作品番号=UWV20241123)という風に。
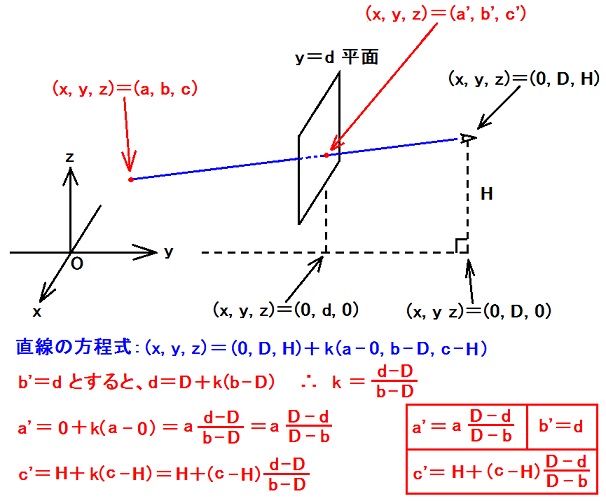
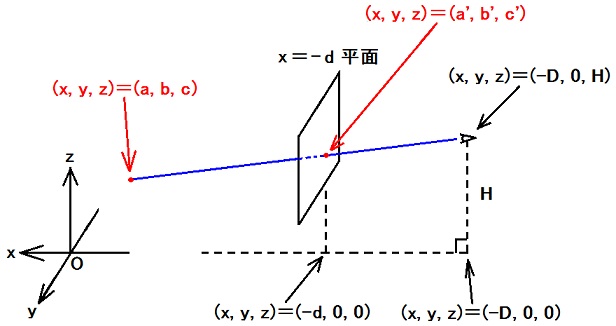
写真撮影の結果画像はy=d平面上の画像だと考えられるが、(a', c')と(m, n)の関係は共通の定数(m0, n0)と縮尺εの分だけ不定です。
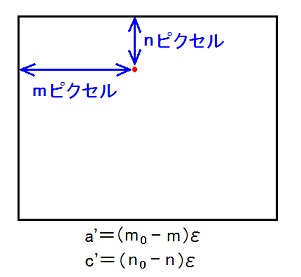
m0を求めるには、m=m0の時にa=0に成る事を使います。
a = 0 ⇔ a' = 0 ⇔ m = m0.
写真内にy軸が直線m = m0として写っている。
これを確認する事によって、m0の値を知ります。
m0の値が分かれば、xy平面内のどれか1つの点のmの値を確認する事によって、εの値を求める事ができます。
例えば、(a, b, c) = (1メートル, 0, 0)の場合m=m1だとします。
(m0 - m1)ε = a' = (1メートル)×(D - d)/D
∴ ε = (1メートル)×(D - d)/[D(m0 - m1)]
最後にn0の値を求めるには、xy平面内のどれか1つの点のnの値を確認すればよい。
例えば、(a, b, c) = (0, 0, 0)の場合n=n1だとします。
(n0 - n1)ε = c' = H - H(D - d)/D = Hd/D
∴ n0 = Hd/(Dε) + n1.
| 写真画像の特徴 | 結論 |
y軸が直線m=m0として写っている。 (a, b, c) = (1メートル, 0, 0)ならばm=m1である。 (a, b, c) = (0, 0, 0)ならばn=n1である。 |
ε = (1メートル)×(D - d)/[D(m0 - m1)], n0 = Hd/(Dε) + n1. |
(x, y, z) = (0, D, H) + k'(a' - 0, d - D, c' - H).
⇔ (x, y, z) = (0, D, H) + k'((m0 - m)ε, d - D, (n0 - n)ε - H)
ここから私が自慢したい展開に成ります。
まず、ε(D - d)は決まるけどεとdは別々には定まらない、それでも、直線の方程式は1つに決まるだろう、という事を見抜きます。
こういう洞察が出来る事が、数学の才能の1つです。
これは、決して最高級の洞察ではないし、私以外の人は誰も出来ない洞察でもないけれど、相似な三角形や因数分解を偶然見付ける能力などよりは高級な能力です。
理科系の能力を、機械がやる様な事をやる能力だとして蔑む文科系の人は、こういう事を想像だにしていないのではないでしょうか。
全部あわせるとどう成るかを考える事によって、局所では尻尾を出さない経済制度の不正な特徴を暴いている宇田経済学@持論@学問では、私のこの様な能力が発揮されており、人文系の勉強をやっただけでは社会について満足な研究が出来ない事が分かります。
| ちょっとゴメン、丁度良い例が出て来たので、別のページに書いた話について、ここで説明させて下さい。 そうしないと、直ぐ忘れてしまうんだよ。 26日@2024年09月@日記に私は「私への集団ストーカー工作を目的に淀電子社屋が私の自宅に密着させて新築された、という1件だけを私から言われても、本当にそうなんだと分かる人は少ないでしょう。分かった人は、本当に分かったのではなく判断力が足りないから分かった気に成った、と考えるべきでしょう。過去に私の言い分に納得の意を表した人を間近で見ながら、これは1人分と考えるわけには行かないな、と判断した事が何度も有りましたが、それはそういう意味です。ガス漏れ警報機が鳴った時に、鳴ったのがガス漏れ警報機である事をしっかり確認できなければ、それをガス漏れの証拠として使えない、みたいな理屈です」と書いています。 「ε(D - d)は決まるけどεとdは別々には定まらない、それでも、直線の方程式は1つに決まるだろう」と私が発言した時に、その場に居合わせた友人が、「おう、決まろう」とコメントした場合、そういう感じ(=ホントに分かって言ってるのか疑わしい)です。 実際に本件でそういう事が有ったわけじゃあないけど、別件では過去に複数回あったんだよ。 |
だから、k'((m0 - m)ε, d - D, (n0 - n)ε - H)は、(D -d)を括り出してk'(D - d)(・・・, ~, ***)という形に書けるのではないか、と疑います。
そこで、(n0 - n)ε - Hを詳しく調べてみる事にしましょう。
(n0 - n)ε - H = Hd/D + n1ε - nε - H
= H(d - D)/D + (n1 - n)ε
= H(d - D)/D + (n1 - n)×(1メートル)×(D - d)/[D(m0 - m1)]
やっぱりだ、(n0 - n)ε - Hにも(D - d)という因子が入っていた。
ついでの話ですが、(D - d)を括り出す事が出来るのではないか、と疑った時点では、(D - d)という因子を括り出す事が出来る事をまだ証明していないわけです、当然。
それなのに、「アレが怪しいから調べてみよう」「コレが怪しいから調べてみよう」と発言すると、「根拠の無い事を言うな」「エヴィデンスを示せ」というおかしな事を言い出す行為が横行しています。
全く無根拠に怪しいと言ってるわけではなく、私が自慢している洞察やk'((m0 - m)ε, d - D, (n0 - n)ε - H)の中の(m0 - m)εにもd - Dにも(D - d)という因子が入っている事、これらを根拠として怪しいと言ってるわけです。
それらは証明したという意味での根拠ではありませんが、証明を試みる為の根拠としては十分です。
証明を試みる為の根拠として完成された証明を要求されたのでは、誰も証明作業を開始できないではありませんか。
話を元に戻します。
k'((m0 - m)ε, d - D, (n0 - n)ε - H)
= k'(D - d)・((1メートル)×(m0 - m)/[D(m0 - m1)], -1, -H/D + (1メートル)×(n1 - n)/[D(m0 - m1)])
= k'{(D - d)/[D(m0 - m1)]}・((1メートル)×(m0 - m), -D(m0 - m1), -H(m0 - m1) + (1メートル)×(n1 - n))
これは直線の方程式の中の1つの項なんだから、パラメータをk'から
k'' = k'(D - d)/[D(m0 - m1)]
に変更しても、表現している直線は変わりません。
| y=d平面上の点(x, y, z)=(a', d, c')と(x, y, z)=(0, D, H)を通る直線の方程式 |
| (x, y, z) = (0, D, H) + k''((1メートル)×(m0 - m), -D(m0 - m1), -H(m0 - m1) + (1メートル)×(n1 - n)) |
私が自慢したかった展開は、ここまでです。
同じ姿勢を2方向から写真撮影すれば、その姿勢での身体の各部位の(x, y, z)を知る事が出来ると考えられます。
その為には、カメラがx軸の真上にある場合などについても、直線の方程式を求めておく必要が有ります。
| Y+ 型 配 置 |
 |
| X+ 型 配 置 |
 |
| Y- 型 配 置 |
 |
| X- 型 配 置 |
 |
| Y+ 型 配 置 |
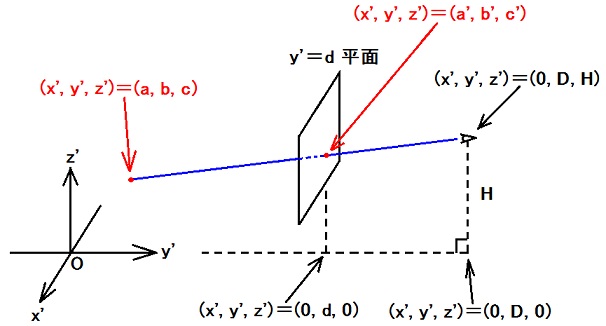
既に得られている計算結果を他のカメラ配置で利用する為に、座標軸の名前をx, y, zではなくx', y', z'としておきます。 --- a'=[m0(Y+) - m(Y+)]ε(Y+), b'=d, c'=[n0(Y+) - n(Y+)]ε(Y+). --- y'軸が直線m(Y+)=m0(Y+)として写っている。 (a, b, c) = (1メートル, 0, 0)ならばm(Y+)=m1(Y+)である。 (a, b, c) = (0, 0, 0)ならばn(Y+)=n1(Y+)である。 --- ε(Y+) = (1メートル)×(D - d)/[D(m0(Y+) - m1(Y+))], n0(Y+) = Hd/[Dε(Y+)] + n1(Y+). --- y'=d平面上の点(x', y', z')=(a', d, c')と(x', y', z')=(0, D(Y+), H(Y+))を通る直線の方程式は、 (x', y', z') = (0, D(Y+), H(Y+)) + k(Y+)((1メートル)×(m0(Y+) - m(Y+)), -D(m0(Y+) - m1(Y+)), -H(m0(Y+) - m1(Y+)) + (1メートル)×(n1(Y+) - n(Y+))). |
| X+ 型 配 置 |
x=y', y=-x', z=z'として、Y+型配置の計算結果を使います。 --- a'=d, b'=-[m0(X+) - m(X+)]ε(X+), c'=[n0(X+) - n(X+)]ε(X+). --- x軸が直線m(X+)=m0(X+)として写っている。 (a, b, c) = (0, -1メートル, 0)ならばm(X+)=m1(X+)である。 (a, b, c) = (0, 0, 0)ならばn(X+)=n1(X+)である。 --- ε(X+) = (1メートル)×(D - d)/[D(m0(X+) - m1(X+))], n0(X+) = Hd/[Dε(X+)] + n1(X+). --- x=d平面上の点(x, y, z)=(d, b', c')と(x, y, z)=(D(X+), 0, H(X+))を通る直線の方程式は、 (x, y, z) = (D(X+), 0, H(X+)) + k(X+)(-D(m0(X+) - m1(X+)), -(1メートル)×(m0(X+) - m(X+)), -H(m0(X+) - m1(X+)) + (1メートル)×(n1(X+) - n(X+))). |
| Y- 型 配 置 |
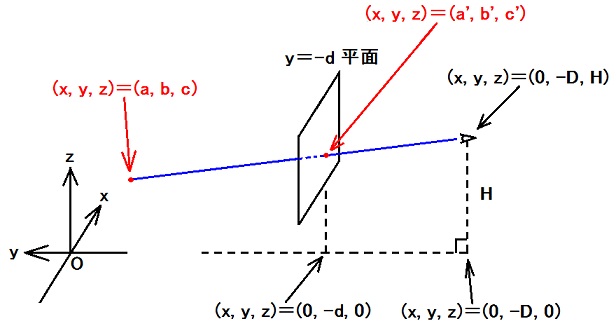
x=-x', y=-y', z=z'として、Y+型配置の計算結果を使います。 --- a'=-[m0(Y-) - m(Y-)]ε(Y-), b'=-d, c'=[n0(Y-) - n(Y-)]ε(Y-). --- y軸が直線m(Y-)=m0(Y-)として写っている。 (a, b, c) = (-1メートル, 0, 0)ならばm(Y-)=m1(Y-)である。 (a, b, c) = (0, 0, 0)ならばn(Y-)=n1(Y-)である。 --- ε(Y-) = (1メートル)×(D - d)/[D(m0(Y-) - m1(Y-))], n0(Y-) = Hd/[Dε(Y-)] + n1(Y-). --- y=-d平面上の点(x, y, z)=(a', -d, c')と(x, y, z)=(0, -D(Y-), H(Y-))を通る直線の方程式は、 (x, y, z) = (0, -D(Y-), H(Y-)) + k(Y-)(-(1メートル)×(m0(Y-) - m(Y-)), D(m0(Y-) - m1(Y-)), -H(m0(Y-) - m1(Y-)) + (1メートル)×(n1(Y-) - n(Y-))). |
| X- 型 配 置 |
x=-y', y=x', z=z'として、Y+型配置の計算結果を使います。 --- a'=-d, b'=[m0(X-) - m(X-)]ε(X-), c'=[n0(X-) - n(X-)]ε(X-). --- x軸が直線m(X-)=m0(X-)として写っている。 (a, b, c) = (0, 1メートル, 0)ならばm(X-)=m1(X-)である。 (a, b, c) = (0, 0, 0)ならばn(X-)=n1(X-)である。 --- ε(X-) = (1メートル)×(D - d)/[D(m0(X-) - m1(X-))], n0(X-) = Hd/[Dε(X-)] + n1(X-). --- x=-d平面上の点(x, y, z)=(-d, b', c')と(x, y, z)=(-D, 0, H)を通る直線の方程式は、 (x, y, z) = (-D(X-), 0, H(X-)) + k(X-)(D(m0(X-) - m1(X-)), (1メートル)×(m0(X-) - m(X-)), -H(m0(X-) - m1(X-)) + (1メートル)×(n1(X-) - n(X-))). |
2つの異なるカメラでの撮影結果から直線の方程式が2つ得られますが、この2つの方程式から直線の交点の座標を求めれば、それが(x, y, z)=(a, b, c)です。
一般に、2つの直線の方程式:
(x, y, z)=(p1, q1, r1)+k1(u1, v1, w1),
(x, y, z)=(p2, q2, r2)+k2(u2, v2, w2)
の連立方程式を解いて2つの直線の交点を求めるには、例えば、まず最初の2成分だけ考えて
(p1, q1)+k1(u1, v1)=(x, y)=(p2, q2)+k2(u2, v2)、
を解いてk1とk2の値を求め、その結果を
(x, y, z)=(p1, q1, r1)+k1(u1, v1, w1)または(x, y, z)=(p2, q2, r2)+k2(u2, v2, w2)に代入して交点の座標を得る方法が使えます。
両者が一致するかどうかを確認する事は、検算として有効です。
この方法では、まず2つの直線のxy平面への射影の交点を求めた事に成ります。
公式を作っておきます。
(p1, q1)+k1(u1, v1)=(p2, q2)+k2(u2, v2)
⇔ p1 + k1u1 = p2 + k2u2 and q1 + k1v1 = q2 + k2v2
⇔ (p1 + k1u1)v2 = p2v2 + k2u2v2 and (q1 + k1v1)u2 = q2u2 + k2v2u2
⇔ p1 + k1u1 = p2 + k2u2 and (p1 + k1u1)v2 - (q1 + k1v1)u2 = p2v2 - q2u2 ・・・ k2を消去した
⇔ p1 + k1u1 = p2 + k2u2 and (u1v2 - v1u2)k1 = p2v2 - q2u2 - p1v2 + q1u2
⇔ p1 + k1u1 = p2 + k2u2 and k1 = (p2v2 - q2u2 - p1v2 + q1u2)/(u1v2 - v1u2)
⇔ k2 = (p1 - p2)/u2 + k1u1/u2 and k1 = (p2v2 - q2u2 - p1v2 + q1u2)/(u1v2 - v1u2)
⇔ k2 = (p1 - p2)(u1v2 - v1u2)/[u2(u1v2 - v1u2)] + u1(p2v2 - q2u2 - p1v2 + q1u2)/[u2(u1v2 - v1u2)]
and k1 = (p2v2 - q2u2 - p1v2 + q1u2)/(u1v2 - v1u2)
⇔ k2 = (-p1v1u2 + p2v1u2 - q2u1u2 + q1u1u2)/[u2(u1v2 - v1u2)]
and k1 = (p2v2 - q2u2 - p1v2 + q1u2)/(u1v2 - v1u2)
⇔ k1 = (p2v2 - q2u2 - p1v2 + q1u2)/(u1v2 - v1u2) and k2 = (-p1v1 + p2v1 - q2u1 + q1u1)/(u1v2 - v1u2)
この結果は、逆行列を使うと、もっと簡単に求める事が出来ます。
この結果を代入すると、以下の公式が得られます。
| (a, b, c) = (p1, q1, r1)+[(p2v2 - q2u2 - p1v2 + q1u2)/(u1v2 - u2v1)](u1, v1, w1), (a, b, c) = (p2, q2, r2)+[(p2v1 - q2u1 -p1v1 + q1u1)/(u1v2 - u2v1)](u2, v2, w2) |
| p | q | r | u | v | w | |
| Y+型配置 | 0 | D | H | (1メートル)×(m0 - m) | -D(m0 - m1) | -H(m0 - m1) + (1メートル)×(n1 - n) |
| X+型配置 | D | 0 | H | -D(m0 - m1) | -(1メートル)×(m0 - m) | -H(m0 - m1) + (1メートル)×(n1 - n) |
| Y-型配置 | 0 | -D | H | -(1メートル)×(m0 - m) | D(m0 - m1) | -H(m0 - m1) + (1メートル)×(n1 - n) |
| X-型配置 | -D | 0 | H | D(m0 - m1) | (1メートル)×(m0 - m) | -H(m0 - m1) + (1メートル)×(n1 - n) |
試しに、ここまでで作り上げた計算方法を、実際の写真に適用してみましょう。

以下の写真は、AFS基本姿勢をY+型配置で撮影した結果です。

以下の写真は、AFS基本姿勢をX+型配置で撮影した結果です。

本当は、同一の被写体をY+型配置のカメラとX+型配置のカメラで同時に撮影しなければいけないが、それが出来なかったので、Y+型配置の撮影後、90度だけ違う向きに立ち直して、同じ位置の同じカメラでX+型配置の撮影を行なった。
したがって、異なる時刻に正確に同じ姿勢を作るのは難しい分だけ、計算結果に矛盾が出るだろう。
p1 = 0, q1 = 2.4メートル, r1 = 1.4メートル,
u1 = (1メートル)×(336 - 334) = 2メートル,
v1 = -(2.4メートル)×(336 - 106) = -552メートル,
w1 = -(1.4メートル)×(336 - 106) + (1メートル)×(455 - 93) = 40メートル,
p2 = 2.4メートル, q2 = 0, r2 = 1.4メートル,
u2 = -(2.4メートル)×(336 - 106) = -552メートル,
v2 = -(1メートル)×(336 - 370) = 34メートル,
w2 = -(1.4メートル)×(336 - 106) + (1メートル)×(455 - 93) = 40メートル。
誤: k1 = (p2v2 - q2u2 - p1v2 + q1u2)/(u1v2 - u2v1) = (47.6 - 0 - 0 - 1324.8)/(68 - 304704) ≒ 0.0041925.
誤: a ≒ p1 + 0.0041925×u1 = 0.008385メートル。
誤: b ≒ q1 + 0.0041925×v1 = 0.08574メートル。
誤: c ≒ r1 + 0.0041925×w1 = 1.5677メートル。
k2 = (p2v1 - q2u1 -p1v1 + q1u1)/(u1v2 - u2v1) = (-1324.8 - 0 - 0 + 4.8)/(68 - 304704) ≒ 0.004333.
a ≒ p2 + 0.004333×u2 = 0.008184メートル。
b ≒ q2 + 0.004333×v2 = 0.147322メートル。
c ≒ r2 + 0.004333×w2 = 1.57332メートル。
従がって、Y+型配置の撮影結果で決まる直線を使った場合と、X+型配置の撮影結果で決まる直線を使った場合で、鼻頂のy座標に食い違いが見られるが、x座標とz座標は良く一致している。
公式を作る時に、まずxy平面への射影の交点を求めたので、(a, b)は一致するはずです。
だから、c(z座標)が一致しないのなら分かるが、b(y座標)が一致しないのは不可解です→原因調査中。
2024年11月27日に2時間ほど調査したが、原因は分からなかった。
たとえp1, q1, r1, u1, v1, w1, p2, q2, r2, u2, v2, w2の値が誤りだったとしても、
k1 = (p2v2 - q2u2 - p1v2 + q1u2)/(u1v2 - u2v1)
and k2 = (p2v1 - q2u1 -p1v1 + q1u1)/(u1v2 - u2v1)
ならば必ず、q1 + k1v1 = q2 + k2v2 が成り立ちます。
だから不可解なんです。
みなさん、間違い探しというのは、こういう物なんですよ。
間違いを探したけれど見付からなかったから間違いは無いんだという判断をする人が居ますが、それはとんでもない事です。
結果が間違っていれば必ずどこかに間違いが有るんです。
こういう経験を私は何十年も積んで学力を堅実にして行ったんです。
それを、他人と交わらなければひとりよがりに成って学力は不確かなものに留まる、と言って馬鹿にされて来たわけです。
他人と仲良くしていれば、こういう経験を積めるもんですかねえ。
もっと調査します。
2024年11月28日昼12時28分頃、ミスを発見しました。
k1の計算式中のp2v2の値は、47.6ではなく81.6です。
おかしいなあ、ここは何回も確認した所なんだけどなあ。
こういう事も過去に多かった。
集団ストーカー工作で改ざんされた可能性も有るけど、これは私の見落としだと思う。
例えば2019年の山梨県道志村キャンプ場女児失踪事件の捜索で、何度も確認したけれど何も見付からなかったはずの場所から後で重要な何かが見付かった場合、おかしい、そこは何度も確認した場所だから後で犯人が置きに来たに違いない、と判断するのは早合点なわけです。
数学の勉強をまじめにする事は、人間の注意力について詳しく成り、色々な物事について事実がどうであるかを判断する時に色々な判断材料が根拠としてどの程度有効であるかを見極める力を養います。
何度も確認したのでおかしい、という判断は、単に何度も確認したというだけでなく、その確認が特別な特徴を持っている、確認した人がその確認に特別な実感を持っている場合にしか、妥当しません。
そういう機微を無視する事をガサツと言うんですよ。
知覚過敏だの被害妄想だの潔癖症だのという評価を安易に付ける事を私が厳しく批判するのは、それらがガサツな論理で行なわれるからです。
また、数学の勉強ででなくても良いけど、何かの専門分野に真剣に打ち込んで、そこから判断の機微を教訓として引き出す、という事を、一部の才能の有る人だけしかやっていない事が、世の中を危うくしていて、そこが集団ストーカーなどに付け込まれているので、気を付けて欲しい。
訂正します。
正: k1 = (p2v2 - q2u2 - p1v2 + q1u2)/(u1v2 - u2v1) = (81.6 - 0 - 0 - 1324.8)/(68 - 304704) ≒ 0.0040809
正: a ≒ p1 + 0.0040809×u1 = 0.0081618メートル。
正: b ≒ q1 + 0.0040809×v1 = 0.1473432メートル。
正: c ≒ r1 + 0.0040809×w1 = 1.563236メートル。
k1で計算した場合とk2で計算した場合で、aとbは完全一致、cも大体同じぐらいに成っている、これでよし。
過去にもっと素朴な方法で測定した時の結果は、以下のごとくです。
a ≒ -1.0cm, b ≒ 13.5cm, c ≒ 150cm.
この結果と比較して、当ページの計算結果はcが6~7cmも大きい。
この事は、当ページの計算方法が間違っている可能性を、感じさせる。
今後さらに検証したい。
2024年11月28日20時頃、夕食後休憩中に、原因が思い当たった。
写真撮影でカメラをうつむかせた事が原因だろう。
2024年11時29日昼12時頃、カメラをうつむかせず光軸を水平にして再撮影した。
その結果が以下です。



p1 = 0, q1 =2.4メートル, r1 = 0.66メートル,
u1 = (1メートル)×(331 - 336) = -5メートル,
v1 = -2.4メートル×(331 - 77) = -609.6メートル,
w1 = -0.66メートル×(331 - 77) + (1メートル)×(445.5 - 49) = 228.86メートル,
p2 = 2.4メートル, q2 = 0, r2 = 0.66メートル,
u2 = -2.4メートル×(331 - 77) = -609.6メートル,
v2 = -1メートル×(331 - 373) = 42メートル,
w2 = -0.66メートル×(331 - 77) + (1メートル)×(445.5 - 64) =213.86.
k1 = (p2v2 - q2u2 - p1v2 + q1u2)/(u1v2 - u2v1) = (100.8 - 0 - 0 - 1463.04)/(-210 - 371612.16) ≒ 0.0036637,
a = p1 + k1u1 ≒ -0.0183185メートル,
b = q1 + k1v1 ≒ 0.1666メートル,
c = r1 + k1w1 ≒ 1.4985メートル.
k2 = (p2v1 - q2u1 -p1v1 + q1u1)/(u1v2 - u2v1) = (-1463.04 - 0 - 0 - 12)/(-210 - 371612.16) ≒ 0.003967,
a = p2 + k2u2 ≒ -0.0182832メートル,
b = q2 + k2v2 ≒ 0.166614メートル,
c = r2 + k2w2 ≒ 1.50838メートル.
bの値が少し大きめに出ているが、写真を見れば分かる様に、これは実際に私が上体の傾きを変えてしまったからだろう。
したがって、宇田雄一式ビデオ判定の正しさはここまでで実証された、と言って良いだろう。
今後、カメラをうつむかせた場合の公式も作ってみたい。
光軸の向きが水平と角αだけ違う場合、以下の設定が出発点と成ります。
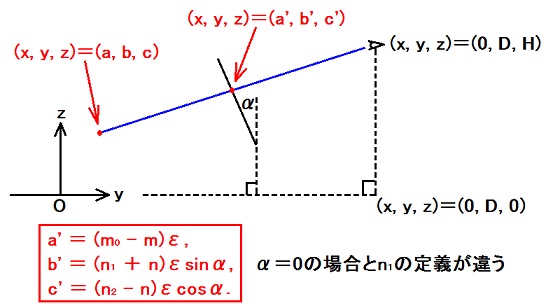
これで、また、
|
y軸が直線m=m0として写っている。 (a, b, c) = (1メートル, 0, 0)ならばm=m1である。 (a, b, c) = (0, 0, 0)ならばn=n20である。 |
不 採 用 |
α > 0の場合の測定方法として考えられる物を以下に列挙する。
(1) カメラの俯角(ふかく)を分度器で直接測定する事によってαの値を知る。
(2) 写真画面の中央に位置する点が光軸に対応しているとして光軸とy軸の交点の座標からαを求める。
(3) xy平面内の三角形とその写真の形の食い違いをもとにαを求める。
(2)では、光軸とy軸の交点の座標を(x, y, z) = (0, β, 0)とすると、H/(D - β) = tanα.
しかし、この方法では、先にxy平面上に筆記具で印を付け、その後で写真画像内のその印の(m, n)を測定する事が出来ない。
また、αが小さい場合には、光軸とy軸の交点が原点から遠く成り過ぎ扱えない。
(3)では、カメラの位置座標と三角形の位置・形・大きさを変えなければ、写真画面の位置に関係なく三角形の写真の形(大きさは違う)はαだけに依存する。
依存性は鋭敏とまでは言えない。
このアイデアを活かすには実際には、y軸上の線分とx軸上の線分の長さの比が被写体と写真でどう違うかを調べるのが良さそうだ。
以下では、(3)の路線で考えてみる。
y軸が直線m = m0として写っている。 (a, b, c) = (β, 0, 0)ならば(m, n) = (MA, NA), (a, b, c) = (-β, 0, 0)ならば(m, n) = (MB, NB), (a, b, c) = (0, β, 0)ならば(m, n) = (MC, NC), (a, b, c) = (0, -β, 0)ならば(m, n) = (MD, ND), --- 測定結果が以下の2つの等式を満たす事は、測定する前から予想される。 MA + MB = 2m0, NA = NB, MC = MD = m0. |
(a', b', c') = (0, D, H) + k(a - 0, b - D, c - H)
∴ (m0 - m)ε = ka and (n1 + n)εsinα = D + k(b - D) and (n2 - n)εcosα = H + k(c - H)
(n1 + n2)εsinαcosα = Dcosα + Hsinα + k[(b - D)cosα + (c - H)sinα]
k = [(n1 + n2)εsinαcosα - Dcosα - Hsinα]/[(b - D)cosα + (c - H)sinα]
m = m0 - ka/ε = m0 - (a/ε)[(n1 + n2)εsinαcosα - Dcosα - Hsinα]/[(b - D)cosα + (c - H)sinα]
n = -n1 + D/(εsinα) + (b - D)[(n1 + n2)εsinαcosα - Dcosα - Hsinα]/{(εsinα)[(b - D)cosα + (c - H)sinα]}
= D/(εsinα) + {(b - D)[(n1 + n2)εsinαcosα - Dcosα - Hsinα] - n1(εsinα)[(b - D)cosα + (c - H)sinα]}/{(εsinα)[(b - D)cosα + (c - H)sinα]}
= D/(εsinα) + [(b - D)(n2εsinαcosα - Dcosα - Hsinα) - n1εsinα(c - H)sinα]/{(εsinα)[(b - D)cosα + (c - H)sinα]}
= D/(εsinα) + {[n2(b - D)cosα - n1(c - H)sinα]εsinα - (b - D)(Dcosα + Hsinα)}/{(εsinα)[(b - D)cosα + (c - H)sinα]}
= {[n2(b - D)cosα - n1(c - H)sinα]εsinα - (b - D)(Dcosα + Hsinα) + D[(b - D)cosα + (c - H)sinα]}/{(εsinα)[(b - D)cosα + (c - H)sinα]}
= {[n2(b - D)cosα - n1(c - H)sinα]εsinα - b(Dcosα + Hsinα) + D(bcosα + csinα)}/{(εsinα)[(b - D)cosα + (c - H)sinα]}
= {[n2(b - D)cosα - n1(c - H)sinα]εsinα + (cD - bH)sinα}/{(εsinα)[(b - D)cosα + (c - H)sinα]}
= [n2(b - D)cosα - n1(c - H)sinα + (cD - bH)/ε]/[(b - D)cosα + (c - H)sinα].
まだ正式な検算はしていませんが、式の各所に対称な特徴が貫かれている(y座標に関する因子とz座標に関する因子が互い違いに入っている)ので、多分これで合ってると思う。
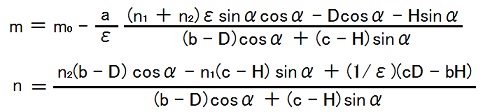
この式を使うと、
MA = m0 + (β/ε)[(n1 + n2)εsinαcosα - Dcosα - Hsinα]/(Dcosα + Hsinα),
MB = m0 - (β/ε)[(n1 + n2)εsinαcosα - Dcosα - Hsinα]/(Dcosα + Hsinα),
∴ MA + MB =2m0 and MA - MB = 2(β/ε)[(n1 + n2)εsinαcosα - Dcosα - Hsinα]/(Dcosα + Hsinα).
NA = NB = (n2Dcosα + n1Hsinα)/(Dcosα + Hsinα).
MC = MD = m0.
NC - ND = [n2(β-D)cosα + n1Hsinα - (1/ε)βH]/[(β - D)cosα - Hsinα]
- [n2(-β - D)cosα + n1Hsinα + (1/ε)βH]/[(-β - D)cosα - Hsinα]
= [n2(β-D)cosα + n1Hsinα - (1/ε)βH]/[(β - D)cosα - Hsinα]
- [n2(β + D)cosα - n1Hsinα - (1/ε)βH]/[(β + D)cosα + Hsinα]
= {[n2(β-D)cosα + n1Hsinα - (1/ε)βH][(β + D)cosα + Hsinα] - [n2(β + D)cosα - n1Hsinα - (1/ε)βH][(β - D)cosα - Hsinα]}/{[(β - D)cosα - Hsinα][(β + D)cosα + Hsinα]}
これらから(NC - ND)/(MA - NB)を求めれば、αを特定できるのではないか、と考えたが。
(m0 - m)ε = a[(n1 + n2)εsinαcosα - Dcosα - Hsinα]/[(b - D)cosα + (c - H)sinα],
(n1 + n)εsinα - D = -D + ε(sinα)[(n1 + n2)(b - D)cosα + (1/ε)(cD - bH)]/[(b - D)cosα + (c - H)sinα]
= {[ε(n1 + n2)sinα - D](b - D)cosα + (D - b)Hsinα]/[(b - D)cosα + (c - H)sinα]
= (D - b){Hsinα - [ε(n1 + n2)sinα - D]cosα]/[(b - D)cosα + (c - H)sinα],
,
(n2 - n)εcosα - H = -H + ε(cosα)[(n1 + n2)(c - H)sinα - (1/ε)(cD - bH)]/[(b - D)cosα + (c - H)sinα]
= {[ε(n1 + n2)cosα - H](c - H)sinα + (H - c)Dcosα}/[(b - D)cosα + (c - H)sinα]
= (H - c){Dcosα - [ε(n1 + n2)cosα - H]sinα}/[(b - D)cosα + (c - H)sinα]
直線の方向ベクトルは、
(a[(n1 + n2)εsinαcosα - Dcosα - Hsinα],
(b - D){[(n1 + n2)εsinα - D]cosα - Hsinα],
(c - H){[(n1 + n2)εcosα - H]sinα - Dcosα})
これは、(a, b - D, c - H)に平行。
自明な結論を出してしまった。
mとnを代入したのがいけなかったようだ。私でもこんな風に間違えますからね。
直線の方向のベクトルは、
((m0 - m)ε, (n1 + n)εsinα - D, (n2 - n)εcosα - H)
このベクトルを、ε, n1, n2, αを使わずに表せ、という問題を解かなくちゃいけない。
α = 0の場合は、m1, n1という2つの測定値を使って、n0, ε, dという3つの未知値変数を消去しました。
α > 0の場合は、未知値変数は、m0, n1, n2, ε, αの5つです。
このうちのm0は、α=0の場合と同様に直接測定可能ですが、ここでは直接測定しない方法を考えます。
α > 0の場合は測定値として、MA, MB, NA=NB, NC, NDの5つを使ってみます。
これで、消去したい未知値変数と測定値の個数は同じだから、α=0の場合と同様に消去できそうだ、と見込めます。
まず、MA + MB = 2m0 ∴ m0 = (1/2)(MA + MB).
したがって、ここから先はm0を既知定数と考えて、MA - MB, NA = NB, NC, NDという4つの測定値を使って、n1, n2, ε, αという4つの未知値変数を消去する事を考えます。
α=0の場合を参考にすると、n1とn2を消去する過程でεも消えてしまう事が期待されます。
やってみましょう。
D(MA - MB) - 2β(sinα)NA
= [2βD(sinα)(cosα)n1 + 2β(sinα)(Dcosα - Hsinα)n1 - 2(βD/ε)(Dcosα + Hsinα)]/(Dcosα + Hsinα)
= 2β(sinα)(2Dcosα - Hsinα)n1/(Dcosα + Hsinα) - 2βD/ε
∴ n1 = [D(MA - MB) - 2β(sinα)NA + 2βD/ε](Dcosα + Hsinα)/[2β(sinα)(2Dcosα - Hsinα)].
H(MA - MB) - 2β(cosα)NA
= [2βH(sinα)(cosα)n2 - 2β(cosα)(Dcosα - Hsinα)n2 - 2(βH/ε)(Dcosα + Hsinα)]/(Dcosα + Hsinα)
= - 2β(cosα)(Dcosα - 2Hsinα)n2/(Dcosα + Hsinα) - 2βH/ε
∴ n2 = [H(MA - MB) - 2β(cosα)NA + 2βH/ε](Dcosα + Hsinα)/[2β(cosα)(2Hsinα - Dcosα)].
(n1 + n)εsinα - Dからεをくくり出せるか、手応えを見るために、n1εsinα - Dを計算してみます。
n1εsinα - D
= [D(MA - MB)εsinα - 2βε(sinα)2NA + 2βDsinα](Dcosα + Hsinα)/[2β(sinα)(2Dcosα - Hsinα)] - D.
分子だけ計算すると、
[D(MA - MB)εsinα - 2βε(sinα)2NA + 2βDsinα](Dcosα + Hsinα) - 2βD(sinα)(2Dcosα - Hsinα)
= [D(MA - MB)εsinα - 2βε(sinα)2NA](Dcosα + Hsinα) + 2βD(sinα)(2Hsinα- Dcosα)
行き詰った。
計算ミスを探します。
2024年12月03日夜、食事や休憩をしている時にやり方が分かった。
「宇田君、そんな事しなくたってさあ」と言われる前に言っておこう。
z'軸がスクリーンに平行、y'軸がスクリーンに垂直な座標系x'y'z'を使えば、α=0の場合の結論を利用できる。
そうやって直線の方程式を(x', y', z')で表しておき、それを座標変換で(x, y, z)についての方程式に書き換えればよい。
αの値以外はこれで必ず求まるので、2024年12月03日昼にやった計算も、計算ミスを直せば同じ結果に至る事でしょう。
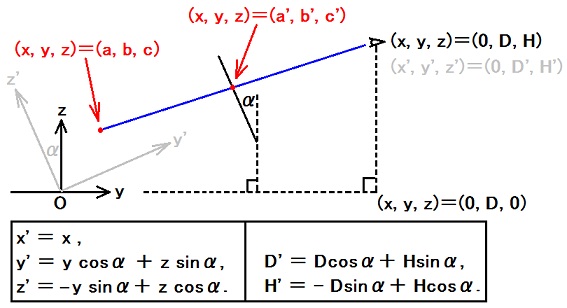
直線の方程式は、1メートルの代わりにβを使うと、
(x', y', z') = (0, D', H') + k(β(m0 - m), -D'(m0 - m1), -H'(m0 - m1) + β(n1 - n)).
この式を
(x, y, z) = (x', y'cosα - z'sinα, y'sinα + z'cosα)
に代入すると、
(x, y, z) = (0, D, H) + k(β(m0 - m), (H'sinα - D'cosα)(m0 - m1) - β(n1 - n)sinα, -(D'sinα + H'cosα)(m0 - m1) + β(n1 - n)cosα)
⇔ (x, y, z) = (0, D, H) + k(β(m0 - m), -D(m0 - m1) - β(n1 - n)sinα, -H(m0 - m1) + β(n1 - n)cosα).
ただし、n1の定義としては、α=0の場合の定義を使っています。
残るはαの値の測定だけです。
NCの値を使おうと思う。
(a, b, c) = (0, β, 0)である点の(x', y', z')座標は、
(x', y', z') = (0, βcosα, -βsinα)
NCは以下の式で決まる。
(n0 - NC)ε = c' = H' + (-βsinα - H')(D' - d)/(D' - βcosα)
∴ (n0 - NC)ε = -Dsinα + Hcosα + (-βsinα + Dsinα - Hcosα)(Dcosα + Hsinα - d)/(Dcosα + Hsinα - βcosα)
∴ (n0 - NC)ε = [- Hβ + d(β - D)sinα + Hdcosα]/[(D - β)cosα + Hsinα]
n1の式も使ってみる。
(n0 - n1)ε = c' = H' + (0 - H')(D' - d)/(D' - 0)
∴ (n0 - n1)ε = H' - H'(D' - d)/D' = H'd/D' = (-Dsinα + Hcosα)d/(Dcosα + Hsinα)
行き詰った。
[(n0 - n1)ε - (n0 - NC)ε]÷[(m0 - m1)ε]を計算して、途中でdが消えて結果がD, H, αだけの式に成る事を見込む、それで出来なければ諦める、という心境に2024年12月04日夜至った。
んじゃ、清書に行きます。
スポーツの試合のビデオ判定に応用する場合は、まず複数台のビデオ・カメラの時計を正確に揃え、その後で、それら複数台のビデオ・カメラで、同一の被写体を異なる方向から撮影します。
時計合わせをせずに、事前または事後に同一のストップ・ウォッチの表示を数秒間だけビデオ撮影して、その結果を使ってビデオ・カメラの時計のズレを知る、という方法でもよい。
選手の身体が邪魔に成って必要な位置がカメラから見えない場合に備えて、y軸の正の部分の真上、y軸の負の部分の真上、x軸の正の部分の真上、x軸の負の部分の真上、以上4箇所に合計4台のビデオ・カメラを設置して、それらの時計を正確に揃えます。
大きな大会では、原点の真上から見下ろす第5のビデオ・カメラも使った方が良かろう。
異なるビデオ・カメラの向きの違いは本当は90度よりも小さい方が死角が生じ難いかもしれない。
しかし、そうすると計算がもう少し面倒に成る。