
since 2003
イレコナビ サイトマップ
ケンパ・ステップは、BFSで踏み切り着地時にAFS基本構えを作る運足です。
凝縮するための具体的な技術として私が考案しました。
ケンケンパッパ、ケンパッパ、ケンパッ、ケンパッ、ケンパッパという掛け声とともに片足立ちに成ったり両足立ちに成ったりを繰り返しながら前進する子供の遊びが有るが、命名は、これに基づく。
BFS基本構えとAFS基本構えの関係から、BFSのハーフステップを角θだけ前足の方へズラして跳び、着地して直ぐに足を踏み変えず向きだけ変えてAFS基本構えに移行した時に、敵の重心が自分の重心の真正面に有る為には、θと跳び幅Lは下図の関係になければいけない。
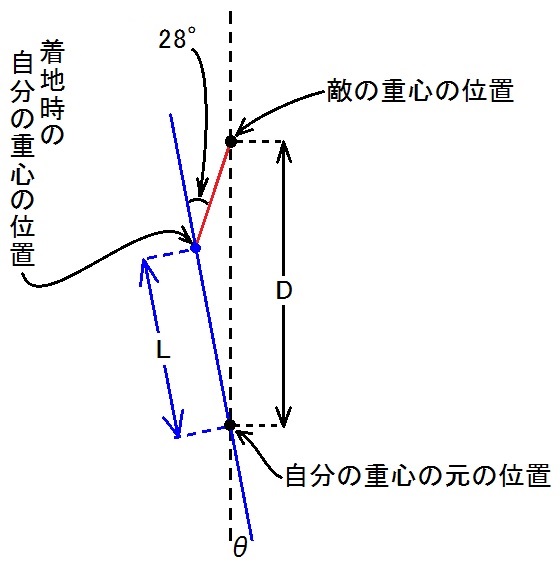
敵の重心から青線に下ろした垂線の長さを2通りに表す事によって、Lとθの関係を求める事が出来る。
D sinθ = (D cosθ- L)tan28°
∴ L = D cosθ - D sinθ/tan28°
∴ L = D(cosθ - sinθ/tan28°)
着地時の重心間距離は
(D cosθ - L)/cos28°
= (D sinθ/tan28°)/cos28°
= D sinθ/sin28°
着地時の重心間距離=1ウデ、L=1ウデの場合には、2等辺三角形に着目してθ=14°だと分かります。
この場合、D = 2 × cos14°× 1ウデ ≒ 2 × 0.9703 × 1ウデ ≒ 1.94ウデ
これは、真半身で前足の爪先が触れ合っている場合の重心間距離0.92スネ×2=1.84スネ=1.51ウデよりも大きいので、このステップで凝縮を実現する事は可能だと判断できる。
D=1.51ウデの場合に、着地時の重心間距離=1ウデとするためには、
1ウデ = 1.51ウデ × sinθ/sin28°
∴ sinθ=(1/1.51)sin28°=(1/1.51)×0.4695 = 0.311
∴ θ≒18°
L = 1.51ウデ × (cos18°- sin18°/tan28°)
= 1.51ウデ × (0.951- 0.311/0.5317)
≒ 0.55ウデ
という風にハーフステップに余裕が残る。
相手も自分も真半身に構えて前腕を前方に突き出し、掌底を接している状態では、重心間距離は2.18ウデぐらいらしい、という事が、自分の体で測ってみて分かった。
これはBFS空手の試合での膠着状態の典型的な重心間距離だが、上記データは、これには足りないかもしれない。
ケンパ運足を実際にやってみると、なぜか、θ=0で跳んで、着地後に向きを直すのではなく着地時にはAFS構えに成っている様に出来る。
それで、着地時のAFS構えにとって敵の重心は自分の重心の真ん前に有る。
これは、空中で、足の配置を変えるのと上体の向きを半身にひねるのが角運動量的に打ち消し合うためではないか。
やってみた実感としては、足を開こうとは全く考えず、体を半身に開くつもりでやると、ちゃんと成っていた。
前方への跳び幅には、普通のハーフステップとの違いは見られなかった。