
since 2003
イレコナビ サイトマップ
先後相補BFS対は、自分が先手を打ってBFSを行なう事と、バックステップ後先BFSの、相補性を用いて、片方でけん制してもう片方で捕る戦術です。
相手のバランスがどちらかに崩れれば、原理的には捕れるはずです。
バックステップ後先BFSを成功させるためには、Dを出来るだけ大きくする必要が有るのだったが、Dを大きくするためには、入って来たらこっちが先に撃つぞ、という風に先攻BFSでけん制するのが有効だ。
けん制はただの脅しではなく、実際に、Dが小さく成り過ぎたら、直ぐにこちらが先攻する。
こうして、先攻と反応攻の相補対が出来る。
先BFSとバックステップ後先BFSの相補化は、次の被覆シートで定式化できる。
| 敵の様子 | 自分の反応 | 注釈 | |
| 領域(1)でBFSを開始した。 | バックステップ無しBFSで敵のBFSの終点を攻める。 | 敵のBFSは届かない。 | いずれの場合にも自分は、敵の運足が準備移動なのかBFSジャンプなのかを見切らなくてはいけない。 また、Dが(1)(2)(3)のうちのどれに入っているかを目測できなくてはいけない。 |
| 攻撃準備として(1)から(2)へ移動した。 | 様子を見る。 | 自分のBFSは敵に届くが、これを敵はバックステップで交わす事が出来る。 | |
| 攻撃準備として(2)から(3)へ移動した。 | 敵がBFSを開始する前に、BFSを開始する。 | 敵のDBも自分のと同じならば、敵がこちらのBFSをバックステップで交わす為には、D + DB > DRでなければいけないが、D < DC and DR = DC + DBだから、これは無理だ。 | |
| (3)へ移動せず(2)でBFSを開始した。 | DBだけバックステップ後先BFSで敵のBFSの終点を攻める。 | 敵のDRも自分のと同じならば、敵のBFSが有効である為にはDR > DC + DBでなくてはいけないが、実際はDR = DC + DBだ。 | |
まず、変数Dと定数DRと定数DCを、次の様に定義する。
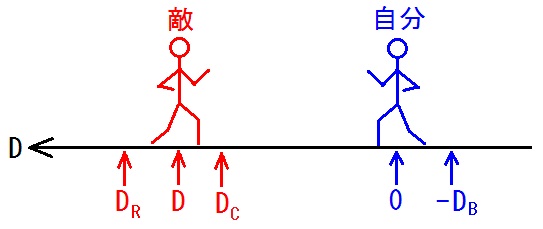
自分の重心の位置はD軸の原点の上です。
自分は、ここで待機します。
敵の位置を変数Dで表します。
DRはダイナミックリーチであり、定数です。
D軸の原点の真上から発射した自分のBFSが有効と成るDの最大値がDRです。
DBは、攻撃準備状態を保ったまま態勢を崩さず行なえるバックステップの重心移動距離の最大値です。
DBは定数です。
DCは、最大限バックステップした位置から発射した自分のBFSが有効と成るDの最大値です。
DC ≡ DR - DB
DCは定数です。
DCをcritical distance(臨界距離)と呼ぶ事にする。
こうして定義されたD, DR, DCを使って、領域(1)(2)(3)は、以下の不等式で定義される。
(1) D > DR
(2) DR > D > DC
(3) DC > D
---
さて、以上は、私が頭の中で考えた事です。
したがって、実際にやってみると、色々と上手く行かない所が見付かると思います。
そもそも、バックステップ後先BFSという物が、後方で一旦速度ゼロに成る為に、バックステップからBFSへの切り返しが、どうしても緩慢に成り、時間的に間に合わなく成る、という問題を抱えている様に感じます。
BFS先制攻撃のけん制効果でDを出来るだけ大きくさせる事によって、この問題が解決されるかが、見所だと思う。
具体的な数値を割り出す事も、課題として残される。