
since 2003
イレコナビ サイトマップ
2015年02月07日の記事の計算を、今日は近似無しでやってみる。
ただし、重心を上下させない、という条件は、今まで通り使う事にする。
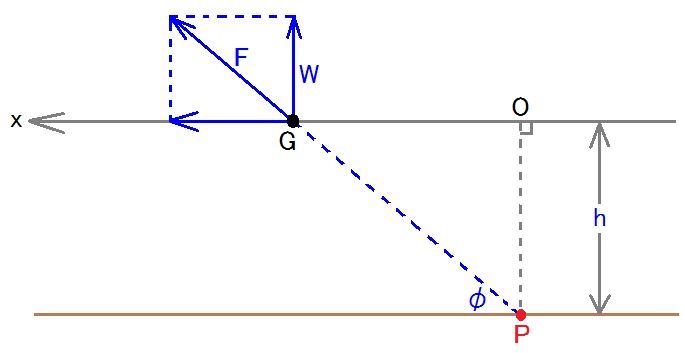
Fsinφ=W
∴F=W/sinφ
x tanφ=h
∴x=h/tanφ
∴dx=h(-1-1/tan2φ)dφ=(-h/sin2φ)dφ
重心がされる仕事を計算するための不定積分は、
∫dx Fcosφ
=∫dφ(-h/sin2φ)(W/sinφ)cosφ
=-hW∫dφcosφ/sin3φ
=(hW/2)(1/sin2φ)
=(hW/2)(1+1/tan2φ)
=(hW/2)[1+(x/h)2]
だから、x=x0からx=x1まで加速されるとすると、その間に重心がされる仕事は、
(hW/2)[1 + (x1/h)2] - (hW/2)[1 + (x0/h)2]
= (hW/2)[(x1/h)2 - (x0/h)2]
これが加速終了時の重心の運動エネルギーに等しいから、
(1/2)(W/g)(加速終了時の重心の速さ)2=(hW/2)[(x1/h)2 - (x0/h)2]
∴(加速終了時の重心の速さ)=√{gh[(x1/h)2 - (x0/h)2]}
身体のGP間の部分の伸び切った瞬間の長さをLGPとすると、
x2 + h2 ≦ LGP2。
∴(x/h)2 ≦ (LGP/h)2 - 1
だから、x0とx1の範囲は、
(x0/h)2 < (x1/h)2 ≦ (LGP/h)2 - 1
で定まる事が分かる。
特に、
x0 = 0
(x1/h)2 = (LGP/h)2 - 1
の場合には、
(加速終了時の重心の速さ)=√{gh[(LGP/h)2 - 1]}
ここまで近似無しだ。
LGPとして爪先立ち(前底足で閉脚直立)の時のヘソの高さを用いると、私の場合これは測ってみると約114cmだった。
hとして、腰をPの真上に配置し膝を直角に曲げた時のヘソの高さを用いると、私の場合これは測ってみると約82cmだった。
これらの数値を使って計算すると、
(加速終了時の重心の速さ)≒√{9.8m/s2×0.82m×[(114/82)2 - 1]}≒2.74m/s
07日@2015年02月@日記の近似式を使った計算結果(2.6m/s)が、ハーフステップ@デザイン例@理論@武道に書かれているが、それよりは大きい値が算出できて嬉しい。
幾ら鍛えても、これ以上には成らない様だ。
一連の考察を通じて、結局ハーフステップBFSは水平方向への自由落下だ、という事が良く分かった。