
since 2003
イレコナビ サイトマップ
足首から先を省略し、股関節と重心の違いも無視する近似を採用する。
また、脚の膝から上の長さと膝から下の長さは両方ともLだ、という風に近似する。
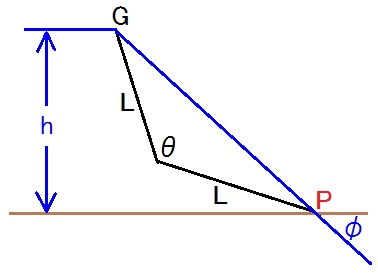
すると、図より
2L sin(θ/2) sinφ=h
一方、昨日の記事に書かれている事から、
F(θ)sinφ=W
ここまでを組み合わせると、
2L sin(θ/2) W/F(θ)=h
∴F(θ)=(2L/h)W sin(θ/2)
この関数のグラフと、脚力の最大値のグラフを、以下に重ねて描く。
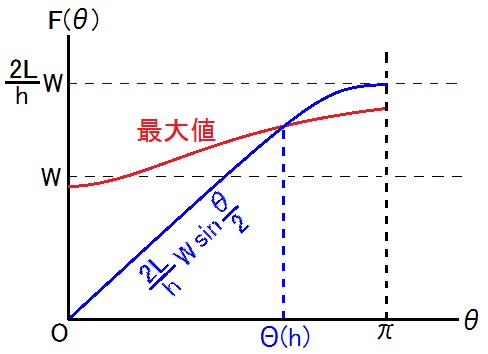
人によっては F(0)の最大値≧W な人も居る。
グラフの交点のθ座標をΘ(h)とする。
交点が存在しない場合は便宜上、
Θ(h) > π
と考える事にする。
d[2L sin(θ/2)]=L cos(θ/2) dθ
脚が重心にする仕事は
∫ab F(θ)L cos(θ/2) dθ
= (2L2/h)W∫ab dθsin(θ/2)cos(θ/2)
= (L2/h)W∫ab dθsinθ
= (L2/h)W[cos(a) - cos(b)]
ただし、
a ≧ (φ=π/2の時のθの値) = 2 sin-1[h/(2L)]
b = [Θ(h)とπのうちの小さい方]
脚が重心にした仕事が加速終了時の重心の運動エネルギーに等しいから、
(1/2)(W/g)(加速終了時の重心の速さ)2 = (L2/h)W[cos(a) - cos(b)]
∴(加速終了時の重心の速さ) = √{2(L2/h)g[cos(a) - cos(b)]} = √{(2L/h)[L cos(a) - L cos(b)]g}