
since 2003
イレコナビ サイトマップ
日本物理学会2011年春季(第66回年次)大会は、東北地方太平洋沖地震の影響で中止と成りましたが、中止決定より前に既に講演概要集が発行されているので、発表は成立したものと見なされるそうです。 →中止に関する会長メッセージ
また、資料公開サイト(口頭で発表する代わりにウェブで発表するという形式を取るための手段)が設置されています。→第66回年次大会講演資料公開サイトについて
私の発表は、25aGC-1「新文法版量子論の確率解釈」と28aEB-11「クレプシュゴルダン係数の解説の盲点」の2つです。
| 2011年03月11日 | 東北地方太平洋沖地震発生。 |
| 2011年03月15日 | 日本物理学会第66回年次大会中止通知メール受信。 |
| 2011年03月17日 | 「本年次大会での発表について、口頭発表およびポスター発表において質疑はできませんでしたが、すでに概要集を発行しておりますことから、本年次大会での発表は成立したものといたします」 という文と 「年次大会開催に代わり、発表資料あるいはそれに相当するものの掲載をWeb上で公開することを検討いたします」 という文を含むメールを受信。 |
| 2011年03月25日 | 25aGC-1「新文法版量子論の確率解釈」発表予定日。 この発表は地震のため中止された。 |
| 2011年03月28日 | 28aEB-11「クレプシュゴルダン係数の解説の盲点」発表予定日。 この発表は地震のため中止された。 |
| 2011年03月30日 | 第66回年次大会講演資料公開サイト設置が決定された事を通知するメールを受信。 このメールに「このサイトに資料が掲載された一般講演についてのみ発表が成立したことといたします」と書かれていた。 |
| 2011年04月01日 | 25aGC-1「新文法版量子論の確率解釈」の講演資料(※)を学会のサーバーにアップロード開始。 |
| 2011年04月25日 | 25aGC-1「新文法版量子論の確率解釈」の講演資料(※)を学会のサーバーにアップロード完了。 |
| 2011年05月06日 | 講演資料公開サイト開始。 25aGC-1と28aEB-11の発表成立。 28aEB-11については講演概要が表示されます。 |
| 2011年05月07日 | 自宅のパソコンから講演資料公開サイトにアクセスし、25aGC-1の資料(※)と28aEB-11の講演概要が表示される事を確認した。 |
| 2011年08月11日 | 誤ってhttp://w2.gakkai-web.net/gakkai/jps/pdf/を閲覧し、講演資料公開サイトで公開されている25aGC-1の講演資料(※)が無断で概要集原稿に差し替えられている、と早合点した。 講演資料公開サイト(2011年05月06日に受信したメールにアドレスが記載されている)を閲覧すると、25aGC-1の講演資料(※)が正しく表示された。 |
| 2011年08月31日 | 15時17分に25aGC-1の講演資料(※)が正しく表示される事を講演資料公開サイトで確認した。 講演資料公開サイト終了。 |
| 講演概要 |  25aGC-1 |
日本物理学会講演概要集 第66巻 第1号 第1分冊 2ページ。 |
|
 28aEB-11 |
日本物理学会講演概要集 第66巻 第1号 第2分冊 444ページ。 |
||
※25aGC-1「新文法版量子論の確率解釈」の講演資料は、以下に掲載されている背景白色の部分をPDFに変換したものです。
5
a
G
C
-
1
∧
新
文
法
版
量
子
論
の
確
率
解
釈
∨
の
講
演
資
料
| 25aGC-1 | 新文法版量子論の確率解釈 | ||||
| www.GrammaticalPhysics.ac 宇田雄一 | |||||
| このPDFファイルをダウンロードして自分のパソコンのハードディスクに保存して頂けると幸いです。これは義務ではありません。 | |||||
| §A | 量子力学では、時刻tに(x,y,z)を測定したとき、 測定結果が(x,y,z)∈Ωを満たす確率は、 規格化された波動関数ψを使って、 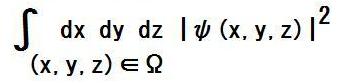 で与えられる、とされる。 これに倣って、新文法版量子力学では、 全ての時刻に(x,y,z)を測定した場合、 測定結果がχ∈Χを満たす確率は、 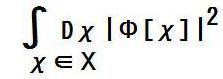 で与えられる、と仮定してみたい。 ただし、χは、 χ(t)=[時刻tにおける(x,y,z)] である様な関数だとし、Χは関数を元に持つ集合だとする。 規格化の問題は保留とする。 |
||||
| §B | さらに、 t∈Tなる全ての時刻tに(x,y,z)を測定し、 not(t∈T)なるどの時刻tにも全く測定を行わなかった場合、 測定結果が ∀t∈T; χ(t)∈Χ(t) を満たす確率は、 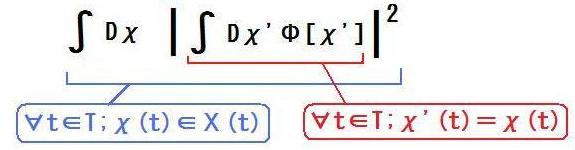 で与えられる、と仮定してみたい。 この式は、 T内のχ'(t)をχ(t)に固定してΦ[χ']をTの外の全てのχ'(t)について多重積分した後で絶対値二乗を取ったものが、測定結果がχに成る確率密度だ、 という意味だ。 ここでのΧは§AのΧとは別物です。 絶対値二乗を取る前にχ'で積分している点に注目してください。 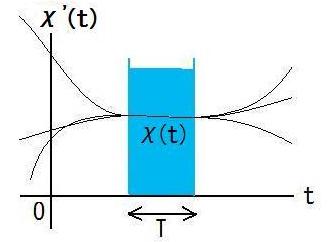 |
||||
| §C | この事は、量子力学で言うと(新文法版の量子歴史を旧文法版の量子状態に喩えて言うと)、 時刻tに、xとzを測定し、yを全く測定しなかった場合に、測定結果が(x,z)∈ωを満たす確率を 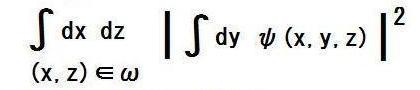 だと仮定する事に相当する。(ωは2次元領域) この式は、x,zを固定して波動関数をyで積分した後で絶対値二乗を取ると、測定結果が(x,z)に成る確率密度が得られる、という意味です。 絶対値二乗を取る前にyで積分している点に注目してください。 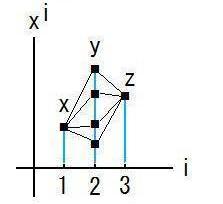 旧文法版のこの仮説を実験で検証する事によって、新文法版の仮説に見込みがあるか否かを占う事ができるので、 ぜひ実験物理学者に、この仮説の検証をお勧めしたい。 もし実験結果によって私の予想が反証されても、測定されていない時のyの値が確定しているのか否か、の検証実験と成ります。 新文法版と旧文法版を合わせて、一言で言うと、これは、 確率を求めるには、波動関数を、測定しなかった変数について先に足して、その後で絶対値二乗を取れ、 という事であり、二重スリット実験から得られた教訓の普遍化と言える。 この処方は、当たっていれば、パウリの排他原理と並ぶものとして、量子論の基本原理に付加されるだろう。 |
||||
| §D | 新文法の話に戻ります。 特に、Tが2つの時刻t1,t2のみから成る場合、つまり、T={t1,t2}の場合、§Bの式の絶対値記号の中身は、 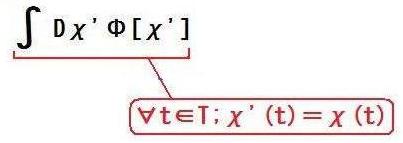 これは、t=t1とt=t2でのχ'(t)の値を固定してΦ[χ']を他の全ての時刻のχ'(t)について多重積分したもの、です。 これがファインマン経路積分の正体なのではないか? 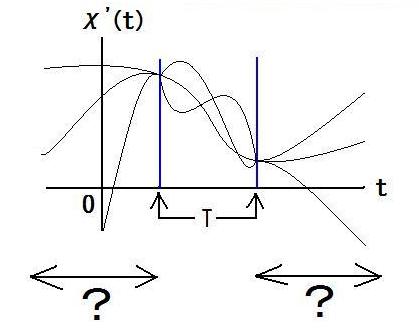 ただし、ファインマン経路積分には、この図の?部分がありませんが。 |
||||
| §E | §Aから§Dまでの考え方にはいくつか気になる点があるので、以下にそれを列挙しておきます。 | ||||
| 1 | 問題 | 問題 | エーレンフェスト定理では積分する前に絶対値二乗を取っている。 | ||
| 説明 | エーレンフェスト定理は測定が行なわれない場合の話と考えられ、絶対値二乗を取った後で測定されない自由度について積分している。 | ||||
| 所見 | やはり、絶対値二乗を取る前に積分したのでは駄目なのかもしれない。 | ||||
| 2 | 問題 | 問題 | 絶対値二乗を取る前に積分すると規格化の保存が出ない。 | ||
| 説明 | 旧シュレディンガー方程式から(d/dt)∫dx∫dz|∫dyψ(x,y,z;t)|2=0を導く事は出来ない。 | ||||
| 所見 | 規格化の保存は、論理的に絶対に必要な事、ではないので、出なければ出ないでも良いのではないか。 | ||||
| 3 | 問題 | ファインマン経路積分(作用汎関数の経路積分)ではt1以前とt2以後の時間領域で積分しないが、この点が量子歴史Φの経路積分と違う。 | |||
| 所見 | 所見 | t<t1とt2<tでの積分からは定数因子が出るならば、この違いは本質的ではないが、そう成るだろうか? 自由粒子の伝播関数を使って、円環時間でT→∞とした場合を考えれば、感触をつかめそう。 |
|||
| 補足 | 円環時間の使用については日本物理学会2009年秋季大会13pSH-3(http://15.pro.tok2.com/~wooder/PhysSoc/09au/)で発表した。 | ||||
| 4 | 問題 | 問題 | t1≦t≦t2の外での測定がt1,t2での測定結果の関係に影響を及ぼしてしまって良いのか? | ||
| 説明 | t1<t2<t3なる3時刻で測定を行なった場合、因果律の観点からt3での測定の有無はt1,t2での測定結果に影響を及ぼすはずがないので、測定結果の確率分布P(χ(t1),χ(t2),χ(t3))をχ(t3)で積分すれば、t3で測定を行なわなかった場合の確率分布P(χ(t1),χ(t2))が得られるはずだが、P(χ(t1),χ(t2))の計算においては絶対値二乗を取る前にχ(t3)で積分しているので、そう成らないだろう。 | ||||
| 所見 | 所見 | 量子歴史として作用汎関数を考える場合等の特殊な場合には上記の不都合が起こらない、かも知れない。 一般の場合には上記の不都合が起こるのが現実であり、その事によって因果律は否定されるのかもしれない。 あるいは、量子歴史に境界条件の様なものを課す事によって、因果性を保守する事が可能なのかもしれない。 |
|||
| 補足 | 量子歴史として作用汎関数を考える事については、日本物理学会2010年春季大会20pBJ-1(http://15.pro.tok2.com/~wooder/PhysSoc/10sp/)で発表した。 | ||||
| 5 | 問題 | 問題 | 旧シュレディンガー方程式の解の無限乗積で表される量子歴史の解釈が、前時刻での測定が後時刻での測定に影響を及ぼすという事実に反し、それの経路積分の結果が作用汎関数の経路積分の結果に一致し得ない。 | ||
| 説明 | 旧シュレディンガー方程式の解の無限乗積で表される量子歴史は、各因子が同一の解の異なる時刻での値、つまり、測定が行なわれなかった場合の波動関数の無限乗積、であったのに対して、作用汎関数の経路積分の結果は、前時刻で測定が行なわれた場合の後時刻での波動関数だから、両者は明らかに異なる。 旧方程式の解の無限乗積で表される量子歴史については、日本物理学会2006年春季大会27pXA-6(http://15.pro.tok2.com/~wooder/PhysSoc/06sp/)で発表した。 |
||||
| 所見 | 所見 | 旧方程式の解の無限乗積は新方程式の解に成らず、新方程式の解は必ず時間方向にエンタングルしており、そのため異時刻の測定結果が相関するのだろう。→※ | |||
| 補足 | 新文法版シュレディンガー方程式を作るときには、量子歴史を旧波動関数の無限乗積と考える発想を使ったが、あれから随分と時間が経って、今の私はそれと矛盾する事を言う様に成っている。 時間方向にエンタングルしてない場合が旧量子力学だ、という当初の主張を訂正して、時間方向のエンタングルによって旧量子力学の観測問題への解答が出て来る、という主張も候補として提起したい。 この事は、波束の収縮の問題に対して、そもそも波束の収縮という現象自体が存在しない、という答え方を提案するものである。 また、他の解(旧量子力学で表現できない本質的に新しい解)もあるかもしれない。 新文法版シュレディンガー方程式については、日本物理学会2007年春季大会28pSL-11(http://15.pro.tok2.com/~wooder/PhysSoc/07sp/)で発表した。 しかし時間方向にエンタングルしていない解も見付けた。(http://15.pro.tok2.com/~wooder/GramPhys/html/modules/news/article.php?storyid=84) |
||||
| 6 | 問題 | 問題 | 作用汎関数を量子歴史とすると、エーレンフェスト定理が出ない。 | ||
| 説明 | 作用汎関数は新文法版シュレディンガー方程式の解に成っていないので、新文法版シュレディンガー方程式から導出されるエーレンフェスト定理に従わない。 作用汎関数は時間並進不変だから、位置の期待値の加速度が常にゼロに成ってしまう。 エーレンフェスト定理については、日本物理学会2008年春季大会25pZC-1(http://15.pro.tok2.com/~wooder/PhysSoc/08sp/)および日本物理学会2008年秋季大会23pSP-10(http://15.pro.tok2.com/~wooder/PhysSoc/08au/)で発表した。 |
||||
| 所見 | 作用汎関数がエーレンフェスト定理を導出できる他の方程式の解に成っている可能性も考えるべきだ。 エーレンフェスト定理を出せる1つの解を時間方向にズラして全て重ね合わせれば、時間並進不変に成るが、それは依然として新文法版シュレディンガー方程式の解なので、作用汎関数には一致しない。→※ |
||||
| 7 | 問題 | 旧シュレディンガー方程式の全ての解の含蓄は1つの作用汎関数に含まれているから、量子歴史は1つだけではないのか? それなのに、新文法版シュレディンガー方程式には無数の解がある。 |
|||
| 所見 | 作用汎関数は2時刻の測定結果の関係のみに関与し、量子歴史には、それに加えて例えば1時刻のみでの測定結果がどう成るか、という任意性もあるので、量子歴史が無数に成る余地がある。 しかし、量子力学の含蓄は2時刻の測定結果の関係で全てである、という可能性を先験的に否定するのも間違いだろうから、私の予想している方向性で上手く行かない場合には、そちらの可能性も考えてみる必要がある。 |
||||
| ※ | 旧シュレディンガー方程式の1時刻で1点に局在する解の無限乗積で表される量子歴史を時間方向にズラして全て重ね合わせたものは、時間方向にエンタングルしているだろうし、時間並進不変だから、新文法版シュレディンガー方程式の解か作用汎関数に成っている可能性がある。 しかし、作用汎関数は新文法版シュレディンガー方程式の解ではないので、両方に成っている、という事は有り得ない。 新文法版シュレディンガー方程式を改良する事によって、この難点を解消すべきか?できないか? 以下に、厳密でない漫画的な見通しをスケッチしておく。 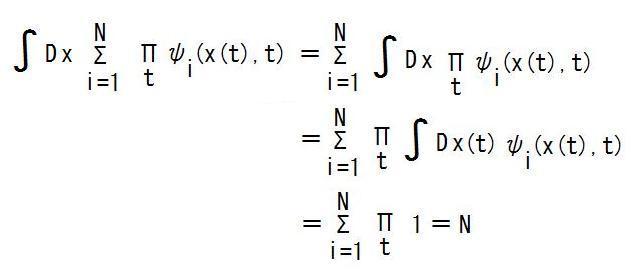 x(t1)とx(t2)をx(t1)=a,x(t2)=bに固定して積分すると、 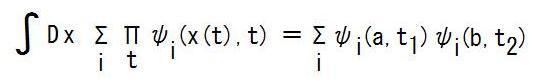 ここで、iはどの時刻にどの位置に局在するかを指定する指標だから、 i=(x,t)と置いて、Σiを∫dx∫dtに書き換えると、この式は、 ∫dx∫dt ψ(x,t)(a,t1)ψ(x,t)(b,t2) と成る。 ψ(x,t)はψ(x,t)(x',t)=δ(x'-x)である様な、旧シュレディンガー方程式の解だ。 これを使って、 ∫dx∫dt ψ(x,t)(a,t1)ψ(x,t)(b,t2)=ψ(a,t1)(b,t2)+ψ(b,t2)(a,t1) と出来れば、ほぼ作用汎関数の経路積分と同じ結果を導出できた事に成りそうだが、怪しい。 |
||||
---
日本物理学会第66回年次(2011年春季)大会講演資料
初回提出日=2011年04月01日
最終上書提出日=2011年04月25日
提出者=宇田雄一