
since 2003
イレコナビ サイトマップ
日本物理学会2010年秋季大会での私の発表は、文法物理学についての12aSC-9「円環時間を用いた新文法版シュレディンガー方程式の求解(2)」と物理教育についての26aQK-10「ゆとり教育導入以前からあった高大接続の不連続性」の2件だった。
講演概要とOHPの内容はこのページの下の方に掲載されています。
同じ様な事を繰り返せば、段々と要領が良く成るもので、今回は、両方とも、行きは新幹線、帰りは普通列車、宿泊なしで、経費節減の極みに至った。
12aSC-9は九州工業大学戸畑キャンパス総合教育棟1階C-1B教室で、26aQK-10は大阪府立大学中百舌鳥キャンパスA1棟(大学本部)3階131教室で行われた。
私の自宅は、これら2つの会場のだいたい中間ぐらいに在る。
日帰りだったので、他者の発表を見る時間的余裕はほとんど無かった。
12aSC-9の会場では、到着して直ぐ会場にエアコンが効いているか確認し、あまり効いていないらしかったので、しばらく廊下で体温が下がるのを待った。
その後、会場に入室して、しばらく立ったまま最後部からオペラグラスで他者の発表を見学した。
その際に、着席している鈴木貞吉さんを見付けた。
私の発表の直前の発表12aSC-8は鈴木貞吉さんによるものだった。
この発表の質疑応答時間に、私は、次の様に質問した。
「ちょっと、いくつか思った事を、まとめて質問しようと思うんですが、冒頭にマクスウェルの電磁誘導の話が出て来てですねえ、その後はずっと力学の話に成って後半は吸着の話に成ったんですが、マクスウェルの電磁誘導が何に関係あるんだろう、という事と、あと、吸着というのは別に重力の無い所でも起こるんじゃないか、という事から、重力と吸着が何の関係があるんだろう、という様な事、それから、マクスウェルの電磁誘導をBとおっしゃってましたが、Bって普通言われるところの磁束密度の事かなあ、と思って、磁束密度と電磁誘導は違うと思います。それからあと、ですねえ、アインシュタインが質量が変換するという事を示した、とおっしゃいましたが、私は、質量が変換する、という話は聞いた事が無いので、どのような変換なのか、ちょっと教えて頂ければと、思います」
この質問についての私と鈴木さんとの問答は、次の様であった。
鈴木:う~ん、だから、特殊相対性理論では、時間が縮む、それから長さが縮む。その伸び縮みが結局相殺されて光速度一定の原理が出て来るんですよねえ。
だから、それと同し様に質量についても、そういったローレンツ変換がね、成り立つんじゃないかって言ったのは一般相対性理論ですよね。
宇田:はぁはぁ、いや、ローレンツ変換は特殊相対性理論の方ですねえ、一般相対性理論じゃなくて。※1
鈴木:うん、だから、それは、時間と長さに関しては特殊相対性理論だけれども、その、質量ね、質量に関しては一般相対性理論と
宇田:いや、その区分は違うと思います。だけど、質量の変換というのはそう言えばあったなと、思い出しました、静止質量に限った話じゃなければね。※2
あ、それから、そうですねえ、要するに、電磁気学、力学、吸着の関係ですね。
鈴木:うん、だから、ここのCって言うのは、さっき申したプラス・マイナスのCなんですよ。
宇田:「プラス・マイナスのC」のCって何なんですか、それは?
鈴木:Cって言うのは磁場ですよね?
宇田:磁場?
鈴木:うん、磁場。
宇田:はぁ。吸着の現象が起きる場所での磁場なんですか?
鈴木:いやいやいやいや、マックスウェルの電磁気学で言うと、このCは磁場なんです。
宇田:磁場?
鈴木:うん。
宇田:マックスウェルの電磁気学で言うと磁場だけれど鈴木さんの理論では何なんですか?
鈴木:私の理論では吸着槽の溶媒の質量ですよ。
宇田:溶媒の質量?
鈴木:うん。
宇田:ほう。それは、電磁気学の理論の変数を、それぞれ吸着の現象の変数に読み換えて行くと、全く同じ方程式で使える、という事なんですか?
鈴木:「うん、だから、このアイデアはね、毎月送られて来る論文があるわけですよね、雑誌の。その雑誌の論文を如何にして読もうか、ね。そのためには、グラフで言うところの2つのね、少なくとも2つの、まあ未知数って言うか、未知数に対する関数ですよね、これが与えられれば、こういう正味の吸着量を求めるところの連立方程式が解けるんだと、そういう一般化がね、可能なんだっていう事から、この理論を考え出したんですね。だから、午前中の理論にもありました様にね、う~ん、まあ、色々カラーとか、それからファクターとか、まあ、そういう形でもって、定義をするわけですね。仮定をするわけです。そいで、まあ、結論として、こういうSという、そういう場ね、スカラー場が求まりますよ、って言う事は、ま、私に言わせれば、丁度逆の関係じゃないかと思うんですよね。だから、昨日の理論では、スカラー場から出発して、それで色々展開していった理論だったけれども、今日の午前中の理論は、最終的にそういうスカラー場を、一番最後の人のアレなんか、まあiが入ってましたけどね、う~ん、虚数単位のiが入ってたけれども、まあ、そういう形に導いて、私の理論は成り立ちます、っていう事を、まあ言ってると思うんですよね。」
以上が、私と鈴木さんの問答だ。
今回もトドメは刺せなかった。
私の発表(12aSC-9)については、ohp10au-sr-1からohp10au-sr-3までを掲示しながら、口述した。
ohp10au-sr-2では、今回得られた解の2009年秋季大会での発表内容との違い、および、解くべき方程式の定義を、説明した。
今回得られた解については、
「講演概要集に書いております様に、2009年秋季大会で発表したんですが、これ(ohp10au-sr-2「解くべき方程式」)の解を求める事を発表したんですけれど、その時にはですねえ、もう少し、ここに書いてあります今回発表する解よりも、もっと特別な場合しか発表しませんでした。それから、形も級数展開の形で書いたので、何かチョッと怪しいな、という様な、まあ、ひょっとすると級数が収束しないかもしれない、という様な恐れもあって、見た感じチョッとチェックして収束はしそうだという事は見ておいたんですが、でも何かチョッと怪しいな、という感じがしてたので、もっとストンと書けないかなあと、簡単にストンと書けないかなあ、という事でやってみました。で、その2点がですねえ、2009年秋から進歩した部分なんですが、2009年秋はここ(ohp10au-sr-2「得られた解」の式中のn)がですねえn=1の場合だけやったんです。今度は一般のnについてやったんですけれど、その点はまあほとんどあまり進歩ではない、と思うんです。というのは、ここ(ohp10au-sr-2「得られた解」の式中のn)が1の場合と一般のnの場合で、あまり途中で計算は変わらないので。それから、だから、実質上は級数で書いたものを積分で書いたという所が進歩かなあ、という所ですねえ。」
と述べた。
解くべき方程式については、
「これはどういう方程式かと言いますとね、これはねえ、Φというこの汎関数に課せられた方程式という風に見て下さい。って今までの発表の続きだから今回は説明しなくて良いかとは思うんですが。でΦという汎関数に課せられた条件としての方程式でですね、Φという汎関数の変数の部分に関数が入ります。汎関数だから関数が入ります。その関数をですね、その関数のグラフの横軸の方向にεだけずらしたもの、に対するΦの値から元のものを引いたやつをεで割ってε→0の極限を取るという、ずらし微分とでも言いましょうか、そんな感じのものなんです。で、右辺はこれ特に珍しい所は無いですかね。δなんとかって、これ汎関数微分ですねえ。そうですね、右辺は特に珍しい所は無いですねえ。α定数ですねえ。これは、私が新たに導入しました定数なんですが、今回の話には特に関係ないと思います。ここ(ohp10au-sr-2上段の「ただし」に続く部分)に記号法ですねえ、□記号というか、□を使った記号の説明がしてあります。要するにχ(□-ε)という関数はtに対する値が元の関数のt-εに対する値だと。これチョッと複雑に場合分けして書いてあるのは、横軸が輪に繋いであるからなんです。横軸が輪に繋いであるのでチョッと場合分けして書いてあります。で輪の長さがTという事で。詳しくは前回の発表を見て頂きたいです。」
と述べた。
その後、ohp10au-sr-3を掲示して、どうやって解を求めたかを説明した。
その内容は、だいたい次の様であった。
Φ[χ]=F(an[χ],bn[χ])と書ける特別な場合についてのみ調べた。
この特別な場合についてはΦに対しての解くべき方程式がFに対しての
[∂2/∂ξ2+∂2/∂η2+iκ(ξ∂/∂η-η∂/∂ξ)]F(ξ,η)=0 ただしκ=2nπαm/
という方程式に直る。
この方程式はそのままでは解けないので、Fを F(ξ,η)=∫dp∫dq f(p,q)exp(ipξ+iqη) という風にフーリエ展開すると、
Fに対する方程式がfに対する
[-p2-q2+iκ(-q∂/∂p+p∂/∂q)]f(p,q)=0
という方程式に直る。
このままでもまだ解けないので、p,qを極座標に直すと解けた。
さらに、急所についてだいたい次の様にコメントした。
途中で [∂2/∂ξ2+∂2/∂η2+iκ(ξ∂/∂η-η∂/∂ξ)]F(ξ,η)=0 を
[-p2-q2+iκ(-q∂/∂p+p∂/∂q)]f(p,q)=0 に直す時に部分積分を使っていて、そこがチョッと不安だが、
最終結果の解を見てみると、(p-q平面内の)遠方で急速に小さく成る解を作れそうなので、部分積分は大丈夫だろう。
g(r,θ)は元々f(p,q)で、f(p,q)はフーリエ係数だから、gは連続関数であるべきだ。※3
だからg(r,θ)=g(r,θ+2π)であるべきだ。
この事から、(r2/κ≠整数)なるrに対してはγ(r)=0であるべきだ、と言える。
すると、γはデルタ関数状に成る。
その点が不安なので、フーリエ積分を実行して(解に成っているかを)直接確認したいが、それが出来ない。
γがデルタ関数の微分やデルタ関数の2階微分の場合については、(fがp-q平面内の)遠方で急速に小さく成らないので、
途中で使った部分積分が危なく成るので駄目だろう。※4
前回の発表(2009年秋季大会13pSH-3)では、
[∂2/∂ξ2+∂2/∂η2+iκ(ξ∂/∂η-η∂/∂ξ)]F(ξ,η)=0
が解けなかったので、解を級数展開で表し報告記事に、誰か解けたら教えて下さい、という風に書いておいたのだが、その後2010年05月09日に自分で解けた。
その事がwww.GrammaticalPhysics.acのNewsに掲示されている。
けれど、そこではまだ、(r2/κ≠整数)なるrに対してはγ(r)=0であるべきだ、という条件に気付いていない。
この条件に気付いたのは、講演概要集執筆中だった。
| 講演概要 |  12aSC-9 |
日本物理学会講演概要集 第65巻 第2号 第1分冊 5ページ。 English |
|
| OHP |  OHP-sr-1 |
 OHP-sr-2 |
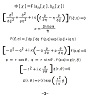 OHP-sr-3 |
質疑応答時間には、まず、鈴木貞吉さんから、
「やっぱり、結論というか、何かこう、グラフにでもしないと、自分のやっている計算がですねえ、自分では解けたつもりでも、それが正しいかどうかの判断をするね、そういう手掛かりってものが無ければ、やってもなんか、意味が無い様な気がするんですけどね。ただ自分でそれが解けたんだという自己満足に終わっちゃう様な気がするんですけどね」
というコメントを頂いた。
これに続いての私と鈴木さんとの問答は以下の様であった。
宇田「ほう。グラフにしようとは思わなかったですけれど、これから帰った後、グラフに出来るかどうか検討してみたいと思います。だけどまあ、グラフにしたところで、しなかった場合に比べて、よりキチッと解けているかどうかが確認できるとは思わないですが。どちらかと言うと今回の場合は、式で確認した方が確実だと思うんですが、一番やりたい確認は、最後のこの結果(ohp10au-sr-3の最後の式)をどんどん上に遡って代入して行って、ここ(ohp10au-sr-3の第2式)を確認するんです。これ(ohp10au-sr-3の第2式)が直接確認できればまあ安心なんですが、それが出来ないんですよ、今回。という事をさっき申し上げましたが」
鈴木「だからそのg(r,θ)ですよね。私の場合は結局実験データが元に成るわけですよね。だからコンピュータの基本ソフトと言うか、それは吸着力と言うのは結局万有引力のエネルギーだと、そういうもので基本ソフトを作る事が出来るんですよね。だけど、そのg(r,θ)を例えばコンピューターに乗せようとしても、それは不可能じゃないかなあ」
宇田「g(r,θ)をコンピュータに乗せる、と言うと、どういう事なんでしょう?例えば、コンピュータのプログラムの、この関数に従って数値計算か何かに、コンピュータにやらせる、という事ですか?」と聞き返した。※5
鈴木「だから、コンピュータ上で回転している画像って言うか、それを描こうとした場合に、何かもう一つ対象と成るものがね、無ければ、何の意味も無い様な気がするんですけどねえ」と説明した。
宇田「何の意味も無いと言って、どう言うんですかねえ、物理学の教科書なんかに載っております式にですねえ、似たような式は色々あると思うんですが、まあ全く同じは無いかもしれないけれど、それらについては全部鈴木さんの言ってる批判がですね、まあ仮に成り立つとして、そしたら、それらは全部何の意味も無いのか、という事でね。そんなはず無いでしょう。それからグルグル回ってる円と言うの、これ何か図的に、私の今回やりました計算を図の様なもので表すとしても、グルグル回った様な円というのは到底描きそうに無いと思います、私は。もっと違うものに成ると思います。」
鈴木「描けないと思いますよねえ」
宇田「いや、描けないんじゃなくて、端からそういうものは目指さないはずです。非常に的外れなので、それは。」
次に別の人から、円環時間を使う動機は何か?という意味の質問を受けた。
これに対して私は
「これはねえ、技術的な問題でですね、時間軸を輪に結ばなかったらよう解かんわ、というやつで、解けないわあ、と言うか、処理が出来ない。で、じゃあ輪に結んでしまったら、非現実的な仮説を入れてしまっている事に成って、そんなものでいくら計算が出来てね、答えが出て来てもね、現実とは関係の無い答えがたくさん出て来てるだけだから意味が無い、という批判は考えられると思うわけです。しかしですねえ、輪に結んで、その輪の長さを無限大にする極限を取ったら、輪に結んでない時間軸の場合と考える事は出来ないかと、そういう見地もあると思うんです。だから、あながち、現実とは関係ない無意味な事をやってる、とは思わないんですよ。という事でまあ、円環時間でやるというのは技術的な理由です。あとプラス、それでもたぶん意味があるだろうという、その2つぐらいの理由ですかねえ。」
と答えた。
これについては、日本物理学会2009年秋季大会報告記事の13pSH-3部分に詳しい説明があります。
特に、円環時間は量子力学で用いられる周期的境界条件に類するものだ、という説明が、そこには含まれています。
私の文法主義についてのご意見ご感想はwww.GrammaticalPhysics.ac またはWooder!掲示板にお寄せ下さい。
26aQK-10では、講演概要の文章をOHPで掲示して、それを読み上げながら要所要所で補足説明した。
座長さんからマイク使用について発表中や質疑応答時間に何度か指示があって、それに従ったが、これが結構話の流れを断ち切って負担だった。
面白く言うと、次は「皿回しをしながら発表して下さい」と言われるのではないか、と思った。
講演概要に対しての補足説明として私が口述した内容を、以下に書き起こす。
冒頭の「その事を私自身の体験実感に基づいて述べる」という部分まで読んだところで、
「勉強の苦手な生徒の高大接続だけでなく勉強の得意な生徒の高大接続にも不連続性がある、という話です。
もともと不連続だったのに、ゆとり教育で、その不連続性を増大させた事は、破壊的であり、ほとんど悪魔の所業だと思います。
バベルの塔建設に対する神の妨害を連想します。
だから、ゆとり教育は高等教育を社会の蚊帳(かや)の外に置こうとする動きだったのではないか、と私は疑っています」と付言した。
「大学初年次の学習内容は・・・格段に難しい」という部分について、「難しいので先生も100%理解しているわけではない場合があると思います」と付言した。
「大学では、授業も教科書も、高校までより解説が不親切(突き放した感じ)に成る」という部分について、「これについては、演繹過程の細部が省略される事や、進度が早い事が挙げられる、と思います」と付言した。
「高校までは・・・だが、大学では・・・学生の何をどれだけやるかの選択が投機的に成りがち」という部分について、「さらに細かく見て行きますと」と言って、ohp10au-13-3を掲示して補足説明を行った。
「何をどの程度出来る様に成れば良いのか学生に分かり難い」という部分について、「これは、まあ単なる言い換えですが、何もかもと考えてしまうと処理し切れません」と付言した。
「教科書・参考書の選択が難しい」という部分について、
「これについては、例えば、量子力学の勉強としてメシアの教科書を隅から隅までキチンと読もうとすると他の事が出来なく成ります。
私は、東京神田神保町の書泉グランデという書店で偶然友人に会った折に、シッフの教科書を薦められて、読んでみたらこれは一応当たりでした。
この本の書籍紹介欄でベルグマンとメラーの相対性理論の教科書を知り、メラーが当たりだった事も考えると、
もしその偶然が無かったら、私の勉強はさらに何年遅れていたか分かりません。
何とも危なっかしい限りです」と付言した。※6
「厳密でない論理展開に対して寛容になる・・・全責任を負う必要は無い」という部分について、
「これは数学の外注化や正当化の先送りであって、インチキの許容ではありません。
大学初年時に限らなければ典型例はデルタ関数の使用だろうと思います。
δ関数が出て来たからと言って超関数を学ぶ必要までは無い、という事です。
大学初年時ではないけれど、私は「超関数の理論」という数学書を買ってしまいました。
読まなくて良かった、と思っています。
使う数学に高校までの透明度を要求すると処理し切れなく成ります。
高校でのロピタルの定理の扱いの勢いで行くと駄目だという事です。※7
寛容を宣言しなければ、責任感の強い学生が厳密の森に迷い込んで、出て来た時には浦島太郎の様に成ってしまう恐れがあります」と付言した。
『要求されるのは「分かった」までで「解ける」は要求されない』という部分について、
『これについては、もの自体が難しいので、大げさに言うと何か解けたら即業績です。
「解ける」は定期試験で試されますが、これも「解ける」の試験ではなく分かったかどうかを調べるためのものでしょう。
「解ける」は要求されない、という事は、演習と名の付く授業の内容が講義だったりした事にも現れています。
高校では教科書読解の後、問題集で応用力を付けますが、大学では教科書読解で終わりと考えるべきです。
教科書読解の過程で、省略されている演繹過程を自分で埋める事が十分な問題演習に成ります。
高校までの調子で「教科書は序の口、問題集が本番」と考えると失調します。
私は、大学へ入った後も問題集を色々やって学習が何年も遅れました。
特にマグロウヒル大学演習シリーズの微積分(上)(下)を自力でほぼ全問解いた事に、多大な時間を取られました。
無意味とは言えませんが、その分、高学年向けの勉強に費やせる時間と体力が随分減りました』と付言した。
「要求されるからする、要求されないからしない、という態度を必ずしも私は奨励しているわけではない」という部分について、
「目標を自分で決め、その目標達成のために最適の勉強が標準と異なっていても、気にしない、という態度はありだと思います。
けれど、何が標準かを良く知った上でそうするのでなければ、無謀だと思います」と付言した。
その後、ohp10au-13-3を外してohp10au-13-2を掲示して、講演概要本文の説明に戻った。
「真面目派の新入生は高校の木から大学の木へサーカスの様に飛び移れるか否かの瀬戸際に立たされる」という部分について、
「私が学生だった当時の新入生は、大きく分けて、真面目派と非真面目派に分かれていたと思います。
真面目派は、大学ではしっかり勉強するつもりの学生で、非真面目派は、大学ではしっかり遊ぶつもりの学生です。
(この部分で笑い声を頂いて嬉しかったが間を取る時間的余裕が無かった)
その他、体育会系、というのもありますが」と付言した。※8
「大学初年次教育を微調整して学生に飛躍を要求しないシームレス高大接続を実現すべきだ」という文中の「微調整」について、
「微調整で良いと思います。少し手直しするだけで、大筋においては、既存のもので良いと思います。
物理学正典の補足説明欄の様なものを整備する事で達成されるのではないか、と思います。
裁判の判例や医学の臨床例の辞典みたいなものを作る気持ちで臨めば良いのではないかと思います」と付言した。
『この友人が「いくら宇田君でも」という言い方をしている事にも現れている事だが』という部分について、
『私が優等生だったか否かの客観性よりも、この友人が「優等生にも分からないはずだ」という評価をその授業の内容に加えている点に注意してください」と付言した。
| 講演概要 |  26aQK-10 |
日本物理学会講演概要集 第65巻 第2号 第2分冊 363ページ。 |
|
| OHP |  OHP-13-1 |
 OHP-13-2 |
 OHP-13-3 |
質疑応答時間には、最初しばらく待っても質問やコメントは出なかったので、座長さんが私に補足する事は無いか尋ねた。
そこで私は、ちょっとしたエピソードを紹介した。
その内容を以下に書き起こす。
『私がですねえ、大学の2年目の時に、2年目が必ずしも2年生じゃなくて、まだ1年生だったんですが、ある演習の授業、何の演習・・・電磁気学演習だったかなあ、大学院の生徒の方が先生をしておられたんですが、その人が力学の問題の事をですねえ、「あなた積分できますか」といった類の問題だ、という事を、おっしゃったんですよ。
で、私はその当時それまで、もうほとんど「力学の問題命」みたいな感じで力学の問題の問題演習、先ほど具体例を挙げましたのは微積分の話なんですが、数学の話なんですが、物理で言うと力学の問題ばかり解いていたもんですから、それを聞いて豪く心の中では反発したんですが、今考えてみるとですねえ、全くその通りでですねえ、ニュートン力学の問題を与えて、それの解を求めよ、という問題は、本当に全く、この、「あなた積分できますか」といった類の問題でですねえ、こういう部分は、どちらかと言うと、物理学と言うよりは数学に属する問題なのでですねえ、・・・
これ、どこに対するコメント言ってるかと言うと、先ほど数学の外注化という様な所が出て来ましたが、・・・
あれ?あ!これ(OHP)に書いてあるわけじゃないんだ。
口で読んだだけですね。
はいはい、口で読んだだけです。
口で読んだのは・・・
「学習のルールが変わる」の最初のこれ(ohp10au-13-3「厳密でない~必要は無い」を指示しつつ)に対する口でだけ述べたコメントの中に「数学の外注化」という言葉が入っておりましたが、その観点から言うならば、
まあ、微分方程式を解くという作業にあまりのめり込むのはですねえ、その分だけ物理学に対する理解が深まったという事ではない、という事でですねえ、まあ、それを嘲笑するかの様に言うと、その、力学の問題というのは「あなた積分できますか」といった類の問題だと、まあ、こういう逸話をちょっと紹介しておきたいと思います』
その後、
「何が言いたいのでしょうか?良くわからない・・・
大学の初年度の物理の授業をもうちょっと易しくして下さい、という意味なんですか?」
という質問を頂いた。
これに対して私は、
『うん、そういう言い方も出来ると思いますね。
はい、そういう言い方も出来ると思います、ええ。
けど、あと、その後、もう少し言うと、この中に入ってたのは、もう少し情報を与えてください(※9)、というのは有るかもしれない。
例えばですねえ、授業によってはですねえ、先生が授業の最初に、こういう参考書がありますよ、というのを紹介して下さる人も居るんですが、授業によっては、そういうものを一切紹介せず、生徒の間で噂が飛び交っていて(※10)、で、「宇田君、あの、この教科はさあ、この本が良いんだってさ」と、で、それだけが頼りと、そういう授業もまたあるわけなんですよ。
だから、情報を与えてください、というのはありますねえ」
と返答した。
続いて座長さんから
「で、あれですか、そうすると、あまりあの学生も居ますけども、例えば微積分で本当にその、微積分の別の本を買って一所懸命やりますよねえ。それは駄目なんですかねえ?」
という質問を頂いた。
これに対して私は
「う~ん、やり過ぎると、残念でしたね、という所かなあという、う~ん。まあ、やり過ぎた事によって、次はやり過ぎない様にしよう、というのを学ぶというのも大切だと思うんですが」
と返答した。※11
最後に別の人から
「先ほどの発表のコンピテンシーという能力が、ある意味問われているのかもしれないなあ、と思って聞いていました」
というコメントを頂いた。
私は、コンピテンシーの意味が分からなかったので、
「コンピテンスィーというのは競争力ですか?」
と聞き返した。
その時の会話を以下に書き起こす。
相手「先ほどの発表のコンピテンシーというね、区別できる能力と書いてありましたが、そういう風なものが改めて大学1年生、初年級で問われている、という気はしなくないですか?」
私「う~ん、情報が欠乏している方が、そういう能力が鍛えられるという?」
相手「まあ、そうは言わないんですけども、そういう能力が必要だな、という・・・多くても困るし、少なくても困るし」
私「そうですね」
以下は会場での発言ではありません。
※1 「はぁはぁ」は、この後の「質量の変換というのはそう言えばあったなと、思い出しました」と、呼応しています。
※2 私がここで思い出したのは、普通は、運動する物体の質量が増加する、という言葉で表現される法則で、普通はこれを質量の変換とは言わないが、同じ物体を異なる座標系で測れば速度が異なり、それ故に速さに依存する質量も異なるので、質量の変換と見なす事も許されるか、と会場では思ったが、今考えてみると、やはり、これは質量の変換ではない。
※3 これは正確ではない。正確には、連続関数であるべきなのはfだ。そうするためにgに付与される性質は見ての通り周期性だ。
※4 この発言は表面的には間違っている。
γがデルタ関数の微分やデルタ関数の2階微分を含んでいても、明らかに、r→∞でg(r,θ)が急速にゼロに近付く様にする事は出来る。
しかし、その様な場合にはgが、フーリエ積分においてexp[r2θ/(iκ)]をrで微分した因子を生じさせ、その事が部分積分を破綻させるだろう、との見通しを念頭に置いて、しゃべりました。
本当にそうなのかは未確認です。
※5 この部分では、私は助詞「の」「に」を誤用しています。これは私の癖ではなく、後に続く文を誤って予想したためです。
※6 量子力学の話を持ち出してしまったので、誤解を防ぐために断っておくが、私が受講した回の鈴木公先生による量子力学の講義は良い講義だった。
この講義では、初回に鈴木先生による書籍紹介があった。
個別的には、他にも良い授業はあった。
また、ここでは、教科書の選択の難しさを説明しているのであって、授業の良し悪しを論じているのではない。
因みに、量子力学の教材として私は量子力学正典というものを書いておりますので、ご利用ください。
※7 大学の微積分で習うε-δ論法の方が厳密だが、物理学で用いる全ての数学的事項をε-δ論法で証明する、なんてのも、もちろん、厳密の森→浦島太郎だ。
しかし、ε-δ論法なんて知らなくて良い、というわけではなく、ε-δ論法も、ここぞという時に使うと、役に立つ。
※8「飛び移りの内容としては、ルール変更を自分で感じ取る事と、予備知識の欠如を自力で補う事が、挙げられると思います」というコメントを事前にメモしておいたが、読み忘れた。
講演概要の「実際多くの学生が飛び移り損ねて大学には出席するだけの状態に陥っていただろう」という部分について、「卒業した後に学生はもう受験しないので高校ほどには学生の学力に責任を持たない、という体質が大学にはあると思います。非真面目派の学生に厳し過ぎるのも良くないけれど、真面目派の学生が挫折しない様に出来ればと思う」というコメントを事前にメモしておいたが、これも読み忘れた。
※9 講義だけで情報が無いと、<冗談>俺の板書を写すの間に合わんかったヤツは地獄へ落ちろ</冗談>といった感じに成るし、どの講義を選択すべきかの直接的な指針も得られない。
私が東京理科大学の学部4年生だった時だったか、友人に誘われて東京大学の大学院のガイダンスに行ってみた事がありました。
その時に、担当の先生に「博士号を取るまでに平均して何冊ぐらい本を読むんですか」という質問をしたら、その先生は、一瞬答えに詰まった後で「君、その質問はおかしいよ」と言って、大学院は研究をする所であって学習をする所ではない、という意味の事を、機嫌悪そうに説明してくれました。
それを聞いた時の私の心境の変化は、ひょっとして→やっぱりな、でした。
これなんかも、書籍情報については指導側は口が重い、という事の現れだと思う。
因みに、私は大学院には行っていません。
※10 噂の内容はいつでも正しいわけではなく、例えば、「線形代数なんて数の遊びだ、と先輩が言ってたよ」という噂を聞いた事があるが、つまり、線形代数は1年生の数学で出て来た後は高学年の物理学では2度と出て来ない数学のための数学だから、その場しのぎで対処するのが賢明だ、という意味の噂を聞いた事があり、それを聞いた時には「それは言えてるかも」と思ったのだが、この考えは間違っていて、線形代数の抽象ベクトル空間論は量子力学を深く理解するためには必須だ、という事が、後で量子力学を勉強した時に分かった。
※11 全体としては、やればやるほど良い、いくらやってもやり過ぎるという事は無い、と思う。
しかし、部分については、部分をやり過ぎると、やり過ぎる部分によっては、その事が全体としての成果を減じてしまう。