since 2003
イレコナビ サイトマップ
日本物理学会2004年秋季大会で発表完了。
講演概要は以下の通り。
発表に用いたOHPフィルムも下に掲載しておく。
まず15aZA-1「砂川重信著「理論電磁気学」正誤表」について。
分量が多かったので、講演概要に書いてある事は適宜省略する、と断った上で講演した。
紀伊国屋書店の許可を得て発表するわけでもないし紀伊国屋書店の代理として発表するわけでもなく僕が独自に発表するものである、と断った上で本論に入った。
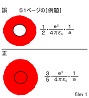
まずfilm-1を提示して、51ページの例題では一様帯電球の外部の電場のエネルギーが求められているが、内部の電場のエネルギーまで合わせたものを求めるべきである事を指摘。
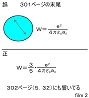
次にfilm-2で301ページのWを求める途中の計算にミスがある事を指摘。
ミスを修正した結果得られる正しいWの値を提示し、それがクーロン・ポテンシャル・エネルギーの総和である事を述べるとともに、51ページの例題を修正した結果に、正しいWの値が一致する事、を指摘。
次にfilm-3を提示し、電流・電荷の無い場合についての、すなわち自由電磁場についての、電磁ポテンシャル（ベクトル・ポテンシャル）について、砂川の本で考え落とされている項をフーリエ係数のレベルで挙げ、それらがローレンツ・コンディションによっても除外できない事を指摘。
デルタ関数が4つとも微分されている項はローレンツ・コンディションによって除外される事も、コメントした。
次はfilm-4を提示して4次元のグリーン関数をダイレクトに求めるためのフーリエ係数を紹介した。
この係数は僕が自分で編み出した。
この係数についてグリーン関数のフーリエ係数を決める条件が満たされている事を確かめるのは容易である、とコメント。
次は、荷電粒子が作る電磁場からその粒子自身が受ける力（自己力）を考えに入れた場合の運動方程式としてfilm-5を提示し、film-6の最初の式を相対論的なものに修正するとすれば、一見レッドのアンダー・ライン部分が必要では無いかに見えるが、この部分は必要であること、およびその理由として砂川が挙げている式(4.12)が理由としてふさわしくない事を発表。
式(4.12)では右辺が自己力を全て含んでいるのに対して、401ページ冒頭では自己力の一部は左辺に移項されているからだ。
また式(5.20)の提示が天下り的である事も砂川の本の欠点ではないかと思う。
僕は砂川の理由付けとは違う理由付けをして見せた。
それがfilm-6とfilm-7であって、コンセプトは、v＝0の瞬間にfilm-6の最初の式に一致するような相対論的方程式を求めよう、というものだ。
レッドのアンダー・ライン部分の必要性は、方程式の時間成分（film-7の第二式）から見て取れる。
次にfilm-8を提示したが、これについてはfilm-8に書かれている通りである。
僕は論文を良く読んだわけではないので皆さんが自分で検討してくださるように、とコメントした。
次にfilm-9を提示したが、これについてもfilm-9に書かれている通り。
これについては、そう考える事が出来る決定的な証拠までは僕はまだつきとめていない、とコメントした。
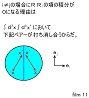
次にfilm-10とfilm-11を提示したが、これについても、フィルムに書かれている通り。
あえて補足するなら、film-11で考えられているペアーは、球の中心を通り第 i 軸に垂直な平面に関して面対称なペアーだ。
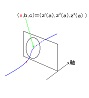
最後にfilm-12を提示しノーテーション（記法）を正した。
レッド・ラインがライト・コーンで、ブルー・ラインが粒子の世界線。
nもαもt0'の関数ではなくxとtの関数であるのに、砂川の本の書き方は、その事を正しく反映した書き方になっていない。
少し時間不足気味だったので、ホームページを見てください、と最後に言っておいた。
アマゾンに僕が書いているレビューも参考にしてください。
| 講演概要 |  15aZA-1 |
日本物理学会講演概要集 第59巻 第2号 第2分冊 329ページ。 |
|||||
| OHP |  OHP-13-1 |
 OHP-13-2 (film-1) |
 OHP-13-3 (film-2) |
 OHP-13-4 (film-3) |
 OHP-13-5 (film-4) |
 OHP-13-6 (film-5) |
 OHP-13-7 (film-6) |
 OHP-13-8 (film-7) |
 OHP-13-9 (film-8) |
 OHP-13-10 (film-9) |
 OHP-13-11 (film-10) |
 OHP-13-12 (film-11) |
 OHP-13-13 (film-12) |
||
30pSC-8「ガウスの法則を補完する3つの法則」については、聴講者が10人程度しか居なかったので既知事項かどうか十分には確認できなかった。
少なくとも聴講者からは既知事項であるとの指摘は無かった。
講演概要に書いてある事に付け加えて、時刻t＝aで粒子の速度がゼロになる場合の積分結果の予想を述べて、どうせこうなるだろうと思うが証明は僕はやる気が無いのでやりたい人はやってください、とコメント。
その後、ローレンツ変換を使って証明する方法の概略をヒントとして付け加えた。
電荷密度分布と電流密度分布が連続の場合についてどうなるかの予想も述べておいた。
これも僕は証明していない。
| 講演概要 |  30pSC-8 |
日本物理学会講演概要集 第59巻 第2号 第1分冊 10ページ。 |
||
| OHP | 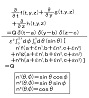 OHP-sr-1 |
 OHP-sr-2 |
 OHP-sr-3 |
 OHP-sr-4 |
発表時間に余裕があったので座長さんから「補足は無いか」と言われ量子力学についてコメントした。
量子力学の実験による最も直接的な確認として日立の外村さんによる実験が知られているが、量子力学は時刻指定の実験に対する予言しか行わないのに対して外村さんの実験はx座標指定の測定なので外村さんの実験は量子力学の直接的検証とは言えない事、量子力学においては運動量の測定というものが良く定義されていない事、つまり、運動量を決める波動関数の波長は1個の粒子を1回限り時刻指定で測定しても分からない事、をコメント。
空き時間に僕のセッションの1つ前のセッションの座長さんと話をした。
座長さんは毎回違うが、今までの経験から、座長さんはみな若くて、それで居てすべての発表に頭がついて行くような優秀な方だ、と分かっている。
僕は座長さんに、近い将来グラスマン変数の表示を発表しようと思う旨を伝え、そういうものが物理学の世界では既に一般に知られているか？と尋ねた。
すると「知られていると思います」という答えが返って来た。
さらに、教科書レベルで知られているのか論文レベルで知られているのかを尋ね、「教科書レベルです」という答えを頂いた。
それを聞いて僕はその発表をやめようと思い、その旨を座長さんに伝えた。
後で念のため、どの教科書か尋ねてみた。
すると「ワインバーグなどに記述があると思います」という答えが返って来た。
僕はグラスマン変数が長年理解できなかったのでグラスマン変数の説明の詳しい教科書を探しスワンソンの本に出会いこの本の説明を見たがやはり説明が不十分だったので仕方なくグラスマン変数の表示を自分で考え出した事、スワンソンはグラスマン変数の説明にまるごと1章を費やしているがこの詳しさは他に例を見ない事、を述べた。
すると座長さんは「確かにグラスマン変数の説明に1つの章を割り当てるほどグラスマン変数の説明が詳しい本は無い」と述べた後、「グラスマン変数に1つの章を割り当てるほど詳しく解説する必要を感じないし、そもそもグラスマン変数の表示とはどういう意味なのか分からない」と述べたので、僕はやはり表示は知られていないなと思い「でしょ？でしょ？やっぱり僕が発表する意義があるようです」と述べて対話は終了した。
 |