
since 2003
イレコナビ サイトマップ
ローレンツ変換
このページでは前ページ「ローレンツ収縮、および運動する時計の遅れ」よりワンランク上を目指すよ。
前ページでは図解だったが、このページでは式とグラフにチャレンジだ。
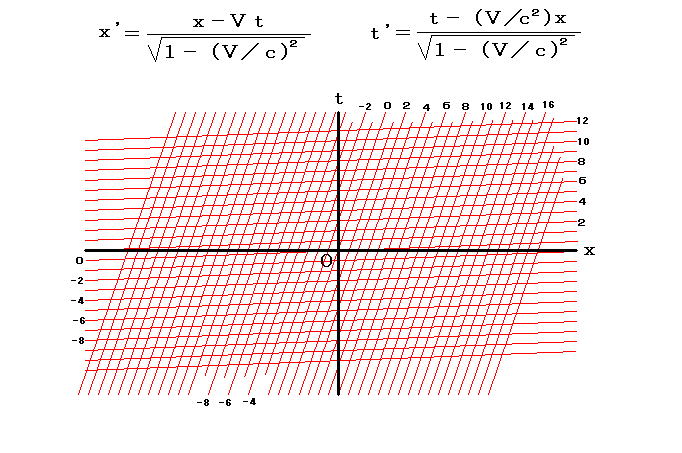
下に貼り付けてある式とグラフは「ローレンツ変換」を表している。
ローレンツ変換とは、静止している人が測定した場合に得られる位置 x と時刻 t を運動している人が測定した場合に得られる位置 x' と時刻 t' に関係付ける式のことだ。
Vは運動している観測者の運動速度を、c は光速を表している。
簡単のため物理的事件は全て x 軸上で起こるものとする。
静止している人が測定すると時刻 t に位置 x で起こった事件は、下式で与えられる t' と x' を用いて、運動している人が測定すると時刻 t' に位置 x' で起こったものとして観測される。
ただし、運動している人が位置測定に使う x' 軸は x 軸と重なったまま等速運動し続け、時刻 t=0の瞬間に丁度 x' 軸の原点は x 軸の原点を通過するものとする。
さて、ここに挙げた関係式(ローレンツ変換)は頭の中だけで考えて得られるものではない。
「光速不変の原理」だけから得られるものでもない。
究極的には実際に測定してみて成り立つことを確かめなくてはいけないものだ。
ではあるが、ローレンツ変換の式が正しいことを直接測定して確かめた、という話は聞いたことがない。
では何故、みんなこの式を信用するのか?
それは、この式が成り立つと仮定して話を進めて行くと直接測定可能な様々な現象についての測定結果と理論値が一致するからだ。
物理学って、こういう手口を使うんだよ。
実験結果から原理を導き出すんじゃあなくて、これが原理なんじゃあないかなあ、というものをまず仮説として打ち立てて、それが正しいと仮定して論を進めて行くと実験・観測結果に一致する結果が得られる。
それを理由にして最初に打ち立てた仮説が本物の原理なんだって認定するんだ。
ローレンツ変換の式もそうやって認定された物理学の原理なんだ。
ところで式を見ても分からないだろ?
ルートの中に2乗があったり、そのルートが分母になってたり、チョッと厄介だよね。
この式は数学の事をもっと勉強してから見ないと難しすぎる。
宇田先生だって中学校で習う数学の知識だけを武器にしてこの式を見るとわけが分かんなく成っちゃうんだよ。
だから式の下にグラフを書いておいてあげたからね。
ローレンツ変換は高校数学で言うところの一次変換だ。
じゃあ、グラフの見方を説明するよ。
まず、グラフはローレンツ変換の式(今の場合2つの式から成る)を表しているという事を確認しておくよ。
ローレンツ変換の式とグラフはどうやって関係付けられるか?
要するに x と t が与えられたときに、それに対応する x' と t' が求まりゃあ良いんだろ?
グラフ中には2種類の赤線群があるぞ。
t 軸に平行に近いものと x 軸に平行に近いものの2つだ。
t 軸に平行に近い赤線を「時間的赤線」と呼び、x 軸に平行に近い赤線を「空間的赤線」と呼ぼう。
時間的赤線に添付してある数が x' の値で、空間的赤線に添付してある数が t' の値だ。
よし、行くぞ!
x と t が与えられた。
するとグラフ内の一つの点が指定される事に成るよな?
そこを通る時間的赤線に添付された数が、与えられた( x , t )に対する x' の値だ。
また、そこを通る空間的赤線に添付された数が、与えられた( x , t )に対する t' の値だ。
へ?それだけかって?
うん、それだけだよ。
簡単すぎるか?
そんなことはないだろう。
よく見て見ろよ。
時間的赤線が t 軸に平行でないのはまだ良いとしても、空間的赤線が x 軸に平行でないのは妙だぞ。
この事情があるために t の値が同じでも x の値が違えば t' の値が違うって事に成る。
これって前ページに出て来た「同時刻の相対性」なんだよね。
まだ終わりじゃないぞ。
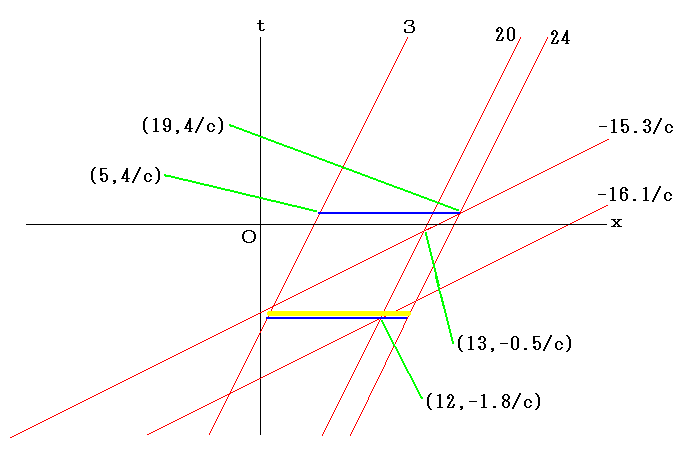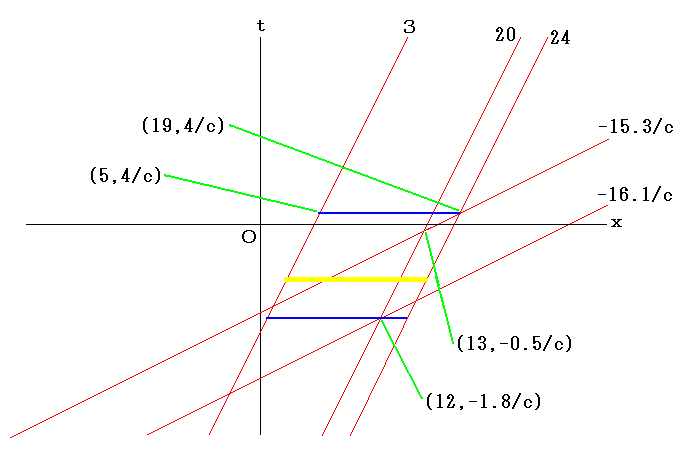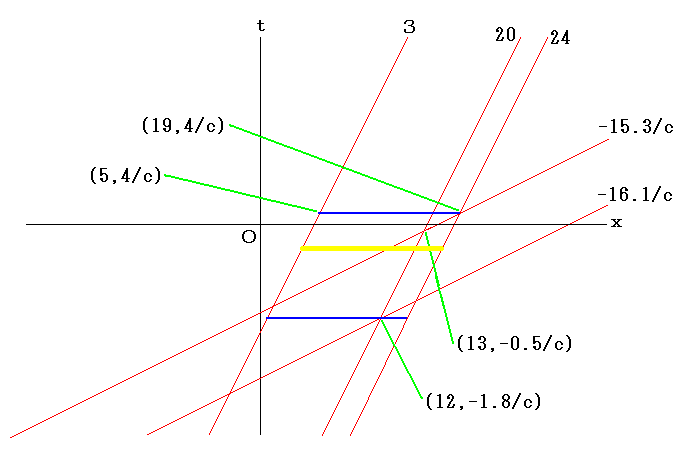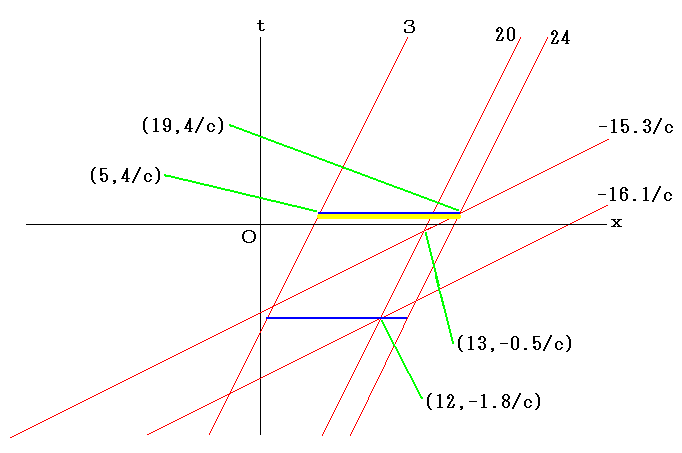
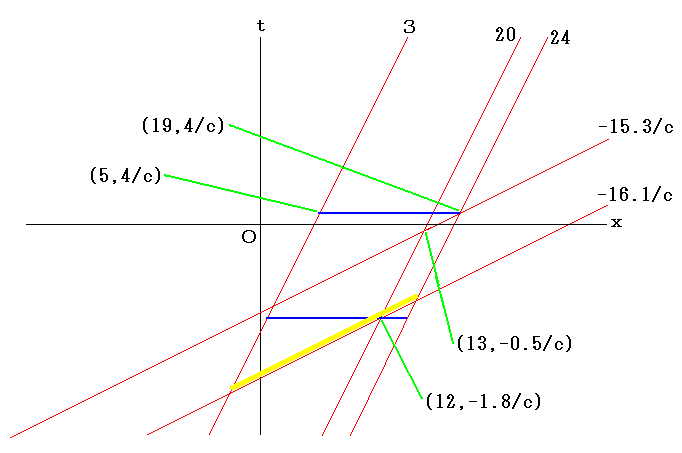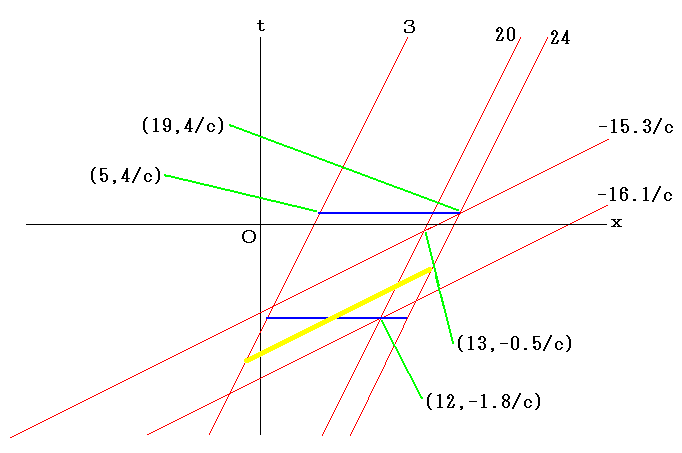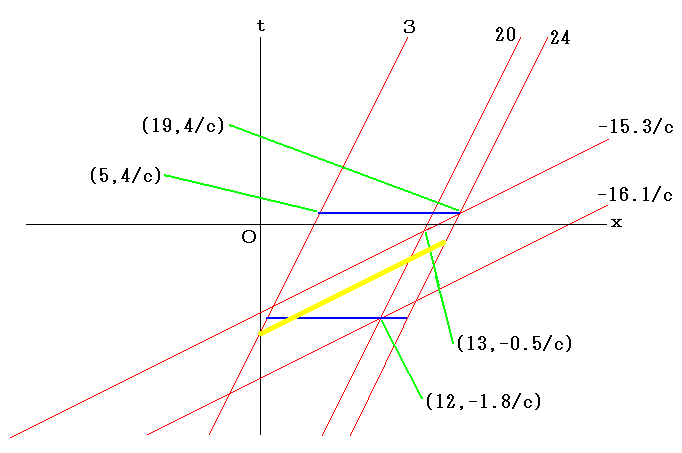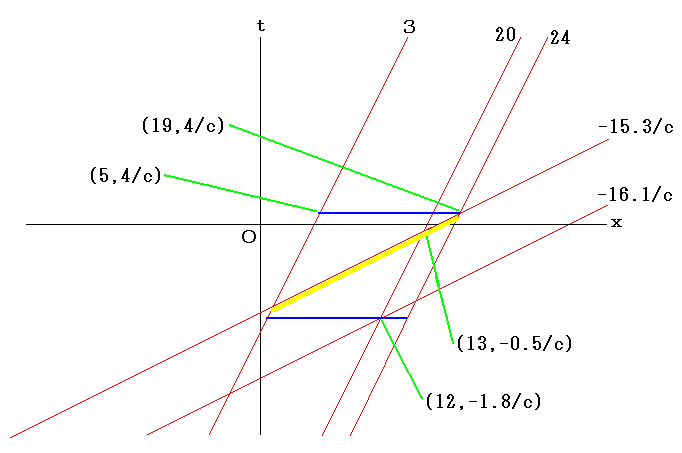
この場合、ローレンツ変換を表すグラフの一部分は以下のようになる。
前ページの上側の物差し(右向きに運動し続ける物差し)の点3から点24までの区間を静止している人が観測する(前ページ下側の物差しとそれに固定された時計で計る)と、それは下図の黄色いバーのように運動し、その長さは常に19-5=14だ。
下図においては光が下の物差しの点12を出てから点19に到着するまでの間についてのみ、上の物差しの点3から点24までの区間を黄色いバーで表している。
なお、数値は概数であって正確な値ではない。
下図もやはり光が上の物差しの点20から発射されてから上の物差しの点24に到着するまでの間だけを取り出して描写している。
これは上図で問題にしているのと同じ事象から同じ事象までの時区間だ。
上側の物差しで計ると、自分で自分を計ってるんだから当然と言えば当然だが、上側の物差しの点3から点24までの区間は運動しない。
このことは時間的な赤線3と時間的赤線24の間に黄色いバーがピッタリと収まったまま運動する事から分かる。
黄色いバーの移動に伴って、それに重なる空間的な赤線が変化する(時間が経過する)のみである。
上の物差しに固定された人が測定すると黄色いバーの長さは24-3=21であり、これは下の物差しに固定された人が計った値14よりも大きい。
ここに至って前ページで述べておいた「ローレンツ収縮」は「ローレンツ変換」から導き出されたことになる。
「ローレンツ変換」の特徴は「ローレンツ収縮」だけではない。
下のグラフをよく見てくれ。
上側の物差しの点20が下側の物差しの点12を通過してから点13に達するまでの時間を静止した人が測定すると
(-0.5/c)-(-1.8/c)=1.3/c であるのに対して、同じ現象を上側の物差しに固定された人が測定すると結果は
(-15.3/c)-(-16.1/c)=0.8/c となり、上側の物差しに固定された人が測定した結果の方が小さな値となる。
これで「運動する時計の遅れ」もローレンツ変換から導き出された事に成る。
「同時刻の相対性」「ローレンツ収縮」「運動する時計の遅れ」の3つは「ローレンツ変換」の最も有名な特徴であり、我々はここまででそれら全てを「ローレンツ変換」の公式から導き出したことになる。
「ローレンツ変換」についてはこれ以上特に言うべき事はない。
ここまで理解できた人は「ローレンツ変換が分かった」と考えてもよろしい。
「トーマス歳差」なんてのもあるんだけど、現段階で「トーマス歳差」まで説明するのは無理だ。
おっと、忘れてた。
ローレンツ変換にはもう一つ重要な特徴があるんだ。
それは「時間的隔たりはローレンツ変換を受けても時間的隔たりに、空間的隔たりはローレンツ変換を受けても空間定隔たりに、光的隔たりはローレンツ変換を受けても光的隔たりに写される」という特徴だ。
2つの事件が
( x , t )=( a , b ) と ( x , t )=( e , d )で起こったとし、
( x , t )=( a , b ) に対しては ( x' , t' )=( a' , b' )
( x , t )=( e , d ) に対しては ( x' , t' )=( e' , d' )
とする。
2つの事件が時間的に隔たってるとは|a-e|<c|b-d|が成り立つことを言い、
2つの事件が空間的に隔たってるとは|a-e|>c|b-d|が成り立つことを言い、
2つの事件が光的に隔たってるとは|a-e|=c|b-d|が成り立つことを言う。
ローレンツ変換は
|a-e|<c|b-d|ならば|a'-e'|<c|b'-d'|であり、
|a-e|>c|b-d|ならば|a'-e'|>c|b'-d'|であり、
|a-e|=c|b-d|ならば|a'-e'|=c|b'-d'|である、
という特徴を持っている。
へ?そんな?って思うでしょ?
でもそうなんだ。
じゃあ何があるか?
「特殊相対論的」理論ならある。
というわけで、前ページでも言ったように「ローレンツ変換」を理解したからといって特殊相対性理論を学び終えたと考えちゃあいけないよ。
「物理理論が特殊相対論的だ」とはどういう意味か?とか、「特殊相対論的」理論を具体的に取り上げてそれがちゃんと「特殊相対論的」に成っている事を確かめてやろう、という方向へ勉強は進んで行くんだ。
この続編としてそこまで行けるかどうか分からないけど、やってみるかもしれないから楽しみにしててね。
この辺で、これまで学んだ事のまとめとして、特殊相対性理論についての僕の「悟り」を伝授してあげます。
この「悟り」は特殊相対性理論の全てを表現し尽くすものではなく、特殊相対性理論の「最も肝心な点」のみを表現するものに過ぎないよ。
さて、その悟りとは如何に?
それは「時間と空間を切り離すことは出来ない、時間と空間は一体となって時空を形成している」というものです。
特殊相対性理論の要点はこれに尽きます。
まず、空間に着目してみましょうか?
静止している人が x 軸の原点 x=0で時刻0に一発、時刻1に次の一発、拳銃を発砲したとしましょう。
これを運動している人が見ると、すなわち x 軸に重なったまま運動する x' 軸を用いて測定すると、2つの発砲は「異なる」位置( x' 座標)で起こっている事が分かります。
つまり、ある人にとって「同じ」位置で起こったと見なされる2つの事象が、もし「異なる」時刻に起こったならば、別の人にとっては「異なる」位置で起こったと見なされるわけです。
これを私は「時間が空間に混ざり込む」と言います。
数学的にはローレンツ変換の式の中の x' についての式の右辺に x だけでなく t が現れることが「時間が空間に混ざり込む」ことです。
アインシュタイン以前からこの事実は認められていたはずです。
「時間と空間を切り離すことが出来ない」と主張するためには「時間が空間に混ざり込む」だけでは不十分で、これに加えて「空間が時間に混ざり込む」ことが必要です。
すなわち、静止している人が観測して x 軸上の「異なる」2つの位置で異なる人が「同時に」拳銃を発砲したという結果が得られた場合、それを x' 軸に固定された時計で測定すると2つの発砲事象は「異なる」時刻に起こったものとして観測される、ことが必要です。
アインシュタイン以前には、「同時」に起こった事象は誰が見ても「同時」に起こった事象だ、と考えられていました。
これを否定し「空間の時間への混ざり込み」を主張するのがアインシュタインの特殊相対性理論です。
数学的にはローレンツ変換の式の中の t' についての式の右辺に t だけでなく x が現れることが「空間の時間への混ざり込み」を表しています。
以上がアインシュタインの特殊相対性理論の「最も肝心な部分」です。
要約すると、アインシュタインの特殊相対性理論の考え方の最も肝心な特徴は「ローレンツ変換によって、空間は時間に混ざり込み、かつ、時間は空間に混ざり込む、故に空間と時間を切り離して考えることは出来ない、両者は一体となって時空を形成する、と考えなくてはいけない」と主張する点です。