
since 2003
イレコナビ サイトマップ
ローレンツ収縮、および運動している時計の遅れ
このページでは特殊相対性理論で言うところの「運動物体が運動方向に縮むこと(ローレンツ収縮)」および「運動している時計が遅れること」について説明します。
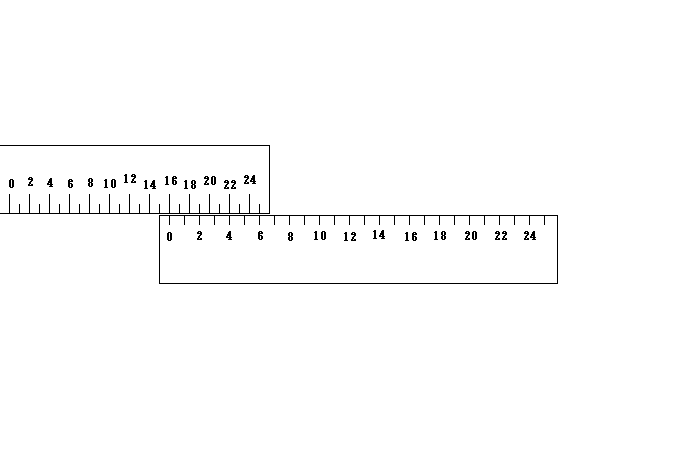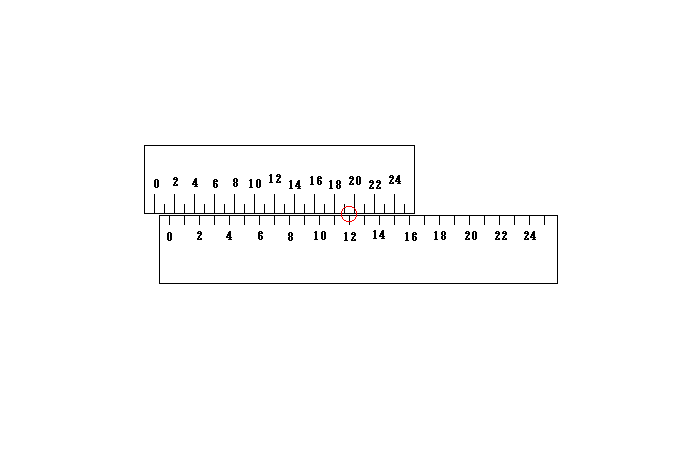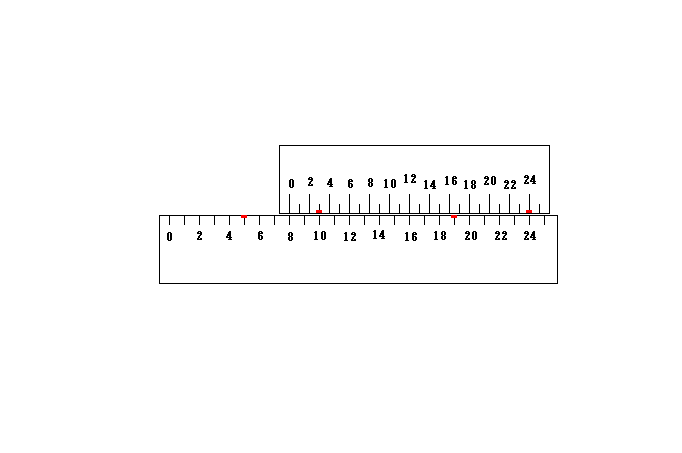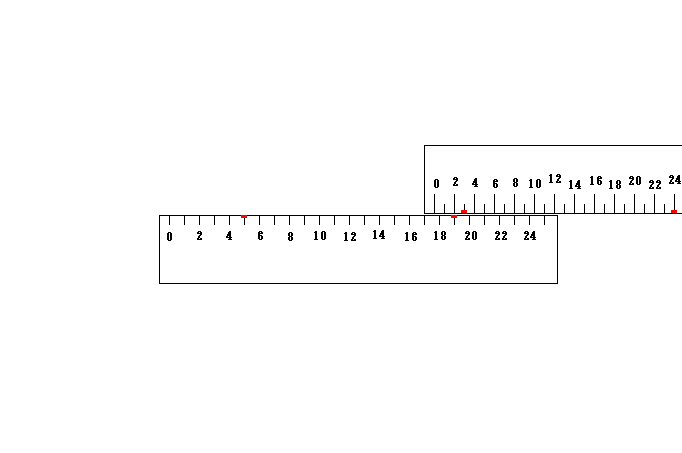
まずは下図をご覧下さい。
上の物差しと下の物差しは全く同じものです。
下の物差しは静止しており、上の物差しは右向きに一定の速度で運動してますね。
そのため上の物差しは運動方向に収縮しています。
さて、下の物差しによって上の物差しの点3から点24までの長さを測ることにしましょう。
ポイントは「同時性」です。
御覧のように同時性の保証には、光が同じ距離を進むのにかかる時間は向きによらず一定であるという事実を用います。
下図においては同時性保証用の光は赤円で示されており、上の物差しの点20が下の物差しの点12に一致した瞬間にその点から全方向にパルス状に放射されます。
この光は右側においては上の物差しの点24が下の物差しの点19に一致した瞬間にその点に丁度到達し、左側においては上の物差しの点3が下の物差しの点5に一致した瞬間に、その点に丁度到達します。
ところが光の発射地点12から下の物差しの点5までの距離と下の物差しの点19までの距離は全く同じです。
であるから、光が下の物差しの点5に到着する時刻と下の物差しの点19に到着する時刻は一致しなくてはいけません。
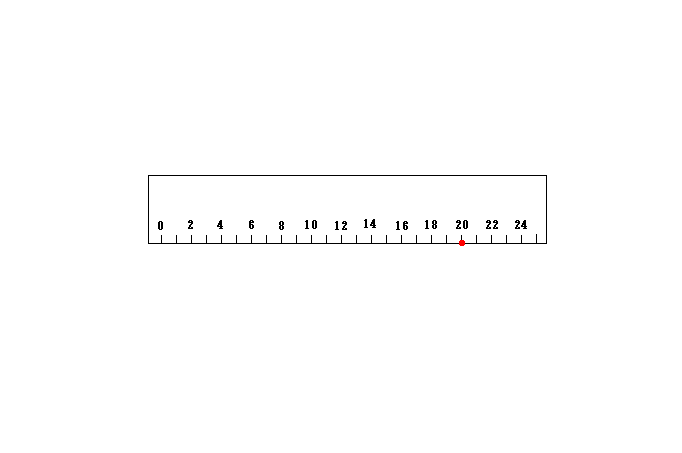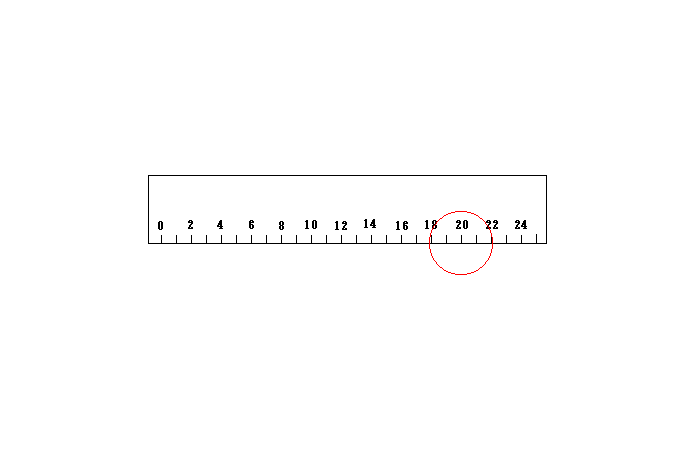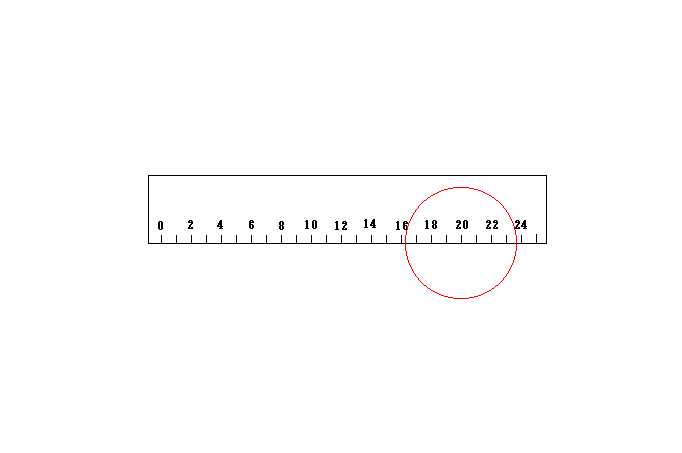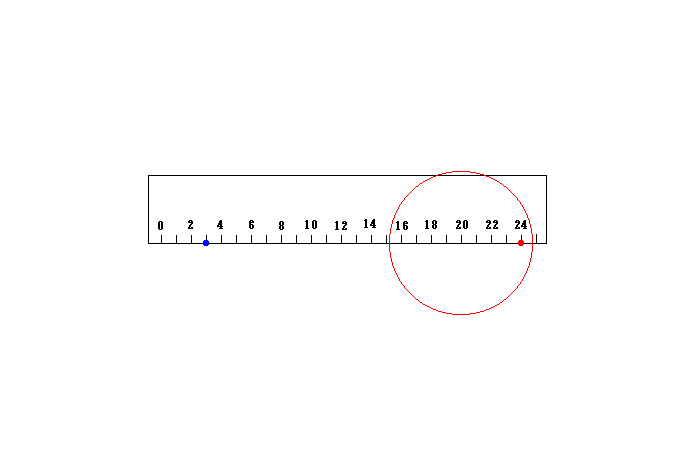
したがって上の物差しの点24が下の物差しの点19に一致する時刻と上の物差しの点3が下の物差しの点5に一致する時刻は一致することになります。
であるならば、上の物差しの点3から点24までの長さは、下の物差しで測れば19-5=14であると考えることが出来ます。
この値は24-3=21よりも小さく、確かにローレンツ収縮が起きています。
以上は下の物差しに固定された観測者が観測した場合の話です。
特殊相対性理論の発見法的指導原理の一つは「光速不変の原理」でした。
これは下の物差しに固定された観測者が観測する光速と上の物差しに固定された観測者が測定する光速が等しいという事を主張する原理です。
まず、下図から分かる様に点20から発射された光が点3と点24に同時に到着しないことが指摘できます。
下の物差しに固定された観測者が見ればこれらは同時に起こる事象なのでした。
この食い違いを指して「同時刻の相対性」と言います。
次に空間の1点(上の物差しの点20、下の物差しの点12)から発射された光が後に別の空間の1点(上の物差しの点24、下の物差しの点19)に到達するまでの時間を、上の物差しに固定された観測者が測定すると y であったとし、下の物差しに固定された観測者が測定すると w であったとします。
さらに光速を c とすると、cy=24-20=4 , cw=19-12=7となり y<w であることが分かります。
これが「運動する時計の遅れ」です。
しかしこれでは、宇田が最初から上の物差しを縮めて描いたからこういう結果が出て来たんだ、という批判を受けます。
そこで話を一般的にするために、光が下の物差しの点19に達した瞬間にその点に一致する上の物差しの点を表す数をBとし、光が下のもの差しの点5に達した瞬間にその点に一致する上の物差しの点を表す数をAとします。
上の図から明らかなようにB-20<20-Aです。
また、光が発射されてから上の物差しの点Aに到達するまでの時間を上の物差しに固定された時計で計った結果は x だったとし、光が発射されてから上の物差しの点Bに到達するまでの時間を上の物差しに固定された時計で計った結果は y だったとし、光が発射されてから下の物差しの点5に到達するまでの時間を下の物差しに固定された時計で計った結果は z だったとし、光が発射されてから下の物差しの点19に到達するまでの時間を下の物差しに固定された時計で計った結果は w だったとします。
すると、以下の式が全て成り立ちます。
cx=20-A , cy=B-20 , cz=12-5=7 , cw=19-12=7 ,
B-20<20-A
従ってB-A=19-5=14 , x=z , y=wの3つが全て成り立つことはあり得ません。
なぜなら
x=z , y=w を cx=20-A , cy=B-20に代入すると
cz=20-A , cw=B-20を得、
これに cz=12-5=7 , cw=19-12=7を代入すると、
7=20-A , 7=B-20故にA=13 , B=27となり、
B-20<20-Aに違反するからです。
これで「ローレンツ収縮」と「運動する時計の遅れ」の両方を同時に否定する事は出来ない、という事を「光速不変の原理」から導いたことになるが、また機会があったら「ローレンツ収縮」と「運動する時計の遅れ」が両方とも成り立つんだって事を説明してあげるかもしれない。
いずれにしても特殊相対性理論は4次元空間上のローレンツ変換に終始するものではない。
ニュートン力学の運動方程式を修正して相対論的運動方程式を書き表したり、電磁場を2階のテンソル場としてマックスウェルの電磁場方程式をローレンツ変換に対する共変性が明白な形に書き直したりするのが本論だ。
その際には今回私がやったような図解は不可能になる。
図が無くては分からない様ではマダマダだ。
早く、数式を理解して使いこなせるようになろうね。
そこへ後からマクスウェルの電磁気学が参入して来た。
アインシュタインの通ってた大学ではニュートン力学が教えられ新興のマクスウェル電磁気学はまだ教えられていなかった。
アインシュタインの偉いところは、そのマクスウェル電磁気学の重要性を認め、それを独学でマスターしたことだ。
さて特殊相対性理論成立以前には、ニュートン力学の運動方程式は全ての慣性系(静止しているかまたは回転せず一定の向きに一定の速さで運動し続ける座標系)で同じ式にならなくてはいけない、と考えられていた。
これを「ガリレイの相対性原理」と言い、その時に用いられる慣性系間の関係を表す変換式を「ガリレイ変換」と呼ぶ。
その当時はガリレイ変換の下でマクスウェル電磁気学の方程式が変わってしまうことがマクスウェル電磁気学の欠点の一つだと考えられていた。
マクスウェル電磁気学は電磁場に対する理論であり光は電磁場であるからマクスウェル電磁気学を使って光の速さを計算することが出来る。
慣性系ごとにマクスウェル電磁気学の方程式が変わるということは慣性系ごとに光の速さが変わるということだ。
もしどの慣性系を基準にしてもマクスウェル方程式が同じになるならば動いている人が見ても止まってる人が見ても光の速さは同じだということになる。
そのかわり、そういう結果が導き出されるような慣性系間の関係を表す関係式(これをローレンツ変換と呼ぶ)を採用すると、今度はニュートン力学の方程式が慣性系ごとに変わってしまう。
全ての慣性系で方程式が同じになることを要請するのが「相対性原理」と呼ばれる原理だ。
正しい物理法則は相対性原理に従わなくてはいけないと当時も考えられていた。
そこで次の選択を迫られる事になる。
「ニュートン力学が間違っててマクスウェル電磁気学が正しいのか、マクスウェル電磁気学が間違っててニュートン力学が正しいのか、どちらなのか?」
アインシュタイン以外のほとんどの人は、正統派ニュートン力学大司教様のおっしゃることの方が、いかがわしい新興マクスウェル電磁気学教の言うことより正しいに決まってると考えた。
しかしアインシュタインは違ってた。
彼はエルンスト・マッハの「ニュートン力学批判」の影響を受けるなどしてニュートン力学を絶対だとは思っていなかった。
そしてアインシュタインは「ニュートン力学が間違っててマクスウェル電磁気学が正しい、慣性系間の関係を表す変換式はガリレイ変換ではなくローレンツ変換である、と考える」という選択をした。
というわけなんだ。
その選択が正しいこと、を裏付ける実験として最も有名で決定的なものが「マイケルソン・モーレーの実験」と呼ばれるものだ。
ちゃんと実験によって裏付けられてるんだよ、アインシュタインの理論は。
悪い。
チョッと話を面白く書き過ぎた。
本当は、マイケルソン・モーレーの実験が行なわれた時代には、「光」は「エーテル」という物質を「媒質」とする波動だと考えられていた。
「媒質」って分かるだろ?
僕たちが日常生活において聞く「音」の「媒質」は「空気」だ。
したがって当時は、マクスウェル方程式はエーテルに固定された観測者から見て成り立てば良いだけであって、エーテルに対して運動している観測者(その観測者から見ればエーテルの風が吹いている様に見える)から見て成り立つ必要は無かったんだ。
マイケルソン・モーレーの実験結果は「エーテルの風は吹いていない」事を示すものだった。
それ以外の解釈を無理矢理にこじつける学者も居た。
が、普通は「エーテルの風は検出されなかった」と解釈する。
地球は自転・公転してるんだからエーテルの中を運動してるわけで、地球に固定された人から見ればエーテルの風が検出されるはずだ。
そこでアインシュタインは「エーテルは存在しない」という結論を下したわけだ。
エーテルが存在しないとなると「エーテルに対して静止している」という立場もなくなることになり、全ての慣性系が光(電磁場)を支配する法則の見地から見て同等であることになる。
だからマクスウェル方程式は全ての慣性系で同じでなくてはいけないことに成るんだ。
すると上記した様に慣性系間を結ぶ関係式は「ローレンツ変換」だってことになる。
こっちが本当だからね。
悪かったなあ。