
since 2003
イレコナビ サイトマップ
媒質に対する波の速さを V とする。
波源の振動数をνとする。
媒質の速度は観測者から波源に向かう向きに v だ、とする。
(媒質の風が波源から観測者に向かって吹いている場合には v < 0 と考えるだけで良い)
波源の速度は観測者から離れる向きに u だ、とする。
観測者の速度は波源に近付く向きに U だ、とする。

すると、ワンパターンの式は、次のように書ける。
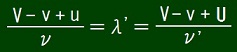
これより、ν' とλ' が求まる。
---
媒質の風が吹いていなくて、観測者が静止していて、波源のみが運動している場合は v = 0 and U = 0 の場合です。
媒質の風が吹いていなくて、波源が静止しており、観測者のみが運動している場合は v = 0 and u = 0 の場合です。
---
媒質の風が吹いており、波源も観測者も運動している場合(このページで説明されている場合)のワンパターンの式が、
v → 0, U → U - v, u → u - v
という置き換えに対して不変である事は、相対性原理(アインシュタインのではないけれど)の成立を意味します。
媒質と一緒に運動している観測者が見ると、
(媒質の速度) = 0, (観測者の速度) = U - v, (波源の速度) = u - v
ですが、この観点でもワンパターンの式が成り立たねばならぬ、とするのが相対性原理だからです。